Wektory w kosmosie Jak wykres, aplikacje, ćwiczenia

A wektor w przestrzeni Wszystko to jest reprezentowane przez układ współrzędnych podany przez X, I I z. Prawie zawsze samolot Xy Jest płaszczyzną powierzchni poziomej i osi z reprezentuje wysokość (lub głębokość).

Kartezjańskie osie współrzędnych pokazane na rycinie 1, dzielą przestrzeń na 8 obszarów zwanych Octaczniki, analogiczne do sposobu, w jaki osie X - I Podziel samolot na 4 ćwiartki. Następnie będziemy mieli 1 Octant, 2. Ocanto i tak dalej.

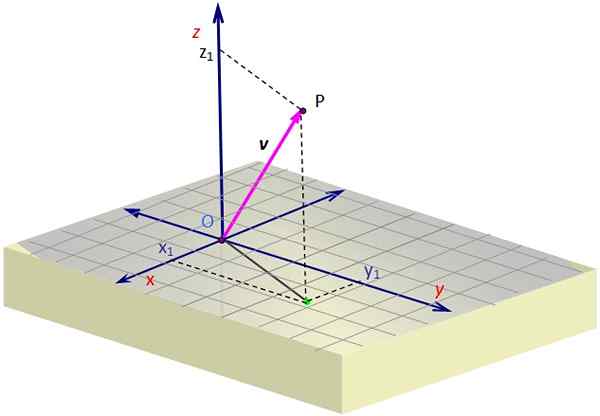
Rysunek 1. Wektor w przestrzeni. Źródło: Self Made.

Rycina 1 zawiera reprezentację wektora v w kosmosie. Wymagana jest pewna perspektywa, aby stworzyć iluzję trzech wymiarów na płaszczyźnie ekranu, który osiąga się poprzez rysowanie ukośnego widoku.

Aby wykres wektor 3D, musisz pomóc w kropkowanych liniach, które określają współrzędne projekcji lub „cienia” siatki v Nad powierzchnią x-i. Ta projekcja zaczyna się w O i kończy się w zielonym punkcie.

Po tym musisz kontynuować przez pionową do wysokości (lub głębokości) niezbędną zgodnie z wartością z, Dopóki nie dojdziesz do P. Wektor jest pobierany z O i kończące się P, który w przykładzie znajduje.

[TOC]

Aplikacje

Wektory w przestrzeni są szeroko stosowane w mechanice i innych gałęziach fizyki i inżynierii, ponieważ otaczające nas struktury wymagają geometrii w trzech wymiarach.

Wektory pozycyjne w przestrzeni są używane do pozycjonowania obiektów w odniesieniu do nazywanego punktu odniesienia pochodzenie ALBO. Dlatego są również niezbędnymi narzędziami w nawigacji, ale to nie wszystko.

Może ci służyć: fale elektromagnetyczne: teoria Maxwella, typy, cechy

Siły działające na struktury takie jak śruby, podporki, kable, rozpórki i inne są wektorami i są zorientowane w przestrzeni. Aby znać jego wpływ, konieczne jest znanie twojego adresu (a także punktu aplikacji).

I często kierunek siły jest znany z dwóch punktów w przestrzeni, która należą do jej linii działania. W ten sposób siła to:

F = F Lub

Gdzie f jest wielkością lub modułem siły i Lub Jest to wektor jednostkowy (moduł 1) skierowany wzdłuż linii działania F. 

Notacja wektora 3D i reprezentacje

Przed rozwiązaniem niektórych przykładów zapis wektorów 3D zostanie krótko przejrzany.

W przykładzie na rycinie 1 wektor V, którego punkt pochodzenia pokrywa się z pochodzeniem lub którego zakończenie jest punktem P, ma współrzędne X I z pozytywny, podczas gdy koordynuje I To jest negatywne. Te współrzędne to: X₁, I₁, z₁, które są dokładnie współrzędnymi p.

Więc jeśli mamy wektor powiązany z pochodzeniem, to znaczy, którego punkt początkowy pokrywa się z O, bardzo łatwo jest wskazać jego współrzędne, które będą te z punktu ekstremalnego lub p. Aby rozróżnić punkt od wektora, użyjemy najnowszych odważnych liter i nawiasów, takich jak ten:

v = < x₁, I₁, z₁ >

Podczas gdy punkt P jest oznaczony nawiasami:

P = (x₁, I₁, z₁)

Kolejna reprezentacja korzysta z wektorów jednostkowych Siema, J I k które definiują trzy kierunki przestrzeni w osiach X, I I z odpowiednio.

Te wektory są prostopadłe do siebie i tworzą Baza ortonormalna (Patrz Rysunek 2). Oznacza to, że wektor 3D może być napisany jako:

Może ci służyć: pofalowany ruch: cechy, rodzaje fal, przykłady

v = v_X Siema + v_I J + v_z k

Kąt i dyrektorzy wektora Cosenos

Rycina 2 pokazuje także reżyserów γ kąt₁, γ₂ i γ₃ niż wektor v odpowiednio z osiami X, I I z. Znając te kąty i wielkość wektora, jest to całkowicie ustalone. Ponadto cosinus dyrektorów spełniają następujący związek:

(cos γ₁)² + (cos γ₂)² + (cos γ₃)² = 1

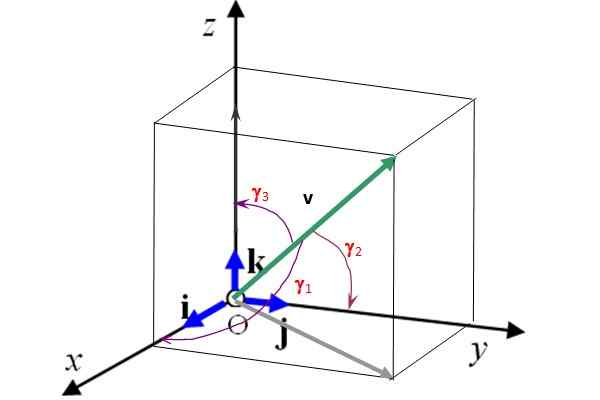Rysunek 2. Wektory jednolitowe I, J i K, określają 3 preferencyjne kierunki przestrzeni. Źródło: Self Made.

Rozwiązane ćwiczenia

-Ćwiczenie 1

Na rycinie 2 kąty γ₁, γ₂ i γ₃ niż wektor v formularza modułu 50 z osi współrzędnych to odpowiednio: 75.0º, 60.0º i 34.3. Znajdź komponenty kartezjańskie tego wektora i reprezentuj go w kategoriach wektorów jednostkowych Siema, J I k.

Rozwiązanie

Projekcja wektora v na osi X jest v_X = 50 . Cos 75º = 12.941. Podobnie projekcja v na osi I jest v_I = 50 cos 60 º = 25 i na koniec na osi z jest v_z = 50. cos 34.3rd = 41.3. Teraz v można wyrazić jako:

v = 12.9 Siema + 25.0 J + 41.3 k

-Ćwiczenie 2 

Znajdź napięcia w każdym z kabli, które trzymają wiadro figury, która jest w równowadze, jeśli ciężar wynosi 30 n.

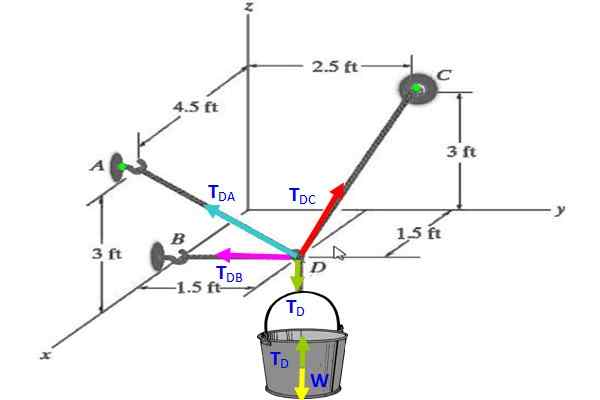Rysunek 3. Schemat napięć do ćwiczeń 2.

Rozwiązanie

Na wiadrze schemat wolnego ciała wskazuje T_D (zielony) kompensuje wagę W (żółty), dlatego t_D = W = 30 n.

W węzłach wektor T_D  Jest skierowany w pionowo, zatem:

T_D = 30 (-k) N.

Aby ustalić pozostałe napięcia, musisz wykonać następujące kroki:

Krok 1: Znajdź współrzędne wszystkich punktów

A = (4.5; 0; 3) (A jest na płaszczyźnie ściany X-Z)

B = (1.5; 0; 0) (B znajduje się na osi x)

Może ci służyć: adres (fizyczny)

C = (0, 2.5, 3) (C jest na płaszczyźnie ściany i z)

D = (1.5; 1.5; 0) (D znajduje się na płaszczyźnie poziomej  x-i)

Krok 2: Znajdź wektory w każdym kierunku, odejmując współrzędne końca i początek

Daje =

DC =

Db =

Krok 3: Oblicz moduły i wektory jednostkowe

Wektor jednostkowy jest uzyskiwany przez wyrażenie: Lub = R / r, z R (odważne) będąc wektorem i r (bez odważnego) moduł wspomnianego wektora.

DA = (3² + (-1.5)² + 3²)^½ = 4.5; Dc = (-1.5) ² + 1² + 3²)^½ = 3.5

Lub_Daje = 4.5 =

Lub_DC = 3.5 =

Lub_Db =

Lub_D =

Krok 4: Wyrażaj wszystkie napięcia jako wektory

T_Daje = T_Daje Lub_Daje = T_Daje

T_DC = T_DC Lub_{DC =}  T_DC

T_Db = T_Db Lub_Db = T_Db

 T_D = 30

Krok 5: Zastosuj stan równowagi statycznej i rozwiąż układ równań

Wreszcie warunek bilansu statycznego jest stosowany do wiadra, tak że suma wektora wszystkich sił na węzłach jest nieważna:

T_Daje + T_DC + T_Db + T_D = 0

Ponieważ napięcia są w przestrzeni, doprowadzi to do systemu trzech równań dla każdego komponentu (X, i i z) napięć.

0.67 t_Daje -0.43 t_DC + 0 t_Db = 0

-0.33 t_Daje + 0.29 t_DC - T_Db = 0

0.67 t_Daje + 0.86 t_DC +0 t_Db - 30 = 0

Rozwiązaniem jest: t_Daje = 14.9 N; T_Daje = 23.3 N; T_Db = 1.82 n

Bibliografia

1. Bedford, 2000. DO. Mechanika inżynierii: statyczne. Addison Wesley. 38-52.
2. Figueroa, zm. Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka.31-68.
3. Fizyczny. Moduł 8: wektory. Odzyskane z: frtl.Utn.Edu.ar
4. Hibbeler, R. 2006. Mechanika inżynierów. Statyczny. 6. edycja. Continental Editorial Company. 15-53.
5. Wektor kalkulatora dodania. Odzyskane z: 1728.org