Co to jest dolina w fizyce? (Z przykładami)

On Dolina w fizyce Jest to wyznanie stosowane w badaniu zjawisk pofalowanych, aby wskazać najniższą lub niższą wartość fali. Zatem dolina jest uważana za wklęsłość lub depresję.

W przypadku fali okrągłej utworzonej na powierzchni wody, gdy spadnie kropla lub kamień, zagłębienia są dolinami falowymi, a guzki są grzbietami.

Rysunek 1. Doliny i grzbiety na fali okrągłej. Źródło: Pixabay

Innym przykładem jest fala wygenerowana w napiętej linie, z których jeden z końca jest oscylowany pionowo, podczas gdy drugi pozostaje ustalony. W tym przypadku wytwarzana fala jest propagowana z pewną prędkością, ma kształt sinusou.

Poprzednie przykłady odnoszą się do fal krzyżowych, ponieważ doliny i grzbiety są poprzeczne lub prostopadłe do kierunku propagacji.

Jednak tę samą koncepcję można zastosować do fal podłużnych, takich jak dźwięk w powietrzu, których oscylacje występują w tym samym kierunku propagacji. Tutaj doliny fali będą miejsca, w których gęstość powietrza jest minimalna, a grzbiety, w których powietrze jest gęste lub sprężone.

[TOC]

Parametry fali

Nazywana jest odległość między dwiema dolinami lub odległością między dwoma grzbietami długość fali i oznacza Z greckim tekstem λ. Ten sam punkt fali przechodzi od bycia w dolinie do bycia grzebieniem, gdy oscylacja się rozprzestrzenia.

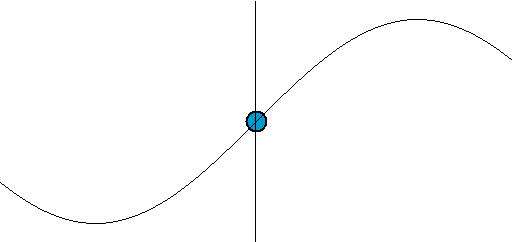Rysunek 2. Oscylacja fali. Źródło: Wikimedia Commons

Czas, który upływa z doliny-cresto-valle, w ustalonej pozycji nazywa się Okres oscylacji I ten czas jest oznaczony kapitałem T: T. 

Może ci służyć: Andromeda: odkrycie, pochodzenie, cechy, struktura

W czasie okresu T Fala rozwija długość fali λ, Dlatego mówi się, że prędkość v z którym postępuje fala, to:

V = λ / t

Pionowa separacja lub odległość między doliną a grzbietem fali jest dwa razy większy od zakresu oscylacji, to znaczy odległość od doliny do środka oscylacji pionowej jest amplituda a fali.

Doliny i grzbiety na fali harmonicznej

Fala jest harmonijna, jeśli jej kształt jest opisany przez funkcje matematyczne zatoki lub cosinus. Ogólnie rzecz biorąc, fala harmoniczna jest napisana jako:

i (x, t) = a cos (k⋅x ± ± ω⋅t)

W tym równaniu zmienna I reprezentuje odchylenie lub przemieszczenie w odniesieniu do pozycji równowagi (y = 0) w pozycji X W chwili T.

Parametr DO Jest to amplituda oscylacji, zawsze pozytywna ilość reprezentuje odchylenie od doliny falowej do centrum oscylacji (y = 0). W fali harmonicznej spełnia się, że odchylenie I, Od doliny po herb jest to A/2.

Numer fali 

Inne parametry, które pojawiają się w wzorze fali harmonicznej, szczególnie w argumencie funkcji sinusoidalnej, są liczbą falową k i częstotliwość kątowa Ω.

Numer fali k jest związane z długością fali λ przez następujące wyrażenie:

K = 2π/λ

Częstotliwość kątowa

Częstotliwość kątowa Ω jest związane z okresem T Poprzez:

Ω = 2π/t 

Zauważ, że w argumencie funkcji zatoki ± ±, to znaczy, w niektórych przypadkach znak pozytywny jest stosowany, aw innych znak ujemny.

Może ci służyć: statyczne: historia, jakie badania, aplikacje, prawa

Jeśli fala, która rozprzestrzenia się w pozytywnym kierunku X, Wtedy jest to najmniej (-) znak, który należy zastosować. W przeciwnym razie, w fali, która rozprzestrzenia się w kierunku ujemnym, stosuje się znak dodatni (+).

Fala harmoniczna

Prędkość propagacji fali harmonicznej można zapisać na podstawie częstotliwości kątowej i liczby fali w następujący sposób:

V = ω/k 

Łatwo jest wykazać, że to wyrażenie jest całkowicie równoważne z tym, które wcześniej daliśmy, w zależności od długości fali i okresu.

Przykład dolin: lina tenmentu

Dziecko gra fale z liną sznurka ubrań, dla której uwalnia jeden koniec i sprawia, że ​​jest oscylowany ruchem pionowym z prędkością 1 oscylacji na sekundę.

Podczas tego procesu dziecko pozostaje w tym samym miejscu i porusza tylko ramię z góry do dołu i odwrotnie.

Podczas gdy dziecko generuje fale, jego starszy brat robi zdjęcie z telefonem komórkowym. Porównując rozmiar fal z samochodem zaparkowanym tuż za liną, zauważ, że pionowe separacja między dolinami i grzbietami jest taka sama jak wysokość okien samochodu (44 cm).

Na zdjęciu można również zauważyć, że oddzielenie dwóch kolejnych dolin jest takie samo między tylną krawędzią tylnych drzwi a przednią krawędzią drzwi przednich (2,6 m).

Funkcja fali harmonicznej dla liny

Z tymi danymi starszy brat zamierza znaleźć funkcję fali harmonicznej przyjmującą jako moment początkowego (t = 0) moment, w którym ręka jego młodszego brata była w najwyższym punkcie. 

Może ci służyć: promieniowanie ciepła (z przykładami)

Będzie to również oznaczać, że oś x zaczyna się (x = 0) w miejscu dłoni, z pozytywnym kierunkiem z przodu i przechodząc przez połowę oscylacji pionowej. Za pomocą tych informacji można obliczyć parametry fali harmonicznej:

Amplituda to połowa wysokości doliny do grzebienia, to znaczy:

A = 44 cm /2 = 22 cm = 0,22 m

Numer fali jest 

K = 2π/(2,6 m) = 2,42 rad/m

Gdy dziecko podnosi i obniża dłoń w czasie sekundy, wówczas częstotliwość kątowa będzie

Ω = 2π/(1 s) =  6,28 rad/s

Krótko mówiąc, formuła fali harmonicznej jest

i (x, t) = 0,22 m cos (2,42⋅x - 6.28⋅t)

Prędkość propagacji fali będzie

v = 6,28 rad/s/2.42 rad/m = 15,2 m/s

Pozycja dolin w linie

Pierwsza dolina po sekundzie rozpoczęcia ruchu dłoni będzie odległością D dziecka i przekazywane przez następujący związek:

i (d, 1s) = -0,22 m = 0,22 m cos (2,42⋅D - 6.28⋅1)

Co oznacza że 

cos (2.42⋅D - 6.28) = -1

To jest do powiedzenia 

2.42⋅D - 6.28 = -π 

2.42⋅D = π

D = 1,3 m (pozycja doliny najbliżej t = 1s)

Bibliografia

1. Giancoli, zm. Fizyka. Zasady z aplikacjami. 6. edycja. Prentice Hall. 80-90
2. Resnick, r. (1999). Fizyczny. Tom 1. Trzecie wydanie po hiszpańsku. Meksyk. Continental Editorial Company S.DO. c.V. 100-120.
3. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wydanie. Meksyk. Redaktorzy edukacyjni Cengage. 95-100.
4. Sznurki, fale stojące i harmoniczne. Odzyskane z: Newt.Phys.UNSW.Edu.Au

5. Fale i mechaniczne proste fale harmoniczne. Odzyskany z: PhysicsKey.com.