Koncepcja wariacji liniowej, przykłady, rozwiązywane ćwiczenia

Zmiana liniowa Występuje między dwoma wielkościami fizycznymi, gdy wykres ich reprezentujący jest linią prostą. Jest to równoważne potwierdzenie, że zmienne są w zależności od liniowej, tak że jeśli jeden z nich nazywamy to „y”, a drugą „x”, będą one powiązane wyrażeniem matematycznym:

y = MX + B

W tej wzorze M i B są liczbami rzeczywistymi. Wartość M reprezentuje nachylenie lub nachylenie linii - która jest zawsze stała - a B jest cięciem linii z osą pionową.

Liniowa zmienność jednej wielkości w odniesieniu do drugiej oznacza, że ​​jego wykres jest linią prostą. Źródło: Joulesergio/CC BY-S (https: // creativeCommons.Org/licencje/nabrzeże/4.0)

Każde zjawisko, które reaguje na zmienność liniową, ma różne nazwy dla zmiennych, jak zobaczymy w poniższych przykładach. Jednak matematyczna forma równania jest taka sama.

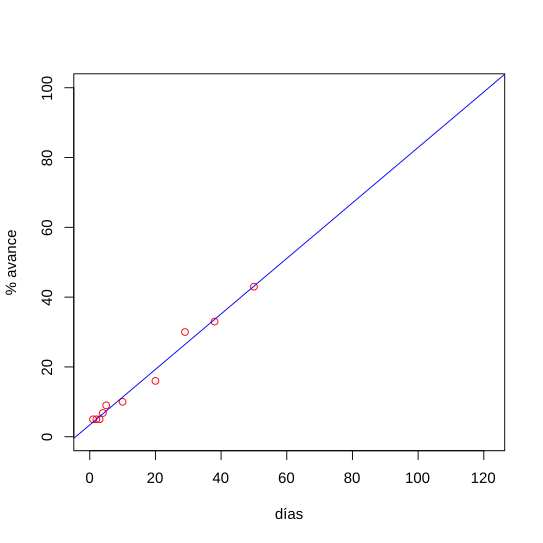
Eksperymentalnie można ustalić, jeśli istnieje liniowa zależność między dwoma wielkościami, pomiar par wartości (x, y).

Uzyskane punkty są graficzne w papierze milimetrowym i są obserwowane, jeśli mają one trend liniowy, to znaczy, jeśli istnieje linia, która odpowiednio dostosowuje się do danych eksperymentalnych.

Po pierwsze, linię tę można rysować wizualnie, ale za pomocą regresja liniowa Można je znaleźć analitycznie, wartości M i B linii, które najlepiej pasują do punktów eksperymentalnych.

[TOC]

Przykłady zmienności liniowej

Istnieje wiele naturalnych zjawisk, a także ustalone związki między wzorcami pomiarowymi, które są na przykład zmienności liniowej:

Prędkość w równomiernie zróżnicowanym ruchu prostoliniowym

Prędkość zależna od czasu v (t) telefonu komórkowego, który porusza się wzdłuż linii ze stałym przyspieszeniem i prędkością początkową v_albo  różni się od 0. Ten ruch jest znany jako równomiernie zróżnicowany ruch prostoliniowy A równanie prędkości to:

Może ci służyć: gęstość

v (t) = v_albo + NA

Rozszerzalność cieplna

Innym naturalnym zjawiskiem, którego zmienność jest liniowa, jest wzrost długości, który doświadcza pręta lub drutu po podgrzewaniu.

Rzeczywiście, gdy wzrośnie temperatura dowolnego obiektu, jego wymiary i wzrost ten zależy od zmiany temperatury δT Współczynnik rozszerzenia liniowego oznaczone grecką literą α:

L = L_albo + α δt

W tym wyrażeniu l jest końcową długością obiektu i L_albo to jego początkowa długość.

Pozycja telefonu komórkowego o stałej prędkości

Telefon komórkowy z prędkość stała zawsze porusza się w linii prostej. Jeśli linia prosta jest osą poziomą x, pozycja x (t) w dowolnym momencie jest podana przez:

x (t) = x_albo + Vt

Gdzie x_albo Jest to początkowa pozycja, v to prędkość, a T to czas. W ten sposób mówi się, że pozycja X zmienia się liniowo w zależności od czasu t.

Postawa osoby

Lekarze i antropologowie mogą oszacować postawę osoby, mierząc długość kości udowej.

Im wyższa osoba, tym dłuższe nogi mają, więc istnieją modele liniowe do przewidywania wysokości dorosłej osoby h (w calach), jeśli długość l (również w calach) jej kości udowej jest znana, zgodnie z równaniem:

H = 1.880⋅L + 32.010

Skale temperatury

Skale Celsjusza i Fahrenheita są używane codziennie do pomiaru temperatur. Ta ostatnia skala jest powszechnie używana w krajach rozpowszechnionych w języku angielskim. Istnieje równoważność przeniesienia się z jednego do drugiego:

F = (9/5) C + 32

Gdzie f jest temperaturą w stopniach Fahrenheita, a C jest temperaturą w stopniach Celsjusza.

Ciśnienie i głębokość

Ciśnienie bezwzględne P w płynie nieściśliwy, takim jak woda, którego stała gęstość wynosi ρ, zmienia się w zależności od głębokości h jako:

Może ci służyć: strzelanie poziome: cechy, wzory i równania, ćwiczenia

P = p_albo + ρgh

Gdzie p_albo Jest to ciśnienie na wolnej powierzchni cieczy. Jeśli ciecz jest w pojemniku otwartym na atmosferę, ciśnienie to jest po prostu ciśnieniem atmosferycznym P_bankomat, Możliwość pisania:

P = p_bankomat + ρgh

Ciśnienie atmosferyczne na poziomie morza wynosi około 101 kPa. Ten związek między P i H oznacza, że ​​ciśnienie wzrasta liniowo wraz z głębokością.

Ciśnienie odczuwane przez nurka zmienia się liniowo wraz z głębokością. Źródło: Ahmed Samy/Pexels.

Ćwiczenie rozwiązane

Koszt jazdy

Koszt miesięczny C obsługi samochodu obejmuje miesięczny koszt stały C_albo Plus koszty przebiegu lub przebiegu podróżowania co miesiąc. Kierowca zauważa, że ​​za miesiąc koszt zarządzania wyniósł 380 USD za 480 USD, a w następnym miesiącu 460 USD za 800 mil.

Niech ilość mil zostanie przewieziona miesięcznie przez kierowcę, wraz z dostarczanymi danymi, znajdź:

a) Liniowa zmienność między C i D.

b) ile kosztowałby samochód miesięcznie podczas podróży 1500 mil?

c) wykres C w porównaniu z D.

Rozwiązanie

Załóżmy, że zmienne mają związek podany przez:

C = c_albo + DO.D

Gdzie a i c_albo Są stałe do ustalenia. A jest nachyleniem linii, która graficznie reprezentuje związek między C i D. CO jest cięciem za pomocą osi pionowej, miesięczny koszt, który kierowca musi zapłacić za sam fakt, że samochód jest dostępny. Tutaj można uwzględnić na przykład koszty utrzymania i podatku.

Aby jednoznacznie określić linię, należy poznać jej nachylenie. W tym celu mamy punkty:

P₁: 480 mil, 380 USD

P₂: 800 mil, 460 USD

Te punkty, współrzędnych (d, c) lub (odległość, koszt) są analogiczne do punktów współrzędnych (x, y) płaszczyzny kartezjańskiej, jakie są nazwy. Stok na linię jest następnie podawany przez:

Może ci służyć: nachylona płaszczyzna

A = (c₂ - C₁)/(D₂ - D₁)

A = [(460 - 380) $ / (800 - 480) mil] = (1/4) $ / mile

Nachylenie linii reprezentuje koszt na milę, w ten sposób:

C = c_albo + DO.D = CO + (1/4).D

Aby określić podstawowy koszt C_albo To równanie jest zajęte, a jeden z punktów, które znamy, należy do niego, na przykład₁:

380 $ = c_albo + [(1/4) $ / mile] . 480 mil → 380 $ = c_albo + 120 USD

C_albo = 260 USD

Teraz możemy sformułować model zmienności liniowej, taki jak:

C = 260 + (1/4) D

Rozwiązanie b

Miesięczny koszt podróży 1500 mil wynosi:

C = 260 + (1/4) x 1500 $ = 635 USD

Rozwiązanie c

Wykres C jako funkcja D wynosi:

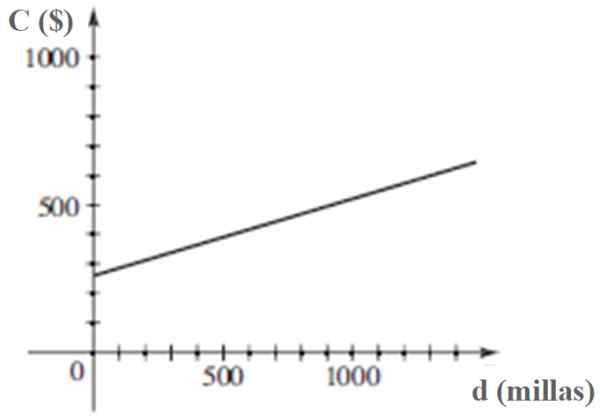Koszt C obsługi pojazdu jest funkcją liniową odległości przejechanej d. Źródło: Stewart, J. Przedłużanie.

Bibliografia

1. Baldor. 1977. Algebra podstawowa. Wenezuelskie wydania kulturalne.
2. Hoekenga, c. Równania liniowe w nauce. Odzyskane z: Visionlearning.com.
3. Hoffman, J. Wybór problemów z matematyką. Głośność 2.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
6. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.