Podstawowe twierdzenie o demonstracji arytmetycznej, zastosowaniach, ćwiczeniach

On Podstawowe twierdzenie arytmetyki Stwierdza, że ​​każda naturalna liczba większa niż 1 może zostać rozbita jako produkt liczb pierwszych - trzymanie niektórych - a ten formularz jest unikalny dla tej liczby, chociaż kolejność czynników może być inna.

Pamiętaj, że liczba pierwsza P Jest to ten, który przyznaje tylko jako pozytywne podziały i 1. Następujące liczby to kuzyni: 2, 3, 5, 7, 11, 13 i tak dalej, ponieważ są nieskończone. Numer 1 nie jest uważany za kuzyna za posiadanie jednego dzielnika.

Rysunek 1. Euclides (po lewej) wykazał podstawowe twierdzenie arytmetyki w swoich elementach książki (350 a.C.), A pierwsza pełna demonstracja jest spowodowana Carl F. Gauss (1777-1855) (po prawej). Źródło: Wikimedia Commons.

Ze swojej strony liczby, które nie spełniają powyższych, są wywoływane złożone liczby, Jako 4, 6, 8, 9, 10, 12, 14 ... Weźmy na przykład numer 10 i od razu widzimy, że można go rozbić jako produkt 2 i 5:

10 = 2 × 5

Zarówno 2, jak i 5 są rzeczywiście liczbami pierwszymi. Twierdzenie stwierdza, że ​​jest to możliwe dla dowolnej liczby N:

Gdzie p₁, P₂, P₃… P_R Są to liczby pierwszorzędne i k₁, k₂, k₃,... k_R Są liczbami naturalnymi. Tak, że liczby pierwotne działają jak cegły, z których przez mnożenie budowane są liczby naturalne.

[TOC]

Demonstracja podstawowego twierdzenia arytmetyki

Zaczyna się pokazać, że każda liczba może rozkładać się w podstawowych czynnikach. Być naturalną liczbą n> 1, kuzyn lub związek.

Na przykład, jeśli n = 2, można go wyrazić jako: 2 = 1 × 2, który jest kuzynem. W ten sam sposób kontynuujemy następujące liczby:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Kontynuujemy to, rozkładając wszystkie liczby naturalne, dopóki nie osiągniemy numeru N -1. Zobaczmy, czy możemy to zrobić z poniższą liczbą: n.

Jeśli n jest kuzynem, możemy go rozłożyć jako n = 1 × n, ale załóżmy, że n jest składane i ma dzielnika d, logicznie mniej niż n:

Może ci służyć: statystyka opisowa: historia, cechy, przykłady, koncepcje

1< d < n.

Tak N/D = P₁, z p₁ Liczba pierwsza, a następnie n jest napisane jako:

n = p₁.D

Jeśli D jest kuzynem, nie ma nic więcej do zrobienia, ale jeśli tak nie jest, istnieje liczba n₂ który jest dzielą D i mniej niż to: n₂ < d, por lo que d podrá escribirse como el producto de n₂ Dla innego kuzyna p₂:

d = p₂ N₂

Że zastępując oryginalną liczbę N: dałoby:

n = p₁ .P₂ .N₂

Teraz przypuśćmy, że n₂ Nie jest to również liczba pierwsza i piszemy go jako produkt liczby pierwszej p₃, dla jego dzielnicy₃, Takie, że n₃ < n₂ < n₁ < n:

N₂ = p₃.N₃ → N = P₁ P₂ P₃.N₃

 Powtarzamy tę procedurę skończoną liczbę razy, aż otrzymasz:

n = p₁.P₂.P₃ … P_R

Oznacza to, że możliwe jest rozkład wszystkich liczb całkowitych od 2 do liczby N, jako produkt liczb pierwszych.

Wyjątkowość rozkładu w podstawowych czynnikach

Sprawdźmy teraz, że z wyjątkiem kolejności czynników, ten rozkład jest wyjątkowy. Załóżmy, że możesz pisać na dwa sposoby:

n = p₁.P₂.P₃ … P_R = q_1.Q₂.Q₃… Q_S  (z r ≤ s)

Oczywiście Q₁, Q₂, Q₃… Są też liczbami pierwszymi. Jako p₁ podziel na (Q_1.Q₂.Q₃… Q_S) Następnie p₁ Jest równy dowolnym z „Q”, bez względu na Które, więc możemy powiedzieć, że P₁ = q₁. Dzielimy n między p₁ I dostajemy:

P₂.P₃ … P_R =_.Q₂.Q₃… Q_S

Powtarzamy procedurę, aby podzielić wszystko między p_R, Wtedy otrzymujemy:

1 = q_R+1… Q_S

Ale nie można dostać się do Q_R+1… Q_S = 1 Gdy r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Aplikacje

Jak powiedzieliśmy wcześniej, liczby pierwszorzędne reprezentują, jeśli chcesz, atomy liczb, ich podstawowych elementów. Tak więc podstawowe twierdzenie arytmetyki ma wiele zastosowań, najbardziej oczywiste: możemy łatwiej pracować z dużymi liczbami, jeśli wyrażamy je jako produkt mniejszych liczb.

Może ci służyć: liczby całkowitym

W ten sam sposób możemy znaleźć maksymalną wspólną wielokrotność (m.C.M.) i maksymalny wspólny dzielnik (m.C.D.;.

Ponadto liczby pierwszorzędne są wyjątkowo enigmatyczne. Wzór nie jest jeszcze w nich rozpoznany i nie można wiedzieć, jakie będą następujące. Największe, dopóki czasy zostały znalezione przez komputery i ma 24.862.048 cyfry, Chociaż nowe liczby pierwotne pojawiają się rzadziej za każdym razem.

Liczby Primo w naturze

Cycadas, Cycak lub Chicharras mieszkający na północno -wschodniej części Stanów Zjednoczonych pojawiają się w 13 lub 17 latach cykli. Oba są liczbami pierwszymi.

W ten sposób Chicharras unikają zbieżności z drapieżnikami lub konkurentami, które mają inne okresy urodzenia, ani różne odmiany Chicharra nie konkurują ze sobą, ponieważ nie pokrywają się w tym samym roku.

Rysunek 2. Magiczna Cicada del Este ze Stanów Zjednoczonych pojawia się co 13 lub 17 lat. Źródło: pxfuel.

Liczby Primo i zakupy online

Liczby Primo są używane w kryptografii do przechowywania szczegółów kart kredytowych przy zakupie zakupów online. W ten sposób dane, które kupujący przybywa dokładnie do sklepu, nie gubiąc się ani nie wpadając w pozbawione skrupułów ludzi.

Jak? Dane karty są kodowane w liczbie N, które można wyrazić jako produkt liczb pierwszych. Te liczby główne są kluczem, które ujawniają dane, ale są nieznane publiczności, można je od dekodować tylko w Internecie, do którego są skierowane.

Rozkład liczby na czynniki jest łatwym zadaniem, jeśli liczby są małe (widząc rozwiązywane ćwiczenia), ale w tym przypadku są one używane jako kluczowe liczby główne 100 cyfr, które poprzez ich pomnożenie daje znacznie większe liczby, których szczegółowy rozkład implikuje a Ogromna praca.

Może ci służyć: punktualne oszacowanie

Rozwiązane ćwiczenia

- Ćwiczenie 1

Rozkładaj 1029 na czynniki podstawowe.

Rozwiązanie

1029 jest podzielne przez 3. Znane jest, ponieważ dodając cyfry, suma jest wielokrotnością 3: 1+0+2+9 = 12. Ponieważ kolejność czynników nie zmienia produktu, możemy zacząć od tego:

1029 3

343

1029 = 3 × 343

Z drugiej strony 343 = 7³, Więc:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

A ponieważ zarówno 3, jak i 7 są liczbami pierwszymi, jest to rozkład 1029.

- Ćwiczenie 2

Czynnik Trinomialny x² + 42x + 432.

Rozwiązanie

Trinomial jest przepisywany w formie (x+a). (x+b) i musimy znaleźć wartości A i B, aby:

A+B = 42; Do.B = 432

Liczba 432 rozkłada się na czynniki podstawowe, a stamtąd jest wybrany przez Tanteo, odpowiednia kombinacja faktów dodanych do 42.

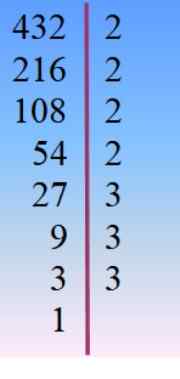
432 = 2⁴ × 3³ = 23³× 2³ = 2⁴× 3² × 3 =…

Stąd istnieje kilka możliwości napisania 432:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72… .

I wszystkie można znaleźć, łącząc produkty między czynnikami pierwszymi, ale aby rozwiązać proponowane ćwiczenie, jedyną odpowiednią kombinacją jest: 432 = 24 × 18 od 24 + 18 = 42, następnie:

X² + 42x + 432 = (x + 24). (x +18)

Bibliografia

1. Baldor, a. 1986. Praktyczna arytmetyka teoretyczna. Redaktor Cultural Company of American Texts s.DO.
2. BBC World. Ukryty kodeks natury. Źródło: BBC.com.
3. Od Leona, Manuel.Numery Primo: Strażnicy internetowi. Odzyskane z: blogów.20 minut.Jest.
4. Unam. Teoria liczb I: Podstawowe twierdzenie arytmetyki. Pobrano z: teoriagenumeros.Wikidot.com.
5. Wikipedia. Podstawowe twierdzenie arytmetyki. Odzyskane z: jest.Wikipedia.org.