Twierdzenie o istnieniu i wyjątkowości, przykłady i ćwiczenia

On Twierdzenie o istnieniu i wyjątkowości ustanawia niezbędne i wystarczające warunki dla równania różniczkowego pierwszego zamówienia, z danym warunkiem początkowym, aby mieć rozwiązanie i że to rozwiązanie jest również jedynym. 

Jednak twierdzenie nie podaje żadnej techniki ani wskazania, jak znaleźć takie rozwiązanie. Twierdzenie o istnieniu i wyjątkowości rozciągają się również na równania różniczkowe wyższego rzędu z warunkami początkowymi, które jest znane jako problem Cauchy.

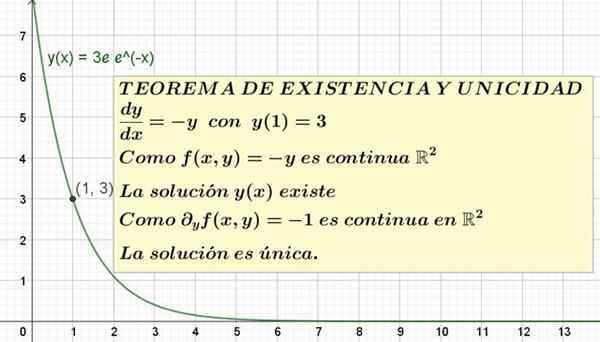
Rysunek 1. Pokazano równanie różniczkowe ze stanem początkowym i jego rozwiązaniem. Twierdzenie o istnieniu i wyjątkowości gwarantuje, że jest to jedyne możliwe rozwiązanie.

Formalne stwierdzenie twierdzenia o istnieniu i wyjątkowości jest następujące:

„Dla równania różniczkowego i '(x) = f (x, y) ze stanem początkowym i (a) = b,  istnieje co najmniej jedno roztwór w prostokątnym obszarze płaszczyzny Xy zawierający punkt (A, B), Tak f (x, y) Jest ciągły w tym regionie. I jeśli częściowa pochodna F w szacunku dla I: G = ∂f/ ∂y Jest ciągły w tym samym regionie prostokątnym, więc rozwiązanie jest unikalne w środowisku punktu (A, B) treść w regionie ciągłości F I G."

Przydatność tego twierdzenia leży najpierw, aby wiedzieć, jakie są regiony płaszczyzny XY, w których mogą istnieć rozwiązanie, a także wiedzieć, czy znaleziono rozwiązanie jest jedynym możliwym, czy też są inne. 

Zauważ, że w przypadku stanu unikalnego.

[TOC]

Demonstracja twierdzenia o istnieniu i wyjątkowości

Rysunek 2. Do Charlesa Émile Picard (1856–1941) Jedno z pierwszych demonstracji twierdzenia o istnieniu i wyjątkowości jest akredytowane. Źródło: Wikimedia Commons.

W tym twierdzeniu znane są dwie możliwe demonstracje, jedno z nich to demonstracja Charlesa Émile Picarda (1856–1941), a druga jest spowodowana Giuseppe Peano (1858–1932) opartą na pracach Augustina Louisa Cauchy'ego (1789-1857 ).

Może ci służyć: wektory współbieżne: cechy, przykłady i ćwiczenia

Należy zauważyć, że najjaśniejsze matematyczne umysły XIX wieku uczestniczyły w demonstracji tego twierdzenia, więc może być intuitu, że żadne z nich nie jest proste.

Aby formalnie zademonstrować twierdzenie, konieczne jest najpierw ustanowienie serii bardziej zaawansowanych koncepcji matematyki, takich jak funkcje typu Lipschitz, przestrzenie Banacha, Caratheodory i kilka innych twierdzeń o istnieniu, które uciekają.

Duża część równań różniczkowych, które są obsługiwane w fizyce, dotyczy ciągłych funkcji w obszarach zainteresowania, dlatego ograniczymy się do wykazania sposobu, w jaki twierdzenie jest stosowane w prostych równań.

Przykłady

- Przykład 1

Rozważ następujące równanie różniczkowe z warunkiem początkowym:

i '(x) = - y; z i (1) = 3

Czy istnieje rozwiązanie tego problemu? Czy to jedyne możliwe rozwiązanie?

Odpowiedzi

Po pierwsze, oceniane jest istnienie rozwiązania równania różniczkowego i że spełnia on również warunek początkowy. 

W tym przykładzie f (x, y) = - y Warunek istnienia wymaga wiedzy, czy  f (x, y) Jest ciągły w obszarze płaskim Xy zawierający punkt współrzędnej x = 1, y = 3.

Ale f (x, y) = -y To jest Powiązana funkcja, który jest ciągły w dziedzinie liczb rzeczywistych i istnieje w całym zakresie liczb rzeczywistych.

Dlatego stwierdza się, że f (x, y) jest ciągłe w r², Tak więc twierdzenie gwarantuje istnienie co najmniej jednego rozwiązania.

Wiedząc o tym, nadszedł czas, aby ocenić, czy rozwiązanie jest unikalne, czy też wręcz przeciwnie, jest więcej niż jeden. W tym celu konieczne jest obliczenie częściowej pochodnej F Dotyczące zmiennej I:

∂f/∂y = ∂ (-y)/∂y = -1

Więc G (x, y) = -1 która jest stałą funkcją, która jest również zdefiniowana dla wszystkich r² I jest tam również ciągły. Wynika z tego, że twierdzenie o istnieniu i wyjątkowości gwarantuje, że ten problem wartości początkowej ma unikalne rozwiązanie, chociaż nie mówi nam, co to jest.

Może ci służyć: wypukły wielokąta: definicja, elementy, właściwości, przykłady

- Przykład 2

Rozważ następujące pierwsze równanie różniczkowe Pierwsze Zamów z warunkami początkowymi:

i '(x) = 2√y; i (0) = 0.

Czy jest rozwiązanie i (x) dla tego problemu? Jeśli tak, ustal, czy jest jeden lub więcej niż jeden.

Odpowiedź

Rozważamy funkcję f (x, y) = 2√y. Funkcja F jest zdefiniowany tylko dla y≥0, Wiemy, że liczba ujemna nie ma prawdziwego korzenia. Oprócz f (x, y) Jest ciągły w górnej półplancie R²  w tym oś x, więc Twierdzenie o istnieniu i wyjątkowości gwarantuje Co najmniej jedno rozwiązanie w tym regionie.

Teraz warunek początkowy x = 0, y = 0 znajduje się na krawędzi regionu roztworu. Następnie bierzemy częściową pochodną f (x, y) w odniesieniu do y:

∂f/∂y = 1/√y

W takim przypadku funkcja nie jest zdefiniowana dla y = 0, dokładnie tam, gdzie jest warunek początkowy.

Co mówi nam twierdzenie? Mówi nam, że chociaż wiemy, że istnieje co najmniej jedno rozwiązanie, górna semiplane osi x, w tym osi x, ponieważ stan wyjątkowości nie jest spełniony, nie ma gwarancji, że istnieje jedno rozwiązanie.

Oznacza to, że może istnieć jedno lub więcej jednego rozwiązania w obszarze ciągłości F (x, y). I jak zawsze twierdzenie nie mówi nam, co może być.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Rozwiąż problem Cauchy'ego przykładu 1:

i '(x) = - y; z i (1) = 3. 

Znajdź funkcję y (x), która spełnia równanie różniczkowe i warunek początkowy.

Rozwiązanie

W przykładzie 1 ustalono, że problem ten ma rozwiązanie i jest również wyjątkowy. Aby znaleźć rozwiązanie, pierwszą rzeczą, którą należy zauważyć, jest to, że jest to pierwsze równanie różniczkowe zmiennych rozdzielonych, które jest napisane w następujący sposób:

Może ci służyć: Współczynnik odmiany: co to jest, do obliczeń, przykładów, ćwiczeń

dy /dx = - i → dy = -y dx

Dzielenie między obiema członkami i u, aby oddzielić zmienne, które mamy:

dy/y = - dx

Zastosowana jest nieokreślona całka obu członków:

∫ (1/y) dy = - ∫dx

Rozwiązywanie nieokreślonych całek to:

Ln (y) = -x + c

gdzie C jest stałą integracji, która jest określona przez warunek początkowy:

ln (3) = -1 + c, to znaczy, że c = 1 + ln (3)

Zastąpienie wartości C i reorganizacji to:

ln (y) - ln (3) = -x + 1

Stosowanie następującej właściwości logarytmów:

Różnica w logarytmach to logarytm ilorazowy

Poprzednie wyrażenie można przepisać w ten sposób:

LN (y/3) = 1 - x

Funkcja wykładnicza jest stosowana z obiema członkami w celu uzyskania:

Y / 3 = e^{(1 - x)}

Co jest równoważne:

 y = 3e e^-X

Jest to unikalne rozwiązanie równania i '= -y z y (1) = 3. Wykres tego rozwiązania pokazano na rycinie 1.

- Ćwiczenie 2

Znajdź dwa rozwiązania problemu podniesionego w przykładzie 2:

i '(x) = 2√ (y); i (0) = 0.

Rozwiązanie

Jest to również równanie oddzielnych zmiennych, które jest napisane różnicowo, pozostaje:

Dy / √ (y) = 2 dx

Pozostaje nieokreślona całka w obu członkach:

2 √ (y) = 2 x + c

Jak wiadomo y≥0 W regionie rozwiązania mamy:

y = (x + c)² 

Ale jako warunek początkowy x = 0, y = 0 musi być spełniony, stała c wynosi zero, a następujące rozwiązanie pozostaje:

i (x) = x².

Ale to rozwiązanie nie jest unikalne, funkcja y (x) = 0 jest również rozwiązaniem podniesionego problemu. Twierdzenie o istnieniu i wyjątkowości zastosowane do tego problemu w przykładzie 2 przewidziało już, że może istnieć więcej niż jedno rozwiązanie.

Bibliografia

1. Coddington, Earl A.; Levinson, Norman (1955), Theory of Ordinary Różnicowe równania, Nowy Jork: McGraw-Hill.
2. Encyklopedia matematyki. Twierdzenie Cauchy-Lipschitz. Odzyskane z: Encyclopediaofmath.org
3. Lindelöf, South L'A Zastosowanie Metode des A ocxroksations Aux Aux qéquations Diftérentielles Ordinaires du Premier Ordre; Compttes Rendus hebdomadaires des séances de l'Enc Acadequie des Sciences. Tom. 116, 1894, pp. 454-457. Odzyskane z: gali.BNF.Fr.
4. Wikipedia. Metoda kolejnych podejść Picarda. Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Twierdzenie Picard-Lindelöf. Odzyskane z: jest.Wikipedia.com.
6. Zill, d.1986. Podstawowe równania różniczkowe z aplikacjami.Prentice Hall.