Hiperboliczna definicja paraboloidów, właściwości i przykłady

A Hiperboliczny paraboloid Jest to powierzchnia, której ogólne równanie we współrzędnych kartezjańskich (x, y, z) spełnia następujące równanie:

(Do)² - (oraz b)² - Z = 0.

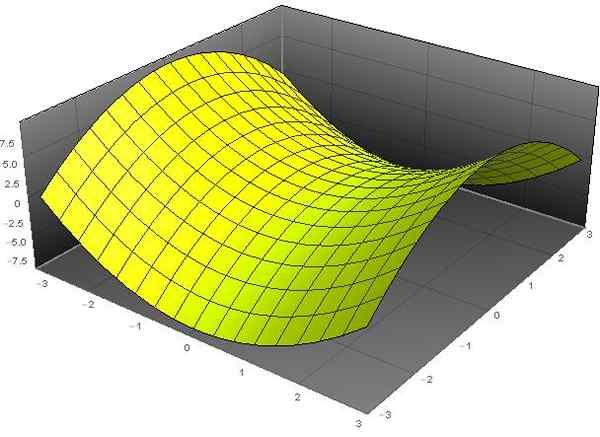
Nominacja „paraboloid” wynika z faktu, że zmienna Z zależy od kwadratów zmiennych x i y. Podczas gdy przymiotnik „hiperboliczny” wynika z faktu, że równanie hiperboli ma stałe wartości Z. Kształt tej powierzchni jest podobny do kształtu krzesła konnego.

Rysunek 1. Hiperboliczne paraboloid Z = x² - I². Źródło: f. Zapata przez Wolfram Mathematica.

[TOC]

Opis hiperbolicznego paraboloidu

Aby zrozumieć naturę hiperbolicznego paraboloidu, zostanie przeprowadzona następująca analiza:

1.- Konkretny przypadek zostanie pobrany a = 1, b = 1, to znaczy, że równanie kartezjańskie paraboloidów pozostaje jako z = x² - I².

2.- Są uważane za równoległe płaszczyzny do płaszczyzny ZX, czyli y = ctte.

3.- Z y = ctte to z = x² - C, który reprezentuje przypowieści z gałęzią i wierzchołkiem poniżej płaszczyzny XY.

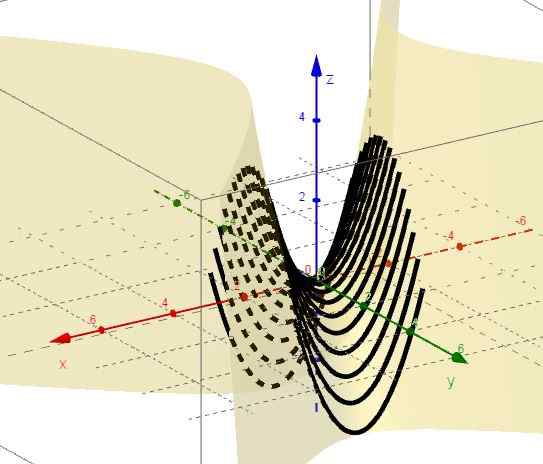Rysunek 2. Rodzina krzywych z = x² - C. Źródło: f. Zapata przez Geogebra.

4.- Z x = ctte to z = c - y², który reprezentuje przypowieści z gałęziami i wierzchołkami nad płaszczyzną XY.

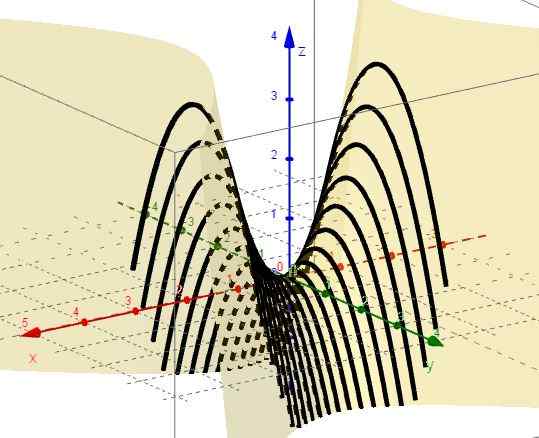Rysunek 3. Rodzina krzywych z = c - i². Źródło: f. Zapata przez Geogebra.

5.- Z Z = CTTE to c = x² - I², które reprezentują hiperbolę w płaszczyznach równoległych do płaszczyzny XY. Gdy C = 0 Istnieją dwie linie (A +45º i -45º w odniesieniu do osi x), które są przechwycone w początkowym płaszczyźnie XY.

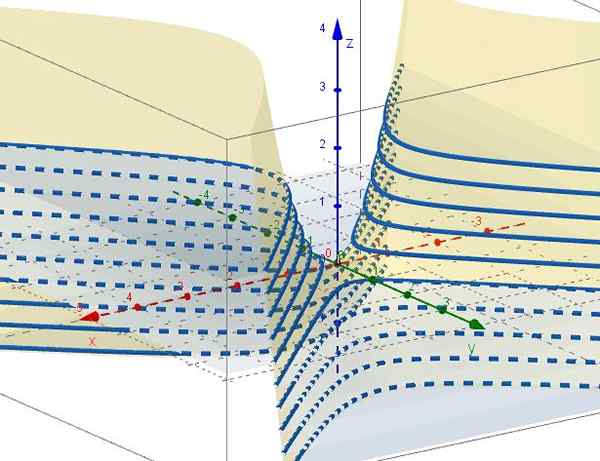Rysunek 4. Rodzina krzywych x² - I² = C. Źródło: f. Zapata przez Geogebra ..

Właściwości hiperbolicznych paraboloidów

1.- Cztery różne punkty w trójwymiarowej przestrzeni definiują jeden i tylko hiperboliczny paraboloid.

Może ci służyć: Limit właściwości (z przykładami)

2.- Hiperboliczny paraboloid to podwójnie regulowana powierzchnia. Oznacza to, że pomimo bycia zakrzywioną powierzchnią, dla każdego punktu hiperbolicznego paraboloidów dwie różne linie przechodzą całkowicie do hiperbolicznego paraboloidu. Druga powierzchnia, która nie jest płaszczyzną i jest podwójnie regulowana Rewolucja hiperboloid.

Właśnie to druga właściwość hiperbolicznego paraboloidu, która pozwoliła na szerokie użycie go w architekturze, ponieważ powierzchnia może być generowana z wiązek lub prostych sznurków.

Druga właściwość hiperbolicznego paraboloidu pozwala na jego alternatywną definicję: Jest to powierzchnia, którą można wygenerować przez prostą linię mobilną równoległą do stałej płaszczyzny i przecina dwie stałe linie, które służą jako przewodnik. Poniższy rysunek wyjaśnia tę alternatywną definicję hiperbolicznego paraboloidu:

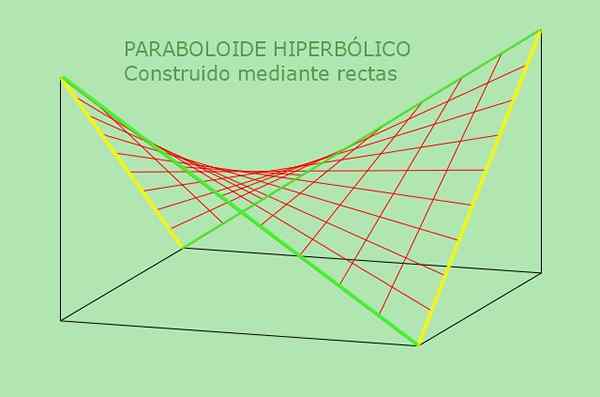Rysunek 5. Hiperboliczny paraboloid jest podwójnie regulowaną powierzchnią. Źródło: f. Zapata.

Rozwiązane przykłady

- Przykład 1

Wykazać, że równanie: Z = xy, odpowiada hiperbolicznemu paraboloidowi.

Rozwiązanie

Transformacja zostanie zastosowana w zmiennych x i y odpowiadających obrotowi osi kartezjańskich w odniesieniu do Z osi +45. Stare współrzędne x i y są przekształcane w nowe x 'e i' zgodnie z następującymi relacjami:

x = x ' - y'

y = x ' + i'

Chociaż współrzędna Z pozostaje taka sama, czyli z = z '.

Zastępując w równaniu z = x i mamy:

Z '= (x' - y ') (x' + y ')

Przy stosowaniu znaczącego produktu różnicy przez sumę równą różnicy kwadratów jest to:

Z '= x'² - I'²

co wyraźnie odpowiada definicji początkowo podanej hiperbolicznych paraboloidów.

Przechwycenie płaszczyzn równolegle do osi xy z hiperbolicznym paraboloidem z = x i określając równoboczne hiperboli, które mają asymptoty płaszczyzny x = 0 e y = 0.

Może ci służyć: Miletus taki twierdzenie

- Przykład 2

Określ parametry Do I B hiperbolicznego paraboloidu, który przechodzi przez punkty a (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) i D (2, -1, 32/9).

Rozwiązanie

Zgodnie z jego właściwościami cztery punkty w trójwymiarowej przestrzeni determinują pojedynczy hiperboliczny paraboloid. Ogólne równanie to:

Z = (x/a)² - (oraz b)²

Zastępujemy podane wartości:

Dla punktu A masz 0 = (0/a)² - (0/b)², równanie, które jest spełnione, niezależnie od wartości parametrów A i B.

Uzyskuje się zastępujący punkt B:

5/9 = 1/a² - 1 b²

Podczas gdy dla punktu C pozostaje:

32/9 = 4/a² - 1 b²

Wreszcie, dla punktu D jest uzyskiwane:

32/9 = 4/a² - 1 b²

Który jest identyczny z poprzednim równaniem. Krótko mówiąc, układ równań należy rozwiązać:

5/9 = 1/a² - 1 b²

32/9 = 4/a² - 1 b²

Odejmowanie drugiego równania pierwszego jest uzyskiwane:

27/9 = 3/a² co to implikuje² = 1.

Podobnie, drugie równanie czterokrotnego pierwszego odejmuje się, uzyskując:

(32-20)/9 = 4/a² - 4/a² -1 b² + 4/b²

To jest uproszczone jako:

12/9 = 3/b² ⇒ b² = 9/4.

Krótko mówiąc, hiperboliczny paraboloid, który przechodzi przez punkty A, B, C i D, ma równanie kartezjańskie podane przez:

Z = x² - (4/9) i²

- Przykład 3

Zgodnie z właściwościami hiperbolicznego paraboloidu, dwie linie, które są całkowicie zawarte w IT, przechodzą dla każdego punktu. W przypadku z = x^2 - y^2 Znajdź równanie dwóch linii, które przechodzą przez punkt P (0, 1, -1) wyraźnie należące do hiperbolicznego paraboloidu, tak że wszystkie punkty tych linii również należą do To samo.

Rozwiązanie

Korzystając z niezwykłego produktu różnicy w kwadratach, równanie hiperbolicznego paraboloidu można zapisać w następujący sposób:

Może ci służyć: czworobok: elementy, właściwości, klasyfikacja, przykłady

(x + y) (x - y) = c z (1/c)

Gdzie C jest stałą niezerową.

Równanie x + y = c z i równanie x - y = 1/c odpowiadają dwóch płaszczyzn z normalnymi wektorami N= y M=. Produkt wektorowy m x n = Kierunek przecięcia linii dwóch samolotów daje nam. Następnie jedna z linii, która przechodzi przez punkt P i należy do hiperbolicznego paraboloidu, ma równanie parametryczne:

= + t

Aby określić C, zastępujemy punkt P w równaniu x + y = c z, uzyskując:

C = -1

Podobnie, ale biorąc pod uwagę równania (x - y = k z) i (x + y = 1/k) masz równanie parametryczne linii:

= + s z k = 1.

Krótko mówiąc, dwie linie:

= + t y = + s

Są całkowicie zawarte w hiperbolicznym paraboloidach z = x² - I² Przechodząc przez punkt (0, 1, -1).

Jako czek Załóżmy, że t = 1 Co daje nam punkt (1,2, -3) na pierwszej linii. Musisz sprawdzić, czy jest to również na paraboloidach z = x² - I²:

-3 = 1² - 2² = 1 - 4 = -3

Co potwierdza, że ​​w efekcie należy do powierzchni hiperbolicznego paraboloidu.

Hiperboliczny paraboloid w architekturze

Rysunek 6. Oceanographic of Walencia (Hiszpania).Źródło: Wikimedia Commons.

Hiperboliczny paraboloid był używany w architekturze przez wielkich awangardowych architektów, w tym nazwiska hiszpańskiego architekta Antoni Gaudí (1852–1926), a szczególnie hiszpańskie również hiszpańskie félix candela (1910–1997) są szczególnie szczególnie.

Poniżej kilka prac opartych na hiperbolicznym paraboloidu:

-Kaplica Miasta Cuernavaca (Meksyk) Praca architekta Félixa Candela.

-Oceanographic of Valencia (Hiszpania), również autorstwa Félix Candela.

Bibliografia

1. Encyklopedia matematyki. Rządzona powierzchnia. Odzyskane z: Encyclopediaofmath.org
2. Llera Rubén. Hiperboliczny paraboloid. Odzyskane z: rubenllera.WordPress.com
3. Weisstein, Eric W. „Hiperboliczny paraboloid.”Z zasobów internetowych Mathworld-A Wolfram. Odzyskane z: Mathworld.Wolfram.com
4. Wikipedia. Paraboloida. Źródło: w:.Wikipedia.com
5. Wikipedia. Paraboloida. Odzyskane z: jest.Wikipedia.com
6. Wikipedia. Rządzona powierzchnia. Źródło: w:.Wikipedia.com