Jakie są trójkątne liczby? Właściwości i demonstracje

Jest znany jako Liczby trójkątne do sekwencji liczb, które są uzyskiwane przez wykonanie rozmieszczenia lub liczby punktów równobocznego trójkąta. Pierwsza z sekwencji to: 1, 3, 6, 10, 15, 21, ..

Pierwszy problem trójkątny to 1, drugi to 3, ponieważ uzyskuje się od dodania dwóch punktów do poprzedniego, aby utworzyć równoboczny trójkąt trzech elementów.

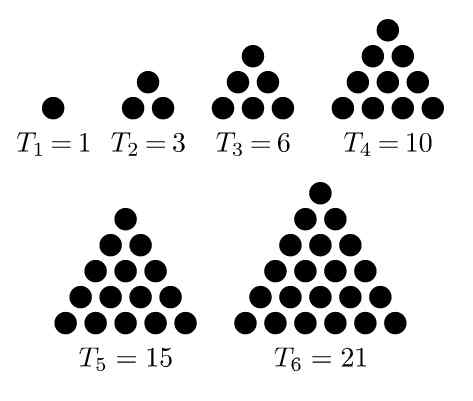
Rysunek 1. Sekwencja pierwszych sześciu trójkątnych liczb. Źródło: Wikimedia Commons. MelChoir/CC BY-SA (https: // creativeCommons.Org/licencje/by-sa/3.0)

Trzeci to 6, który pojawia się podczas dodawania trzech punktów do poprzedniego układu, tak że na stronę powstał trójkąt trzypunktowy. 10 sekwencji jest uzyskiwana przez dodanie kolejnego wiersza do poprzedniego układu, tak aby na stronę powstała trójkąt czteropunktowy.

Formuła, która pozwala znaleźć element N Z sekwencji trójkątnej znana przednia liczba trójkątna wynosi:

T_N = T_N-1 + N

Lista pierwszych sześciu trójkątnych liczb jest osiągana w ten sposób:

-Pierwszy: 1

-Drugi: 1 + 2 = 3

-Trzeci: (1 +2) + 3 = 3 + 3 = 6

-Pokój: (1 + 2 + 3) + 4 = 6 + 4 = 10

-Piąty: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15

-Szósty: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21

[TOC]

Właściwości liczb trójkątnych

1.- N-SIMO TN Trójkątna liczba trójkątnej sekwencji liczb to połowa n pomnożona przez n+1:

T_N = ½ n (n+1)

2.- Suma trójkątnej liczby N-ésimo z przednią trójkątną liczbą, to znaczy (n-1) -sheimo, jest podniesiona kwadratowa:

T_N + T_N-1= n²

3.- Różnica w trójkątnej liczbie n-mniej niż trójkątne n-isimo mniej jeden wynosi n:

T_N - T_N-1 = n

4.- Suma pierwszych liczb trójkątnych nazywa się liczbą czworościenną SN i jest równa szóstej części produktu pomnożonego przez (n + 1) i pomnożona przez (n + 2):

Może ci służyć: opodatkowanie

S_N= ⅙ n (n + 1) (n + 2)

5.- Każda naturalna liczba N jest wynikiem suma trzech trójkątnych liczb:

N = δ1 + δ1 + δ3

Ta ostatnia własność lub twierdzenie został odkryty przez wielkiego matematyka Carla Friedricha Gaussa w 1796 r., Który zdobył w swoim dzienniku, umieszczając grecki podziw Eureka! co to znaczy „Osiągnąłem to”.

To było to samo słowo użyte znacznie wcześniej przez greckie archimedes, kiedy określił pozorną wagę zanurzonego ciała.

W tym związku liczba zerowa jest traktowana jako trójkątna i może nastąpić powtórzenie.

Demonstracje

- Demonstracja 1

Udowodnić, że liczba trójkątna N-To jest:

T_N = ½ n (n+1)

Łatwo jest wydedukować poprzednią formułę, jeśli zdamy sobie sprawę, że możemy dodać tę samą liczbę punktów do trójkątnego układu, tworząc czworobok punktów.

Ponieważ całkowita liczba punktów rozmieszczenia w postaci czworoboku jest liczba wierszy N pomnożone przez liczbę kolumn (N+1), Wtedy układ trójkątny będzie miał tylko połowę punktów układu w postaci czworoboku.

Tutaj ilustruje na rycinie 2.

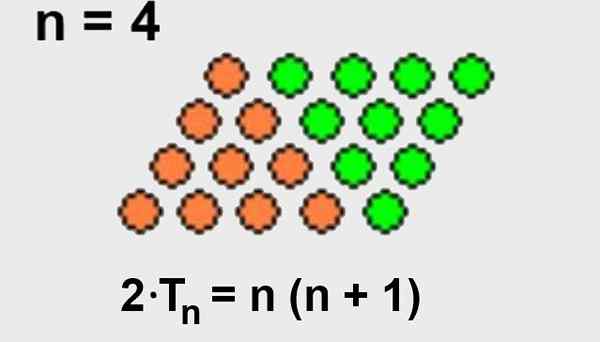Rysunek 2. Układ w kształcie kwadratu, w którym całkowita liczba punktów to liczba wierszy n pomnożona przez liczbę kolumn n+1. Całkowita liczba punktów jest również dwukrotnie większa niż w przypadku trójkątnego układu. Źródło: Wikimedia Commons.

- Demonstracja 2

Wykazać, że suma N-Ta trójkątna liczba z N-Mniej jeden Liczba trójkątna jest N kwadrat:

T_N + T_N-1= n²

Wykazano już, że liczba trójkątna N-Jest to podane przez:

T_N= ½ n (n+1)

Dlatego przednia liczba trójkątna to:

T_N-1 = ½ (n-1) ((n-1) + 1) = ½ n (n-1)

Suma obu pozostaje:

T_N + T_N-1 = ½ n (n + 1) + ½ n (n - 1)

½ n jest przyjmowane w celu uzyskania:

T_N + T_N-1 = ½ n [(n + 1) + (n - 1) = ½ n [n + 1 + n - 1]

I natychmiast wyrażenie jest uproszczone w wspornikach:

Może ci służyć: oszacowanie według interwałów

T_N + T_N-1 = ½ n [2 n] = ½ 2 n ⋅ n

Teraz, pamiętając, że ½ dla 2 to 1 i że n dla n jest n kwadratowe, masz:

T_N + T_N-1 = n²

Ta właściwość można również wykazać geometrycznie, trójkąt jest po prostu ukończony, tworząc kwadrat, jak pokazano na rycinie 3.

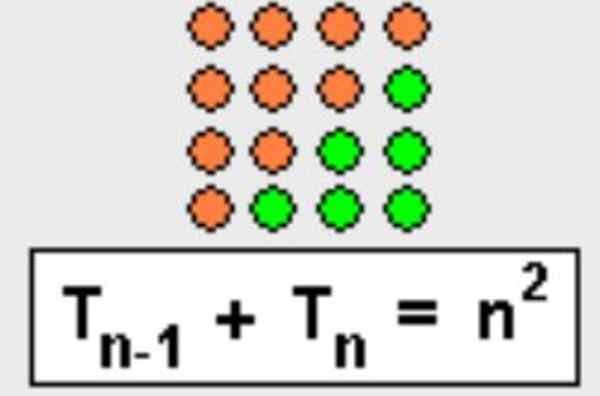Rysunek 3. Suma trójkątnej liczby N-ésimo z przednią liczbą trójkątną jest równa N Square. Źródło: Wikimedia Commons.

- Demonstracja 3

Różnica w trójkątnej liczbie zamówienia N minus trójkątna liczba zamówienia N-1 jest n:

T_N - T_N-1 = n

Można to przetestować po prostu, pamiętając, że następująca liczba trójkątna jest uzyskiwana z poprzedniej za pośrednictwem wzoru:

T_N = T_N-1 + N

I stamtąd jest to oczywiste T_N - T_N-1 = n. Łatwo jest go również wizualizować graficznie, jak pokazano na rycinie 4.

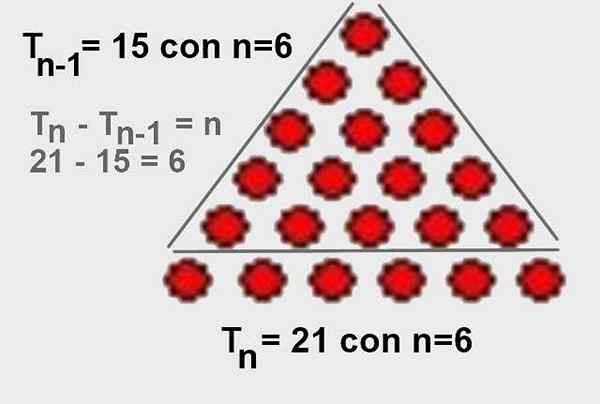Rysunek 4. Różnica trójkątnej liczby rzędu n mniejsza przednia trójkątna rzędu n-1 wynosi n. Źródło: Wikimedia Commons.

- Demonstracja 5

Suma pierwszych trójkątnych liczb nN Jest równy szóstej części produktu pomnożonego przez (n + 1) i pomnożony przez (n + 2):

S_N = ⅙ n (n + 1) (n + 2)

Użyjmy trójkątnej liczby zamówienia n: T_N= ½ n (n+1). Suma pierwszego N Trójkątne liczby oznaczają to dla S_N  

Na przykład, S₁ oznacza sumę pierwszego trójkątnego problemu, który niewątpliwie wyniesie 1.

Następnie zobaczmy, czy formuła, którą próbujemy wypróbować, jest zgodny z n = 1:

S₁ = ⅙ 1⋅2⋅3 = 1

Rzeczywiście, sprawdzany jest wzór dla n = 1. Łatwo jest sobie wyobrazić, że suma pierwszych trójkątnych liczb n+1 będzie sumą pierwszej n kolejnej liczby trójkątnej:

S_N+1 = S_N + T_N+1

Teraz przypuśćmy, że formuła S_N Jest to spełnione dla N, a następnie zastępujemy go w poprzednim wyrażeniu i dodajemy trójkątną liczbę zamówienia N+1:

S_N+1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]]]]

Może ci służyć: linia prostopadła: cechy, przykłady, ćwiczenia

Spójrzmy krok po kroku, co jest uzyskane:

-Wykonujemy sumę dwóch wyrażeń ułamkowych:

S_N+1 = [2 N (n + 1) (n + 2) + 6 (n + 1) (n + 2)] /12 

-Jest usuwany z licznika wspólnego do 2 (n + 1) (n + 2) i upraszcza:

S_N+1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6

Poprzedni wynik zgadza się z formułą SN Jeśli n+1 zostanie zastąpione, co zostało wykazane przez indukcję, wzór suma pierwszych terminów trójkątnych.

Numer czworościenny

Otrzymany wynik jest wywoływany Czworościenna liczba zamówienia n, Ponieważ to jest jak gromadzenie trójkątnych warstw, które tworzą czworościan, jak pokazano w następującej animacji.

Rysunek 5. Suma N trójkątnych liczb odpowiada stosowi warstw N, N-1, ..., 1 trójkątów, które tworzą regularne tetrahedron. Źródło: Wikimedia Commons.

Bibliografia

1. Camacho J. Nieoczekiwany wygląd liczb trójkątnych. Odzyskane z: Masscience.com
2. Claudio. Liczby trójkątne. Odzyskane z: po prostu liczby. Blogspot. com
3. Wikipedia. Liczba trójkątna. Odzyskane z: jest.Wikipedia.com
4. Wikipedia. Liczba trójkątna. Źródło: w:.Wikipedia.com
5. Wikipedia. Numer Tretrahedral. Źródło: w:.Wikipedia.com