Jakie są wyrażenia algebraiczne, które są najczęstsze?

 Wyrażenia algebraiczne Są to terminy matematyczne zawierające liczby i litery. W połączeniu z symbolami operacji matematycznych pozwalają na uzyskanie wzorów lub równań, z opisów wykonanych przez słowa. 

Z kolei te litery można dodawać, odejmować, mnożyć lub podzielić przez inne liczby, które mogą być wyraźne lub również reprezentowane przez litery.

Rysunek 1. Przykłady wyrażeń algebraicznych

[TOC]

Do czego są wyrażenia algebraiczne?

Na przykład wyrażenie:

2x + 3 

Jest to wyrażenie algebraiczne, w którym litera „x” reprezentuje liczbę być może nieznaną lub może przyjmować różne wartości.

Jaka jest zaleta użycia wyrażenia algebraicznego zamiast powiedzieć: „Dwa razy więcej dodana do 3”?

Po pierwsze, ekspresja algebraiczna zajmuje mniej miejsca. A następnie, jeśli x nie jest stałą liczbą, można podać różne wartości „x”, aby uzyskać różne wyniki tego wyrażenia.

Jest to znane jako wartość numeryczna ekspresji algebraicznej.

Na przykład, jeśli x = 1, wynik wynosi 2⋅1 + 3 = 2 + 3 = 5

Zamiast tego, wykonując x = -2, wyrażenie okazuje się być 2⋅ (-2) + 3 = -4 + 3 = -1

W innym rodzaju aplikacji wyrażenia algebraiczne reprezentują równanie lub równość, którą należy rozwiązać, aby poznać wartość liczby reprezentowaną przez listę.

Tutaj mamy proste równanie liniowe:

2⋅x + 3 = 7

Rozwiązaniem tego równania, które, nawiasem mówiąc, jest również wyrażeniem algebraicznym, jest:

x = 2

Ponieważ pomnożenie 2 przez 2 daje 4 plus 3 daje wynik: 7. Ale łatwiej jest zrozumieć, gdy wyrażenie algebraiczne jest używane zamiast opisywania wszystkiego za pomocą słów.

Najczęstsze wyrażenia algebraiczne

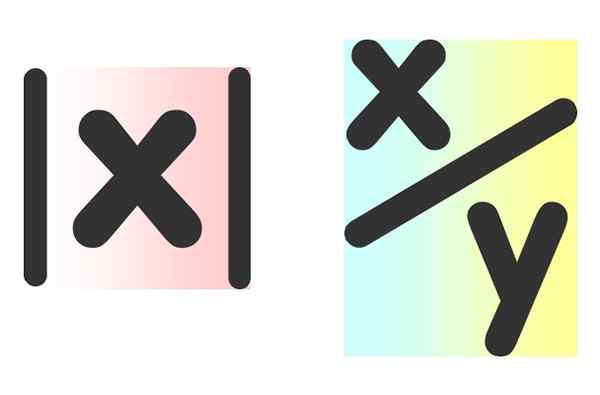Rysunek 2. Nieznane ilości często symbolizują z literami „X” i „Y”. Po lewej stronie jest wartość bezwzględna liczby i po prawej ilości w dwóch liczbach. Źródło: Pixabay.

Wyrażenia algebraiczne są szeroko stosowane w matematyce, nauce, gospodarce i administracji.

Poniżej znajduje się lista wyrażeń, które pojawiają się bardzo często w matematyce i innych tematach, w których wymagana jest propozycja.

Może ci służyć: obwód krąg: jak go wybrać i formuły, rozwiązane ćwiczenia

Zwykle nieznany lub nieznany numer jest oznaczony jako „x”, ale możemy użyć dowolnego innego listu alfabetowego zgodnie z uzgodnieniem.

Należy również pamiętać, że w wyrażeniu algebraicznym mogło to obejmować więcej niż jedną wartość, nieznaną lub zmienną, więc każdy z nich powinien otrzymać inną literę.

Lista wyrażeń algebraicznych

-Podwójny lub podwójny z liczby: 2x

-Suple z liczby więcej jednostek: 2m + 3

-Trzecia część liczby: z/3

-Dwa razy więcej niż trzecia część: 2x - x/3

-Kwadrat liczby: x²

-Kwadrat liczby więcej tej liczby: x² + 2x

-Duple z kwadratu liczby: 2x²

-Numer momentu obrotowego: 2n

-Liczba nieparzysty: 2n + 1

-Trzy kolejne liczby: x, (x+1), (x+2)

-Trzy kolejne liczby parzyste: 2n, 2n +2, 2n +4

-Trzy kolejne liczby nieparzyste, 2n + 1, 2n + 3, 2n + 5

-Określona liczba dodana do jego kolejnych: x +(x +1) = 2x +1

-Połowa kolejności całkowitej: (x+1)/2

-Potrójna połowa kwadratu liczby: 3. (1/2) x² = (3/2) x²

-Połowa jeszcze jednej liczby drugiej: x/2 + y/3

-Trzecia część produktu między kwadratem liczby a inną liczbą, do której odejmowano urządzenie: (1/3) x².(Y-1)

-Liczba i jest przeciwieństwo: a, -a

-Liczba i jego odwrotność: a, 1/a

-Suma liczby z kolejnymi podwyższonymi do kwadratu: x + (x + 1)²

-Odejmij 7 przy dwukrotności określonej liczby wysokości do kwadratu: (2x)² - 7

-Dwie liczby, które po mnożeniu dają 24: P.Q = 24

Może ci służyć: przemieszczenie kątowe

-Wartość bezwzględna liczby: │x│

-Iloraz między dwiema liczbami: x/y

-Pierwiastek kwadratowy iloczyn dwóch liczb: √x.I

Rysunek 3. To wyrażenie algebraiczne jest odczytywane jako „pierwiastek kwadratowy iloczyn dwóch liczb x i y”. Źródło: Pixabay.

-Jedna liczba, która przekracza kolejną w 30 jednostkach: x = y +30

-Dwa razy więcej niż jego połowa odejmowana: 2x- x/2

Problemy werbalne i ich wyrażenia algebraiczne

- Problem 1

Połowa krowy waży 100 kg więcej niż jedna czwarta tej samej krowy. Ile waży krowa?

Odpowiedź

Dla algebraicznej ekspresji tego problemu nazywamy X ciężarem krowy.

Połowa krowy waży ½ x. Czwarta część krowy waży ¼ x. Wreszcie wyrażenie algebraiczne odpowiadające: „Połowa krowy waży 100 kg ponad jedną czwartą” to:

½ x = ¼ x + 100

Aby wiedzieć, ile waży krowa, musisz zgrupować warunki z X po lewej stronie i pozostawić 100 po prawej:

(½ -¼) x = 100

¼x = 100

x = 400 kg

Krowa waży 400 kg.

- Problem 2

Na farmie liczba królików jest dwa razy więcej krów. Jeśli liczba krów wynosi 10. Ile jest królików?

Odpowiedź

Jeśli C jest liczbą królików, a V jest liczbą krów, to algebraiczna ekspresja stwierdzenia wynosi:

C = 2⋅V

V = 10

Zastąpienie wartości v w pierwszym z równań, które jest uzyskiwana:

C = 2 ⋅ 10 = 20

To znaczy farma ma dwudziestu królików.

- Problem 3

Jaka jest liczba pomnożona przez siedem i odejmij sześć?

Odpowiedź

Jeśli nazwiemy ten nieznany numer X, to wyrażenie algebraiczne można podniesienie:

Może ci służyć: właściwość asocjacyjna: suma, mnożenie, przykłady, ćwiczenia

7x - 6 = 29

Po 6 lewej stronie przechodzi na prawą stronę równości ze zmienionym znakiem:

7x = 29 + 6 = 35

Wynika z tego, że x = 35/7 = 5

- Problem 4

Dwa razy na określony numer 13 jest odejmowany, a 7 to 7. Jaki jest numer?

Odpowiedź

Jeśli nazwiemy ten numer X, jego równanie algebraiczne wynosi:

2 x - 13 = 7

Jaka jest wartość 2x ?

Odpowiedź jest taka, że ​​2x musi być (13 + 7), aby po usunięciu 13 było 7.

Oznacza to, że 2x musi być równy 20, to znaczy:

2x = 20

Liczba x, która pomnożona przez 2 da 20 to 10, dlatego:

x = 10

- Problem 5

Dwa kolejne liczby całkowite sumują 23. Zaproponuj równanie algebraiczne, które pozwala określić liczbę i znaleźć.

Odpowiedź

Załóżmy, że pierwsza z liczb to n, więc następującą jest n+1, a suma tych dwóch to n+(n+1). Wiadomo również, że suma suma wynosi 23, wówczas równanie jest napisane:

n + (n + 1) = 23

Rozwiązanie uzyskuje się najpierw upraszczając lewą stronę równości:

2 N + 1 = 23

Następnie 2 N jest wyczyszczone przez 1 do prawego członka ze zmienionym znakiem:

2 n = 23 - 1

Właściwy członek zostaje rozwiązany:

2 n = 22

Następnie n, przekazanie 2, które zwielokrotnia członka lewej, dzieląc członka prawej:

N = 22/2

I uzyskuje się końcowy wynik:

N = 11

Bibliografia

1. Baldor, a. Algebra. Cultural Cultural Cultural Culture C.DO.
2. Carena, m. 2019. Podręcznik matematyki przednicznicy. National University of the Coast.
3. Cimanet. Wyrażenia algebraiczne. Odzyskane z: Cinamet.UOC.Edu
4. Guzman p. Wyrażenia algebraiczne. Źródło: koncepcja finition.z
5. Kartkówka. Wyrażenia algebraiczne. Wyzdrowiał: może.UPRM.Edu
6. Martha. Przykłady wyrażeń algebraicznych. Odzyskane z: Superprof.Jest