Metoda tachtenberg, co jest, przykłady

On Metoda Trachtenberga Jest to system do wykonywania operacji arytmetycznych, głównie mnożenia, w łatwy i szybki sposób, gdy ich zasady będą znane i zdominowane.

Został opracowany przez rosyjskiego inżyniera Jakow Trachtenberga (1888–1953), kiedy był więźniem nazistów w obozie koncentracyjnym, jako forma rozproszenia w celu utrzymania zdrowia psychicznego, podczas gdy kontynuował w niewoli.

Rysunek 1. Tabliczka mnożenia. Źródło: Wikimedia Commons. Taulacat [CC BY-SA 3.0 (https: // creativeCommons.Org/licencje/by-sa/3.0)] [TOC]

Co to jest zalety i wady

Zaletą, którą reprezentuje ta metoda, jest to, że aby wykonywać mnożenie, nie jest konieczne.

Wadą jest to, że nie ma uniwersalnej reguły do ​​pomnożenia przez dowolną liczbę, ale reguła zmienia się w zależności od mnożnika. Jednak wzorce nie są trudne do zapamiętania i zasadniczo umożliwiają operacje bez papieru i ołówka.

W tym artykule skoncentrujemy się na zasadach, aby szybko się rozmnażać.

[TOC]

Przykłady

Aby zastosować metodę, konieczne jest znanie zasad, dlatego przedstawymy je jeden po drugim i z przykładami:

- Pomnóż liczbę przez 10 lub 11

Zasada mnożenia przez 10

-Aby pomnożyć dowolną liczbę przez 10, zero jest po prostu dodawane w prawo. Na przykład: 52 x 10 = 520.

Reguły do ​​pomnożenia przez 11

-Zero jest dodawane do początku i na końcu figury.

-Każda cyfra jest dodawana z prawym sąsiadem, a wynik jest umieszczony poniżej odpowiedniej cyfry oryginalnej figury.

-Jeśli wynik przekroczy dziewięć, wówczas odnotowano urządzenie i niewielki punkt jest pamiętany, że nosimy jednostkę, która zostanie dodana na sumę następnej liczby z prawym sąsiadem.

Szczegółowy przykład mnożenia przez 11

Pomnóż 673179 przez 11

Może ci służyć: Radio zbieżności: definicja, przykłady i ćwiczenia rozwiązane

06731790 x 11 =

--

= 7404969

Niezbędne kroki do osiągnięcia tego wyniku, zilustrowane przez kolory, są następujące:

-1 jednostki mnożnika (11) została pomnożona przez mnożnik 9 (06731790) i został dodany 0. Dycing jedności uzyskano: 9.

-Następnie mnoży 1 na 7 i dodaje dziewięć daje 16 i mamy 1, umieszczono tuzin cyfr: 6.

-Następnie dodaje się pomnożenie 1 przez 1 9 Za sto.

-Kolejna liczba jest uzyskiwana z pomnożenia 1 przez 3 plus sąsiadujące 1, wynika 4 Dla cyfry tysięcy.

-Jest mnożony 1 na 7, a sąsiad dodany wynikający z 10, zero umieszcza się (0) jako cyfra dziesięcin.

-Następnie 1 za 6 plus sąsiad 7 to 13 plus 1, który miał 14 lat, 4 jako cyfra stu tysięcy i zajmuje 1.

-Wreszcie pomnóż 1 przez zero, które zostało dodane na początku, dając zero więcej sąsiada 6 plus jeden, który wziął. Wreszcie 7 Dla cyfry odpowiadającej milionom.

- Mnożenie liczb od 12 do 19

Do pomnożenia przez 12 dowolnej liczby: 

-Zero jest dodawane do początku, a kolejne zero na końcu figury do pomnożenia.

-Każda cyfra jest podwojona z figury, która ma zostać pomnożona i dodaje z prawego sąsiada.

-Jeśli suma przekroczy 10 jednostki do następnej operacji duplikacji i dodaje z sąsiadem.

Przykład mnożenia przez 12

Pomnóż 63247 przez 12

0632470 x 12 =

-

758964

Szczegóły do ​​osiągnięcia tego wyniku, ściśle zgodne z określonymi zasadami, pokazano na poniższym rysunku:

Rysunek 2. Metoda Trachtenberg do pomnożenia dowolnej liczby przez 12. Źródło: f. Zapata.

- Rozszerzenie zasad mnożenia przez 13, ... do 19

Metodę mnożenia przez 12 można rozszerzyć na mnożenie przez 13, 14–19, po prostu zmieniając zasadę duplikacji w przypadku trzynastu, czternasto w przypadku 14 i tak dalej, aż do osiągnięcia 19.

Może ci służyć: macierz ortogonalna: właściwości, demonstracja, przykłady

Zasady dotyczące produktów do 6, 7 i 5

- Mnożenie przez 6

-Dodaj zera do początku i końca figury do pomnożenia przez 6.

-Dodaj połowę jego prawa po prawej do każdej cyfry, ale jeśli cyfra jest dziwna, aby dodać 5 dodatkowo.

Rysunek 3. Mnożenie rysunku przez 6, zgodnie z metodą Trachtenberga. Źródło: f. Zapata.

- Mnożenie przez 7

-Dodaj zera do początku i na końcu figury, aby się pomnożyć.

-Zduplikuj każdą cyfrę i dodaj dolną całą połowę sąsiada, ale jeśli cyfra jest dodatkowo, dodaj 5.

Przykład mnożenia przez 7

-Pomnóż 3412 przez 7

-Wynik to 23884. Aby zastosować zasady, najpierw zaleca się rozpoznanie dziwnych cyfr i umieszczenie małej 5, aby pamiętać o dodaniu tej liczby do wyniku.

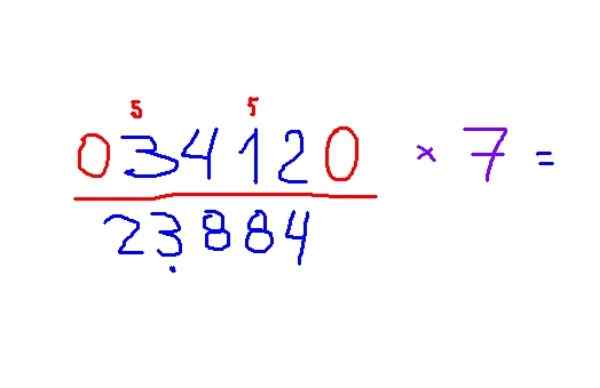Rysunek 4. Przykładowy mnożenie rysunku przez 7, zgodnie z metodą Trachtenberga. Źródło: f. Zapata.

- Mnożenie przez 5

-Dodaj zera do początku i na końcu figury, aby się pomnożyć.

-Umieść pod każdą cyfrą dolną połowę sąsiada po prawej stronie, ale jeśli cyfra jest dziwna, dodatkowo 5.

Przykład mnożenia przez 5

Pomnóż 256413 przez 5

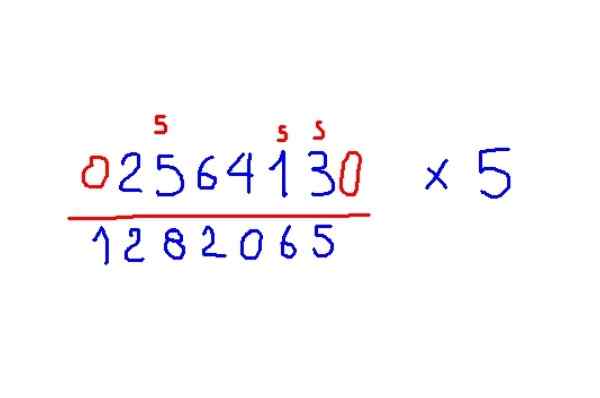Rysunek 5. Przykład mnożenia rysunku przez 5, zgodnie z metodą Trachtenberga. Źródło: f. Zapata.

Zasady produktów do 9

-Zero jest dodawane do początku, a drugiego na końcu figury, aby pomnożyć przez dziewięć.

-Pierwsza cyfra po prawej jest uzyskiwana od odejmowania odpowiedniej cyfry rysunku do pomnożenia.

-Następnie następna cyfra jest odejmowana i dodaje się sąsiad.

-Poprzedni krok jest powtarzany, aż osiągniesz zero mnożenia, gdzie odejmujemy 1 od sąsiada, a wynik jest kopiowany poniżej zera.

Może ci służyć: jakie są dzielniki 30? (Wyjaśnienie)

Przykład mnożenia przez 9

Pomnóż 8769 przez 9:

087690 x 9 =

--

78921

Operacje

10 - 9 = 1

(9-6) + 9 = 12 ( 2 I to wymaga 1)

(9-7)+1+6 =9

(9-8) +7 =8

(8-1) = 7

Mnożenie przez 8, 4, 3 i 2

-Dodaj zera do początku i na końcu figury, aby się pomnożyć.

-Dla pierwszej cyfry na prawym odejściu od 10, a wynik jest podwojony.

-Dla następujących cyfr odejmij od 9, wynik jest podwojony, a sąsiad dodaje się.

-Po osiągnięciu zerowego odejmij 2 od prawej po prawej stronie.

- Mnożenie przez 8

Przykład mnożenia przez 8

-Pomnóż 789 przez 8

Rysunek 6. Przykład mnożenia rysunku przez 8, zgodnie z metodą Trachtenberga. Źródło: f. Zapata.

- Mnożenie przez 4

-Dodaj zera po prawej i po lewej stronie mnożenia.

-Odejmij od 10 odpowiednią cyfrę urządzenia dodającego 5, jeśli jest to dziwna cyfra.

-Odejmij od 9 w postaci każdej cyfry mnożącej, dodając połowę sąsiada po prawej stronie i jeśli jest to dziwna cyfra, aby dodać 5 dodatkowo.

-Po osiągnięciu zera na początku mnożącego miejsce połowa sąsiada, z wyjątkiem jednego.

Przykład mnożenia przez 4

Pomnóż 365187 x 4

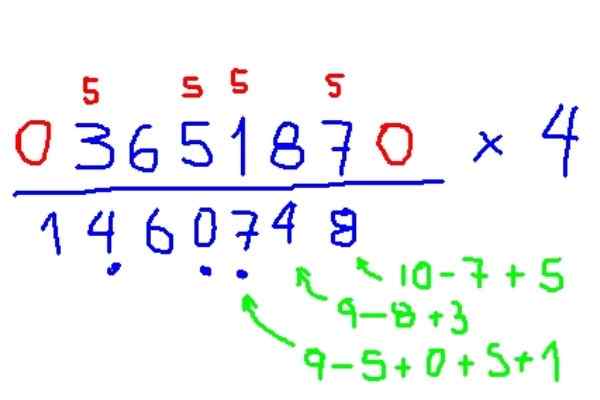Rysunek 7. Przykład mnożenia rysunku przez 4, zgodnie z metodą Trachtenberga. Źródło: f. Zapata.

- Mnożenie przez 3

-Dodaj zero do każdego końca mnożenia.

-Odejmij 10 z wyjątkiem cyfry urządzenia i dodaj 5, jeśli jest to dziwna cyfra.

-W przypadku innych cyfr odejmij 9 zduplikuj wynik, dodaj połowę sąsiada i dodaj 5, jeśli jest to dziwne.

-Po osiągnięciu zera nagłówka, umieść całą połowę sąsiada minus 2.

Przykład mnożenia przez 3

Pomnóż 2588 przez 3

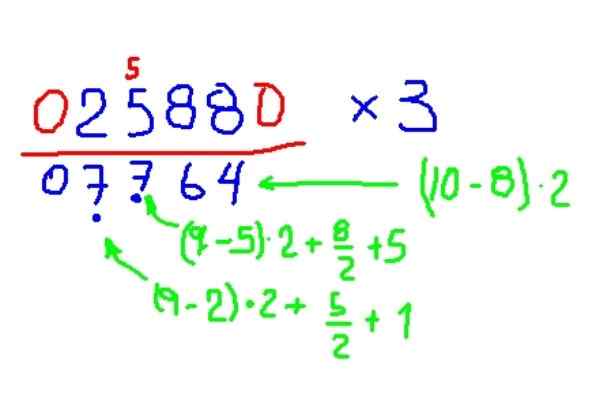Cyfra 8. Przykład mnożenia rysunku przez 3, zgodnie z metodą Trachtenberga. Źródło: f. Zapata.

- Mnożenie przez 2

-Dodaj zera do końców i podwajaj każdą cyfrę, jeśli przekroczysz 10, dodaj jeden do następnego.

Przykład mnożenia przez 2

Pomnóż 2374 przez 2

023740 x 2

04748

Pomnóż przez liczby złożone

Zastosowane powyżej reguły są stosowane, ale wyniki działają po lewej stronie liczba miejsc odpowiadających dziesiątkom, setkom i tak dalej. Spójrzmy na następujący przykład:

Ćwiczenia 

Pomnóż 37654 przez 498

0376540 x 498

301232 Zasada dla 8

338886 Zasada dla 9

150616 Zasada dla 4

18751692 Ostateczna suma

Bibliografia

1. Cutler, Ann. 1960.System prędkości Trachtenberg podstawowej matematyki. Doubleday & Co, NY.
2. Dialnet. Szybki podstawowy system matematyki. Odzyskane z: dialnet.com
3. Matematyczny narożnik. Szybkie mnożenie metodą Trachtenberga. Odzyskane z: rinconmatematycznego.com
4. System prędkości Trachtenberg podstawowej matematyki. Odzyskane z: Trachtenbergspeedmath.com
5. Wikipedia. Metoda Trachtenberga. Odzyskane z: Wikipedia.com