Historia tła i geometrii rozwoju z jego pochodzenia

Historia geometrii Zaczyna się od pierwszych cywilizacji, które w praktyce wykorzystywały tę gałąź matematyki, w szczególności ludy w dolinie Indo i Babilonie, które znały tępe trójkąty, około 3000.C.

W pismach egipskiego pisarza Ahmesa (1550 do.C.) Metody są stosowane do obliczenia obszaru koła. Ze swojej strony Babilończycy mieli ogólne zasady pomiaru wolumenu i obszarów. 

Ahme papirus lub rhind matematyczny

Obie cywilizacje, Egipcjanie i Babilończycy, znali wersje Twierdzenia Pitagorasa 1500 lat przed wersjami Pitagorean. Z drugiej strony Indianie z okresu wedyjskiego (1500-100 do.C.) Używana geometria w konstrukcji ołtarzy.

[TOC]

Starożytna Grecja

Grecy przez długi czas byli skłonni do rozwoju matematyki. Postacie takie jak Pitagoras i Platon, związane z liczbami ze wszystkim, co istnieje na świecie. Dla nich matematyka była kluczem do interpretacji wszechświata; Ten ideał nastąpił w obserwatorach Pitagoreańczyków przez kilka stuleci.

Tales of Miletus

Tales de Mileto był jednym z pierwszych Greków, którzy przyczynili się do postępów geometrii. Długi czas spędzony w Egipcie i z tych wyuczonej podstawowej wiedzy. Jako pierwszy ustalił wzory pomiaru geometrii.

Tales of Miletus

Udało mu się zmierzyć wysokość piramid Egiptu, mierząc jego cień w dokładnym momencie, w którym jego wysokość była równa miarowi jego cienia.

Pitagoras

Pitagoras

W ramach najbardziej znaczącego wkładu Pitagorasa (569 do.C. - 475 a.C.) Do geometrii jest słynne twierdzenie Pitagorasa, które ustala, że ​​w trójkącie prostokąta kwadrat przeciwprostokątnej (strona przeciwna kątowi prawego) jest równe sumie kwadratów pozostałych stron.

Elementy Euclida

Najważniejszą pracą, która została uratowana od czasów starożytnych, było badanie Elementy, z Euclid de Alejandría (325 A.C. - 265 a.C.), wykonane w latach 300.C. Jest to dzieło o wielkiej wartości historycznej, które służyło jako podstawa nauczania matematyki od ponad 2000 lat.

Euclid

Elementy To była jedna z pierwszych książek i kompilacji badań, które wyjaśniły zasady matematyczne, które można zastosować w każdej sytuacji. Obejmuje postulaty, które są podstawowymi zasadami geometrii w ich pracy. Z drugiej strony istnieją zasady ilościowe znane jako podstawowe pojęcia.

Nauczanie euclidów zmniejszyło instrumenty budowlane w obrębie geometrii tylko do dwóch: zasada bez środków i kompas. Wygenerowało to trzy klasyczne problemy, które nie znalazły odpowiedzi do dziewiętnastego wieku: kwadratryka koła, powielanie kostki i trisekcja kąta. 

Może ci służyć: w którym stuleciu Hiszpanie podbili Tenochtitlán?

W przypadku starożytnych dwoma idealnymi jednostkami geometrycznymi były linia prosta i okrąg, więc większość proponowanych twierdzeń geometrycznych była produktem eksploracji z tymi instrumentami.

Geometria w astronomii

Geometria również korzystała dla Greków pod względem badania gwiazd. Obliczyli ruchy przez obserwację i stworzyli geometryczne płaszczyzny nieba, ustanawiając Ziemię jako punkt centralny, a zarówno słońce, jak i księżyc oraz inne planety i istoty, które się wokół nich poruszały, obracając się w zestawie kręgów. 

Jednym z najbardziej wpływowych wkładów było Almagest, Napisane w drugim wieku D.C Claudio Ptolemeusza (100 d. C.- 170 d.C), astronomiczny pojemnik traktatowy katalogu gwiazd. Był to najbardziej kompletny tekst jego czasów i wpłynął na badania astronomiczne w sposób transcendentalny, dopóki średni wiek jest bardzo zaawansowany. Był to część mediów, która najbardziej spopularyzowała system geocentryczny, który twierdzi, że Ziemia była centrum wszechświata.

Ptolemeusz

Wpływ islamski

W IX stuleci, kiedy świat arabski był w wielkiej ekspansji, znaczna część jego kultury przeniknęła kilka dziedzin nauki i sztuki. Byli wielkimi fanami dzieł matematycznych i filozoficznych Greków. 

Jednym z najczęściej badanych gałęzi w ich potrzebach była astronomia, aby zlokalizować dokładną orientację, w której MECA miała wykonać zdania.

Po badaniach Euclida i innych wkładów, takich jak badania Ptolemeusza, muzułmanie rozwinęli rzut stereograficzny, to znaczy projekcja kuli niebieskiej w płaszczyźnie, aby użyć go jako mapy. Oznaczało to postęp w badaniu trygonometrii.

Wśród najbardziej reprezentatywnych postaci jest Thābit Ibn Qurra (826/36-901), którzy dokonali odpowiednich tłumaczeń starożytnych tekstów Apolloniusa, Archimedes, Euclid i Ptolemeusza. Niektóre z nich są jedynymi ocalałymi wersjami starożytnych pism.

Eksploracje dotyczące geometrii astronomicznej pozwoliły również na stworzenie jednego z najbardziej reprezentatywnych instrumentów, astrolabio, które uprościły obliczenia astronomiczne momentu. Ponadto ten instrument pozwolił im również poznać czas i wreszcie zdobyć wskazówki do MECA. 

Może ci służyć: 8 zwyczajów i tradycji mixtecs

Rozwój dziedzictwa europejskiego

W XII wieku, po wstawieniu klasycznych nauk Greków dzięki ekspansji muzułmańskiej i rozwoju tych samych odkryć, tłumaczenia tekstów łaciński. 

To zrobiłoby miejsce dla nowej nauki w Europie, która byłaby promowana przez renesans. Ponowne odkrycie pojęć, takich jak „dowody”, rozpoczęła się koncepcja wśród Greków, która była zainteresowana demonstracją postulatów w rzeczywistości.

Geometria w sztuce

Wiedza znalazła również odzwierciedlenie w sztuce, takiej jak malarstwo lub architektura, ponieważ geometria zaczęłaby być podstawową częścią rozwoju perspektywy w sztuce.

Filippo Brunelleschi (1377-1446), był tym, który udało się rozwinąć perspektywę liniową poprzez matematykę. Celem tej teorii było przedstawienie w płaszczyźnie trzywymiarowej przestrzeni od tego, jak była postrzegana przez ludzkie oko. Zatem stwierdza, że ​​wszystkie linie na zdjęciu musiały zbiegać się lub znaleźć wyciek w celu wygenerowania odczucia głębokości. 

Filippo Brunelleschi. Źródło: I, Sailko/CC BY-S (http: // CreativeCommons.Org/licencje/by-sa/3.0/)

Brunelleschi jako pierwszy opisał perspektywę jako procedurę naukową, która działała jako podstawa kolejnych miejsc pracy w sztuce.

W innych przykładach zastosowania geometrii do studiowania sztuki i istoty ludzkiej w sobie jest dziełem Leonarda da Vinci (1452-1519) na jego rysunku Mężczyzna Vitruvio. Jest to badanie oparte na najdoskonalszych proporcjach dla ludzkiego ciała poprzez analizę geometryczną jego struktury.

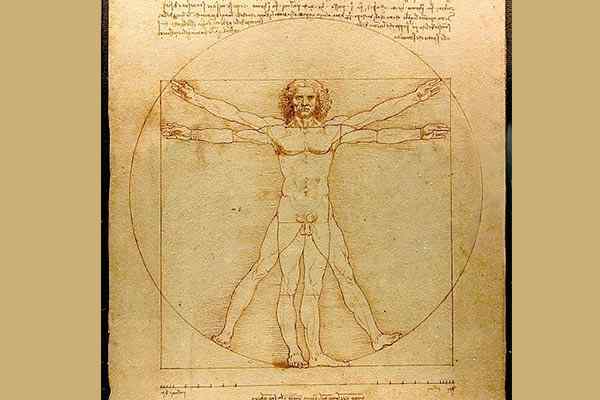The Man of Showcase autorstwa Leonardo da Vinci / Public Domena

Wśród innych obszarów wyróżnia się również architektura, w której różne elementy, takie jak symetria i równowaga, zaczęły pojawiać się jako podstawowe cechy. Kwadratowe, prostokątne drzwi i okna, ustawione w zrównoważony sposób; Zastosowanie klasycznych elementów starożytności, takich jak kolumny, kopuły i sklepienia.

Krok do nowoczesności

Analiza perspektyw i prognoz podczas renesansu była jedną z zachęt do wzbudzenia zainteresowania matematyków. Od tego momentu zaczynają być bardziej solidne i złożone podstawy matematyczne.

Jednym z najważniejszych dzieł dla nowoczesności była rozbrajona architekta Girarda (1591-1661), która przypuszczała początek geometrii rzutowej. Z jednej strony ustalił, że równoległe linie w projekcji powinny zbiegać się w punkcie na linii nieskończoności, to znaczy horyzont.

Może ci służyć: rebelia tuxtepec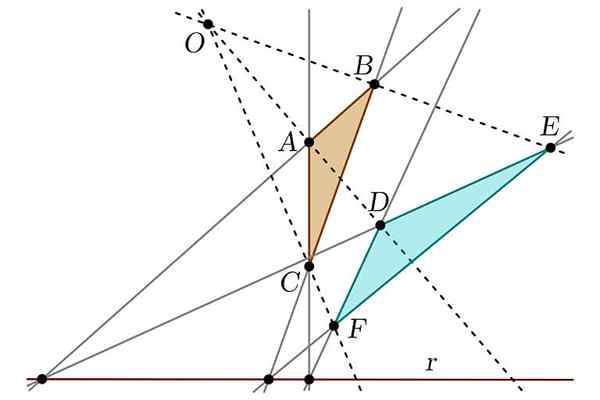Twierdzenie Disnark

Z drugiej strony odkrył również, co zostanie uznane za twierdzenie o nieusie, które ustanawia związek między dwoma liczbami, które można uznać za „rzutowe”. Był również odpowiedzialny za uproszczenie prac Apolloniusa w odniesieniu do sekcji stożka, tworząc analogie między tą figurą a cylindrem.

Kolejnym wielkim wydarzeniem tego okresu było stworzenie geometrii analitycznej poprzez badania René Descartes (1596-1650) i Pierre de Fermat (1601-1665) niezależnie. To jest badanie geometrii za pomocą układu współrzędnych. 

René Descartes pracujący na pulpicie. Wikimedia Commons

Geometria nieeuklidyjska

W XVIII i XIX wieku badania rozpoczęły się w geometrii nieeuklidowskiej. W szczególności byli Gauss, Johann Bolei i Lobachevsky, którzy stwierdzili, że nie można zweryfikować piątego postulatu Euclida, znanego jako równoległy postulat.

W ten sposób opracowali rodzaj geometrii, w której ten postulat został zakwalifikowany jako fałszywy. Ta nowa forma była skuteczna, dając satysfakcjonujące wyniki w stylach geometrii, które niekoniecznie spełniały wszystkie postulaty Euclida. Zatem geometria hiperboliczna i geometria eliptyczna urodziła się później.

Warto podkreślić pracę Leonharda Eulera (1707-1783) w XVIII wieku, w odniesieniu do rozwoju notacji matematycznej. Następnie XX wieku przyniósłby ze sobą rozwój bardziej specyficznych dziedzin geometrii, w tym:

-Geometria algebraiczna: Jest to gałąź matematyki, która łączy abstrakcyjną algebrę i geometrię analityczną.

-Geometria skończona: Jest to system geometryczny składający się z skończonej ilości punktów, to znaczy mają one koniec lub limit, a zatem można je zmierzyć.

-Geometria cyfrowa: Jest to gałąź informatyki, że badanie algorytmów i struktur danych, które mogą być reprezentowane w kategoriach geometrycznych. 

Bibliografia

1. (2016) Co uczyniło elementy Euclid jedyną książką, która może konkurować z Biblią. BBC. BBC odzyskało.com
2. Trzy klasyczne problemy greckiej matematyki. University of Antioquia. Wyzdrowiał z nauczania.Ty.Edu.współ
3. Heilbron J.L (2020). Geometria. Encyclopædia Britannica. Odzyskane z Britannica.com
4. Historia geometrii. Wikipedia, wolna encyklopedia. Odzyskane z.Wikipedia.org
5. Geometria analityczna. Wikipedia, wolna encyklopedia. Odzyskane z.Wikipedia.org
6. (2017) Geometria i matematyka w renesansie. Odzyskane z ukessaysów.com
7. Sáiz a. Perspektywa liniowa w Brunelleschi. University of Valencia. UV odzyskało.Jest
8. Redaktorzy Encyclopaedia Britannica (2019). Architektura renesansu. Encyclopædia Britannica. Odzyskane z Britannica.com
9. Andersen K (2020). Girard rozbrojenie. Encyclopædia Britannica. Odzyskane z Britannica.com
10. (2011) Interesujące wprowadzenie do geometrii obliczeniowej. Pobrano z Gaussian.com