Tożsamości trygonometryczne (przykłady i ćwiczenia)

tożsamość trygonometryczna Są to relacje między przyczynami trygonometrycznymi, które są prawdziwe dla każdej wartości zmiennej. Na przykład:

Tan θ = sin θ /cos θ

Jest to tożsamość trygonometryczna, która dotyczy trzech przyczyn kąta θ, stycznej, piersi i cosinus.

Rysunek 1. Niektóre tożsamości trygonometryczne szeroko stosowane w obliczeniach. Źródło: f. Zapata.

Ta tożsamość jest prawdziwa dla całej wartości, z wyjątkiem tych, które czynią 0 mianownik. Cos θ wynosi 0 dla θ = ± π/2, ± 3π/2, ± 5π/2… Innym przykładem tożsamości trygonometrycznej jest:

sin x . Sec x . CTG x = 1

[TOC]

Demonstracja

Istnieją dwa podstawowe sposoby wykazania, że ​​tożsamość trygonometryczna jest prawdziwa:

1- Przekształcanie jednego z członków równości w drugiego, poprzez wygodne manipulacje algebraiczne.

2- Rozwijaj obu członków równości osobno, aż odpowiednie ostateczne wyrażenia każdego z nich są dokładnie takie same.

W proponowanej tożsamości zamierzamy przekształcić lewą stronę równości, dla której wyrażamy CTG X i Sec X pod względem piersi i cosinusa w następujący sposób:

CTG x = cos x / sen x

Sec x = 1 /cos x

Zastępujemy to wyrażenie po lewej stronie tożsamości i upraszczamy:

sin x . (1/cos x). (cos x / sen x) = (sin x. cos x / cos x . sin x) = 1

A prawdziwość tożsamości jest już udowodniona.

Rodzaje tożsamości trygonometrycznej

Istnieje kilka rodzajów tożsamości trygonometrycznej. Następnie krótko opiszemy główne:

- Podstawowe tożsamości trygonometryczne

Rozróżniamy dwa rodzaje podstawowych tożsamości:

I) te, które są wyrażone z podstawowych powodów, cosinus i styczna:

• Sec x = 1 /cos x
• Szkoda x / 1 / sin x
• CTG x = 1 / tg x
• Tg x = sin x /cos x
• CTG x = cos x / sen x

I) te pochodzące z parytetu. Wiemy za pośrednictwem wykresu, że Sen X jest dziwną funkcją, co oznacza, że:

Może ci służyć: 60 dzielników

sin (-x) = - sin x

Ze względu na swoją część COS X jest zatem parą:

cos (-x) = cos x

Więc:

tg (-x) = sen (-x) / cos (-x) = -sen x / cos x

Podobnie:

• COTG (-x) = -ctg x
• sec (-x) = sec x
• HARM (-x) = - Harm x

- Tożsamość pitagorejska

Są to te uzyskane z zastosowania twierdzenia Pitagorasa do prostokąta trójkąta kotów A i B i Hindenusa C. Zobaczmy:

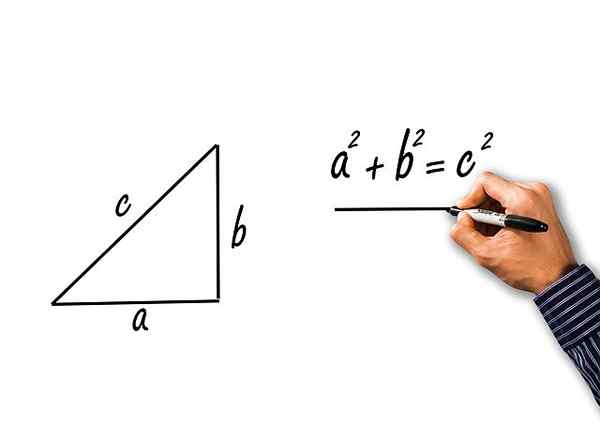Rysunek 2.- Z twierdzenia Pitagorasa uzyskano trzy pitagorejskie tożsamości trygonometryczne. Źródło: Pixabay.

Twierdzenie Pitagorasa stwierdza, że:

C² = a² + B²

Dzielenie wszystkiego między C²:

C² / C² = (a² / C²) + (B² / C²)

Termin po lewej jest 1 i pamięta, że ​​zatokę i cosinus ostrego kąta α są zdefiniowane jako:

sin α = a/c

cos α = b/c

Wynik:

1 = (sin α)² + (cos α)²

Ta tożsamość jest znana jako podstawowa tożsamość.

Procedurę można przeprowadzić, dzieląc się między² oraz b², który daje powstanie dwóch kolejnych tożsamości:

Sec² α = 1 + TG² α

Har² α = 1 + CTG² α

- Wzory dla cosinusu i piersi suma/odejmowanie kątów

Główne tożsamości trygonometryczne dla cosinus, piersi i stycznej suma i odejmowania są następujące:

Demonstracja SEN (α + β) i COS (α + β)

Tożsamości te można wykazać geometrycznie lub również poprzez wzór Eulera:

I^iα = cos α + i sin α

Spójrzmy na to, co dzieje się z formułem podczas wymiany suma dwóch kąta α i β:

I^{I (α +β)} = cos (α + β) + i sin (α + β)

Ta ekspresja jest złożona, jego prawdziwą częścią jest cos (α + β), a jego wyobrażoną częścią jest I sin (α + β). Utrzymujemy ten wynik, aby użyć go później i skupiamy się na opracowaniu części wykładniczej:

I^{I (α +β)} = e^iα ⋅ e^Iβ = (cos α + i sin α) . (cos β + i sin β) =

Może ci służyć: heksagonalny pryzmat

= cos α⋅COS β + cos αrzęg β + i⋅sen α cos β - Sen α⋅Sen β

Prawdziwą częścią tego wyrażenia jest ta, która nie jest mnożona przez jednostkę wyobrażoną „I”:

COS α⋅COS β - SEN α. Sen β

Część wyimaginowana jest zatem:

I (cos α⋅Sen β + Sen α⋅Cos β)

Aby dwa złożone wyrażenia były takie same, prawdziwa część jednego musi być równa prawdziwej części drugiej. To samo dotyczy wyimaginowanych części.

Wyjmujemy zapisany wynik i porównujemy go do tego:

cos α. cos β - Sen α. sin β = cos (α + β)

I (cos α⋅sen β + Sen α⋅Cos β) = i sin (α + β)

sin (α + β) = (cos α. Sin β + Sen α⋅Cos β)

- Wzory dla podwójnego kąta

W poprzednich wzorach przyjmujemy β = α i rozwijamy:

sin (α + α) = Sen 2 α = Sen α⋅Cos α + cos α. sin α = 2⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α⋅cos α - Sen α⋅Sen α = cos² α - Sen ² α

TG (α + α) = tg 2 α = [tg α + tg α] / [1- tg α⋅tg α] = 2Tg α / 1- tg² α

Jeśli w drugim wyrażeniu COS zostanie zastąpiony² α = 1 - Sen² α otrzymuje:

cos 2 α = cos² α- (1- cos² α) = 2 cos² α -1

- Formuły pół kąta

W tym ostatnim wyrażeniu zastępujemy α α/2, pozostaje następujące:

cos α = 2 cos ²(α/2) -1

Clearing:

Rozwiązane ćwiczenia

- Ćwiczenie 1

Pokazują, że:

Rozwiązanie

Zamierzamy pracować algebraicznie termin lewy, aby wyglądał jak w porządku. Jak pojawia się w odpowiednim okresie, pierwszym krokiem jest wyrażenie cos²X Pod względem Sen X, aby wszystko było pod względem tego samego powodu trygonometrycznego:

Może ci służyć: ułamek równoważny 3/5 (rozwiązanie i wyjaśnienie)

Następnie 1 - Sen jest czynnikiem² x za różnicę idealnych kwadratów. Aby to zrobić, wynika z podstawowej tożsamości:

sałata²X = 1 - Sen² X

1 - Sen² x = (1- sin x) (1+Senx)

A czynnik faktoryzacja w pierwotnym wyrażeniu jest zastąpiona:

Termin (1- Senx) jest uproszczony i pozostaje równość:

1 + Sen X = 1 + Senx

- Ćwiczenie 2

Rozwiąż następujące równanie trygonometryczne i podaj rozwiązanie dla wartości od 0 do 360º:

Tg x + sec² x = 3

Rozwiązanie

W okresie lewej istnieją dwa powody trygonometryczne, dlatego musisz zredukować wszystko do jednego, aby móc wyczyścić nieznane. Termin Sec² X jest wyrażane przez jedną z tożsamości Pitagoreańskiej:

Sec² α = 1 + TG² α

Zastępując równanie:

TG X + 1 + TG² x = 3

Zatrzymanie warunków:

TG² x + tg x + 1 = 3

To równanie jest rozwiązywane poprzez zmianę zmiennej:

tg x = u

Lub² + U + 1 - 3 = 0 → U² + U - 2 = 0

To równanie drugiego stopnia jest łatwo rozwiązywane przez czynniki:

(U +2) (u-1) = 0

Dlatego u₁ = -2 i u₂ = 1, równoważny:

TG x₁ = -2

TG x₂ = 1

Wreszcie:

X₁ = arctg (-2) = 296.6th

X₂  = Arctg (1) = 45º

Bibliografia

1. Carena, m. 2019. Podręcznik matematyki przednicznicy. National University of the Coast.
2. Figuera, J. 1999. Matematyka. 1st. Urozmaicony. Bolivarian Collegiate Editions.
3. Hoffman, J. Wybór problemów z matematyką. Tom 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Tożsamości i formuły trygonometrii. Odzyskane z: jest.Wikipedia.org.
6. Zapata, f. 4 sposoby rozwiązania równania drugiego stopnia. Odzyskane z: Francessphysics.Blogspot.com.
7. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.