Jednostkowe funkcje i aplikacje trygonometryczne koła

On Jednolity krąg Jest to okrąg promienia równy 1, który zwykle koncentruje się na punkcie (0,0) układu współrzędnych kartezjańskich Xy. Służy do łatwego zdefiniowania przyczyn trygonometrycznych kątów przez prostokąty.

Równanie jednolitego okręgu koncentrujące się na pochodzeniu to:

X² + I² = 1

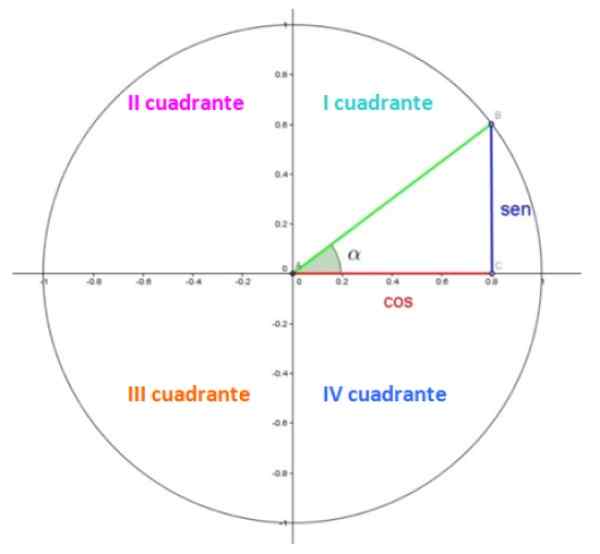
Rysunek 1. Okrąg jednostki. Źródło: Wikimedia Commons.

Na rycinie 1 mamy koło jednostkowe, w którym każdy pokój znajduje się w ćwiartce. Kwadranty są ponumerowane z liczbami rzymskimi i są liczone antyhoraryczne.

W pierwszej ćwiartce znajduje się trójkąt. Kategorie, odpowiednio na czerwono i w niebiesko 0.8 i 0.6, podczas gdy przeciwprostokątna w zielonych mierzy 1, ponieważ jest to radio.

Ostry kąt α jest kątem centralnym w pozycji standardowej, co oznacza, że ​​jego wierzchołek pokrywa się z punktem (0,0) i początkową stroną z dodatnią osą x. Kąt jest mierzony wbrew dłoni zegara, a konwencją przypisano mu znak dodatni.

Cóż, w okręgu jednostkowym współrzędne Coseno i sinus α są odpowiednio współrzędnymi x i y punktu b, które w pokazanym przykładzie wynoszą 0.8 i 0.6.

Z tych dwóch są zdefiniowane:

• TG α = sin α/cos α = 0.6/0.8 = 0.75
• Sec α = 1/ cos α = 1/0.8 = 1.25
• szkoda α = 1 / sin α = 1/0.6 = 1.66 ..
• CTG α = 1/tg = 0.8/0.6 = 1.33 ..

[TOC]

Jednolitowe zastosowania w kółkach

Jeśli ograniczymy się do prostokątów, przyczyny trygonometryczne będą stosowane tylko do ostrych kątów. Jednak przy pomocy koła jednostkowego obliczenia przyczyn trygonometrycznych jest rozszerzone na dowolny kąt α.

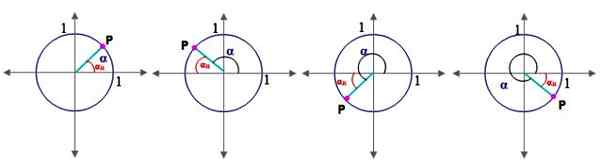Rysunek 2.- Kąty w ćwiartkach i kąt odniesienia w okręgu jednostkowym. Źródło: f. Zapata.

W tym celu należy najpierw zdefiniować pojęcie kąta odniesienia α_R:

Może ci służyć: Zestaw skończony: właściwości, przykłady, rozwiązane ćwiczenia

Kąt odniesienia

Niech α będzie kątem w pozycji standardowej (ten, którego ten Początkowa strona pokrywa się z dodatnią osą x), jego kąt odniesienia α_R Jest jednym z nich strona końcowa i oś x. Ryc. 2 pokazuje kąt odniesienia dla kąty w I, II, III i IV kwadrantu.

Dla każdego kwadrantu kąt odniesienia jest obliczany w następujący sposób:

-Pierwszy kwadrant: α_R = α

-Drugi kwadrant: α_R = 180º - α

-Trzeci kwadrant: α_R = α - 180º

-Czwarty kwadrant: α_R = 360º - α

Zauważ, że pierwszy kąt kwadrantu α pokrywa się z kątem odniesienia. Cóż, trygonometryczne przyczyny kąta α są takie same jak kąt odniesienia, z znakami według tych, którzy mają kwadranty, w których końcowa strona α spadnie.

Innymi słowy, przyczyny trygonometryczne Coseno i pierś kąta α pokrywają się ze współrzędnymi punktów P, zgodnie z ryc. 2.

Na poniższym rysunku widzimy trygonometryczne przyczyny niektórych godnych uwagi kątów, wyceniane z koła jednostkowego.

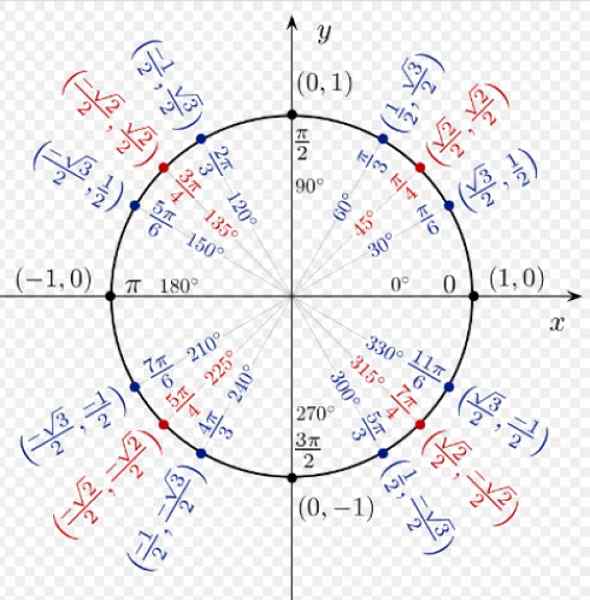Rysunek 3. Współrzędne niektórych znaczących punktów w okręgu jednostkowym. Źródło: Wikimedia Commons.

Powody, dla których Coseno i piersi dowolnego kąta w ćwiartce I są dodatnie. Dla α = 60º mamy współrzędne (1/2; √3/2), które odpowiadają odpowiednio cos 60º i Sen 60º.

Współrzędne α = 120º to (-1/2; √3/2), ponieważ w drugiej ćwiartce współrzędne x jest ujemne.

Układ wykresów cosinus i zatok

Z pomocą koła jednostkowego i współrzędnych punktów p, możliwe jest narysowanie wykresów funkcji cos t i sen t, jak zobaczymy poniżej.

Może ci służyć: przemieszczenie kątowe

W tym celu kilka pozycji punktu P (t) znajduje się w okręgu jednostkowym. Zaczniemy od wykresu funkcji f (t) = Sen t.

Możemy zauważyć, że kiedy przejdziemy od t = 0 do t = π/2 (90º), wartość Sen t wzrasta do 1, co jest wartością maksymalną.

Z drugiej strony, od t = π/2 do t = 3π/2 wartość sin t spada z 1, przechodząc przez 0 przy t = π do minimum -1 przy t = 3π/2.

Rysunek pokazuje wykres pierwszego cyklu f (t) = Sen t, który odpowiada pierwszego powrotu do okręgu jednostkowego, funkcja ta jest okresem okresowym 2π.

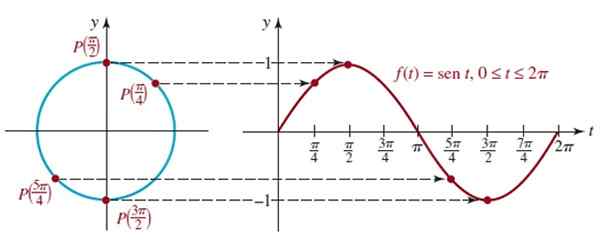Rysunek 4. Rysunek wykresu f (t) = sen t dla cyklu. Źródło: Zill, D. Algebra, trygonometria i geometria analityczna.

Można przeprowadzić analogiczną procedurę w celu uzyskania wykresu funkcji f (t) = cos t, jak pokazano w następującej animacji:

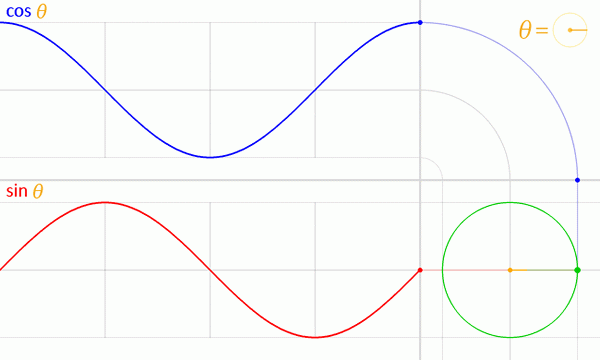Rysunek 5. Wykresy funkcji sinus i cosinus z koła jednostkowego. Źródło: Wikimedia Commons.

Seno i Coseno funkcjonują właściwości

-Obie funkcje są ciągłe w zbiorze liczb rzeczywistych, a także okresowych, z okresu 2π.

-Domena funkcji f (t) = Sen t i f (t) = cos t są liczbami rzeczywistymi: (-∞, ∞).

-W przypadku drogi piersi lub zatoki i cosinus masz przedział [-1,1]. Wsporniki wskazują, że -1 i 1 są dołączone.

- Sin t zera są wartościami odpowiadającymi Nπ z N całkowitą, podczas gdy zera cos t to [(2n+1)/2], a n również całości.

-Funkcja f (t) = sin t jest dziwna, ma symetrię w odniesieniu do pochodzenia, gdy funkcja cos t jest równa, jej symetria dotyczy osi pionowej.

Może ci służyć: losowe wybory z lub bez zamiennika

Rozwiązane ćwiczenia

- Ćwiczenie 1

Biorąc pod uwagę cos t = - 2/5, która jest poziomą współrzędną punktu P (t) w okręgu jednostkowym w drugim kwadrancie, uzyskaj odpowiednią pionową współrzędną Sen t.

Rozwiązanie

Ponieważ p (t) należy do koła jednostkowego, w którym jest spełnione, że:

X² + I² = 1

Dlatego:

y = ± √ 1 - x²

Ponieważ p (t) jest w drugim kwadrancie, zostanie pobrana wartość dodatnia. Pionowa współrzędna punktu P (t) wynosi y:

y = √ 1 - (-2/5)² = √0.84

- Ćwiczenie 2

Model matematyczny dla temperatury T W stopniach fahrenheita każdego dnia, T Kilka godzin po północy jest podawany przez:

T (t) = 50 + 10 Sen [(π /12) × (t - 8)]

Z TYM rozumianym od 0 do 24 godzin. Znajdować:

a) Temperatura o 8 rano.

b) godziny, podczas których t (t) = 60 °f

c) maksymalne i minimalne temperatury.

Rozwiązanie

Wymieniamy t = 8 w danej funkcji:

T (8) = 50 + 10 Sen [(π/12) × (T-8)] = 50 + 10 Sen [(π/12) × (8-8)] =

= 50 + 10 x Sen 0 = 50 ºF

Rozwiązanie b

50 + 10 Sen [(π/12) × (T-8)] = 60

Jest to równanie trygonometryczne i musisz wyczyścić nieznane „t”:

10 Sen [(π/12) × (t -8)] = 60 - 50 = 10

sin [(π/12) × (t-8)] = 1

Wiemy, że Sen π/2 = 1, dlatego argument piersi musi wynosić 1:

(π/12) × (T-8) = π/2

T-8 = 6

t = 14 h

Stwierdzono, że 14 godzin po północy temperatura wynosi 60 °, to znaczy 14.00. Nie ma innej godziny przez cały dzień (24 godziny), w której tak się dzieje.

Rozwiązanie c

Maksymalna temperatura odpowiada wartości, w której Sen [(π/12) × (T-8)] = 1 i wynosi 60 ° F. Z drugiej strony minimum występuje, jeśli Sen [(π/12) × (t -8)] = -1 i wynosi 40 ºF.

Bibliografia

1. Figuera, J. 1999. Matematyka. 1st. Urozmaicony. Bolivarian Collegiate Editions.
2. Hoffman, J. Wybór problemów z matematyką. Tom 4.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Matematyka jest zabawna. Koło jednostkowe. Odzyskane z: z: MathSisfun.com.
5. Wikipedia. Tożsamości i formuły trygonometrii. Odzyskane z: jest.Wikipedia.org.
6. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.