Losowa koncepcja eksperymentu, przestrzeń próbki, przykłady

Mówi się o Losowy eksperyment Gdy wynik każdej konkretnej próby jest nieprzewidywalny, nawet jeśli można ustalić prawdopodobieństwo wystąpienia określonego wyniku.

Należy jednak wyjaśnić, że nie można odtworzyć tego samego wyniku losowego systemu o tych samych początkowych parametrach i warunkach w każdym badaniu eksperymentu.

Rysunek 1. Dyspozycja Dice to przypadkowy eksperyment. Źródło: Pixabay.

Dobrym przykładem losowego eksperymentu jest wprowadzenie kości. Nawet gdy zadbasz o uruchomienie kości w ten sam sposób, przy każdej próbie zostanie uzyskany nieprzewidywalny wynik. W rzeczywistości jedyną rzeczą, którą można potwierdzić, jest to, że rezultatem może być niektóre z następujących: 1, 2, 3, 4, 5 lub 6.

Uruchomienie waluty jest kolejnym przykładem losowego eksperymentu z tylko dwoma możliwymi wynikami: twarz lub pieczęć. Chociaż waluta jest uruchamiana z tej samej wysokości i w ten sam sposób, czynnik przypadkowy będzie zawsze obecny, co powoduje niepewność każdej nowej próby.

Przeciwieństwem losowego eksperymentu jest eksperyment deterministyczny. Na przykład wiadomo, że za każdym razem, gdy woda jest gotowana na poziomie morza, temperatura wrzenia wynosi 100 ° C. Ale nigdy się nie zdarza, że ​​utrzymując te same warunki, wynikiem jest czasami 90 ° C, kolejne 12 0ºC, a czasem 100 ° C.

[TOC]

Przykładowa przestrzeń

Zestaw wszystkich możliwych wyników losowego eksperymentu nazywany jest Przykładowa przestrzeń. W przypadkowym eksperymencie uruchomienia kości próbki jest:

D = 1, 2, 3, 4, 5, 6.

Ze względu na to, na uruchomieniu waluty przestrzeń próbki to:

M = twarz, pieczęć.

Wydarzenie lub wydarzenie

W przypadkowym eksperymencie A wydarzenie Jest to występowanie lub nie określonego wyniku. Na przykład w przypadku uruchomienia waluty zdarzenie lub zdarzenie ma być drogie.

Może ci służyć: homologiczne strony

Kolejne zdarzenie w losowym eksperymencie może być następujące: że podczas premiery kości uwolniono liczbę mniej niż trzy.

Na wypadek, gdyby wydarzenie miało miejsce, zestaw możliwych wyników jest zestaw:

E = 1, 2, 3

Z kolei jest to podzbiór zestawu przestrzeni lub próbek:

M = 1, 2, 3, 4, 5, 6.

Przykłady

Poniżej znajdują się kilka przykładów, które ilustrują powyższe:

Przykład 1

Załóżmy, że dwie monety są rzucane, jeden po drugiej. Jest to żądane:

a) Wskaż, czy jest to losowy eksperyment, czy wręcz przeciwnie eksperyment deterministyczny.

b) Jaka jest przestrzeń próbki tego eksperymentu?

c) Wskaż całe zdarzenie A, odpowiadające eksperymentowi ma wynik twarzy i znaczków.

d) Obliczyć prawdopodobieństwo, że zdarzenie nastąpi.

e) Wreszcie, znajdź prawdopodobieństwo, że zdarzenie B: Nie pojawia się twarzą do wyniku.

Rozwiązanie 

a) Jest to przypadkowy eksperyment, ponieważ nie ma sposobu, aby przewidzieć, co będzie wynikiem uruchomienia dwóch monet.

b) Przestrzeń próbki jest zestawem wszystkich możliwych wyników:

S = (C, C), (C, s), (s, c), (s, s)

c) zdarzenie A, w podanym przypadku, może mieć następujące wyniki:

A = (c, s), (s, c)

d) Prawdopodobieństwo zdarzenia A jest uzyskiwane z podzielenia liczby elementów zestawu A między liczbą elementów zestawu odpowiadających przestrzeni próbki:

P (a) = 2/4 = ½ = 0.5 = 50%

e) Zestaw możliwych wyników odpowiadających zdarzeniu B (nie pojawiający się twarz w wyniku) jest:

Może ci służyć: Perfect Square Trinomial

B = (s, s)

Tak więc prawdopodobieństwo, że zdarzenie B występuje w eseju, jest stosunek między liczbą możliwych wyników B między liczbą liczby przypadków:

P (b) = ¼ = 0.25 = 25%.

Przykład 2

Torba zawiera 10 białych kulbaków i 10 czarnych kul. Z torby są losowo usuwani i nie patrząc na trzy kulki. 

a) Określ przestrzeń próbki tego losowego eksperymentu.

b) Określić zestaw wyników odpowiadających zdarzeniu, czyli to, że po eksperymencie są dwa czarne kulki.

c) zdarzenie B ma na celu uzyskanie co najmniej dwóch czarnych kulbowych, określić zestaw B wyników dla tego zdarzenia.

d) Jakie jest prawdopodobieństwo, że wydarzenie nastąpi?

e) Znajdź prawdopodobieństwo, że zdarzenie b.

f) Określ prawdopodobieństwo, że wynikiem losowego eksperymentu jest to, że co najmniej jeden czarny marmur. To wydarzenie zostanie nazwane C.

Rysunek 2. Czarne i czarne kulki do losowych eksperymentów. Źródło: Needpix.

Rozwiązanie

Aby zbudować przestrzeń próbki, przydatne jest wykonanie schematu drzewa, takiego jak ten pokazany na rycinie 3:

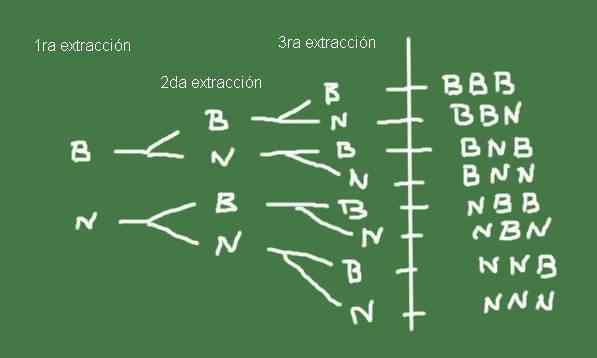Rysunek 3. Schemat drzewa na przykład 2. Przygotowane przez Fanny Zapata.

Zestaw ω możliwych wyników wyodrębnienia trzech kulbli z torby z taką samą liczbą czarnych i czarnych kulbaków jest dokładnie przestrzenią próbki tego losowego eksperymentu.

Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b), (n, b, n) , (n, n, b), (n, n, n)

Rozwiązanie b

Zestaw możliwych wyników odpowiadających zdarzeniu A, który polega na posiadaniu dwóch czarnych kulbaków, to:

Może ci służyć: suma riemann: historia, formuły i nieruchomości, ćwiczenia

A = (b, n, n), (n, b, n), (n, n, b)

Rozwiązanie c

Wydarzenie B jest zdefiniowane jako: „mieć co najmniej dwa czarne kulki po losowej ekstrakcji trzech z nich”. Zestaw możliwych wyników dla zdarzenia B to:

B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)

Rozwiązanie d

Prawdopodobieństwo posiadania zdarzenia A jest stosunkiem między liczbą możliwych wyników dla tego zdarzenia, a całkowitą liczbą możliwych wyników, to znaczy liczby elementów przestrzeni próbki.

P (a) = n (a) / n (ω) = 3/8 = 0.375 = 37.5%

Więc jest 37.5% prawdopodobieństwo posiadania dwóch czarnych kultur po losowym wyodrębnianiu trzech kulbaków z torby. Ale zauważ, że w żaden sposób nie możemy przewidzieć dokładnego wyniku eksperymentu.

Rozwiązanie e

Podane jest prawdopodobieństwo, że zdarzenie B, składające się z co najmniej jednego czarnego marmuru, wynosi:

P (b) = n (b) / n (ω) = 4/8 = 0.5 = 50%

Oznacza to, że możliwość zdarzenia B jest równa prawdopodobieństwu, które nie występuje. 

Rozwiązanie f

Prawdopodobieństwo uzyskania co najmniej jednego czarnego marmuru, po wydobyciu trzech z nich, jest równe 1 mniejsze prawdopodobieństwo, że wynik to „trzy białe kulki”.

P (c) = 1 - p (b b) = 1 - ⅛ = ⅞ = 0.875 = 87.5%

Teraz możemy zweryfikować ten wynik, zauważając, że liczba możliwości, biorąc pod uwagę zdarzenie C jest równa liczbie elementów możliwych wyników dla zdarzenia C:

C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)

N (c) = 7

P (c) = n (c) / n (ω) = ⅞ = 87.5%

Bibliografia

1. Canalphi. Losowy eksperyment. Odzyskane z: YouTube.com.
2. Mathemovil. Losowy eksperyment. Odzyskane z: YouTube.com
3. Pishro Nick h . Wprowadzenie do prawdopodobieństwa. Pobrano z: prawdopodobieństwoCourse.com
4. Ross. Prawdopodobieństwo i statystyki dla inżynierów. Mc-Graw Hill.
5. Wikipedia. Eksperyment (teoria prawdopodobieństwa). Źródło: w:.Wikipedia.com
6. Wikipedia. Zdarzenie deterministyczne. Odzyskane z: jest. Wikipedia.com
7. Wikipedia. Losowy eksperyment. Odzyskane z: jest.Wikipedia.com