Reguła empiryczna Jak to zastosować, po co jest rozwiązane

A Zasada empiryczna Jest to wynik praktycznego doświadczenia i obserwacji prawdziwego życia. Na przykład możesz wiedzieć, że gatunki ptaków można zaobserwować w niektórych miejscach o każdej porze roku i że można ustalić obserwację „reguły”, która opisuje cykle życia tych ptaków.

W statystykach reguła empiryczna odnosi się do formy grupowania obserwacji wokół wartości centralnej, średniej lub średniej, w odchyleniach standardowych.

Załóżmy, że masz grupę ludzi o średnim wysokości 1.62 metry i odchylenie standardowe 0.25 metrów, wówczas reguła empiryczna pozwoliłaby na zdefiniowanie, na przykład, ile osób byłoby w odstępie średniej, mniej lub bardziej odchyleniem standardowym?

Zgodnie z regułą 68% danych jest mniej więcej standardowym odchyleniem średniej, to znaczy 68% osób grupy będzie miało wysokość między 1.37 (1.62-0.25) i 1.87 (1.62+0.25) metry.

[TOC]

Skąd pochodzi rządy empiryczne?

Reguła empiryczna jest uogólnieniem twierdzenia Tchebyheva i rozkładu normalnego.

Twierdzenie Tchebysheva

Twierdzenie Tchebyheva mówi, że: Dla pewnej wartości k> 1 prawdopodobieństwo, że zmienna losowa jest jednym z średnich mniej k razy więcej niż odchylenie standardowe, a średni czas k razy, odchylenie standardowe jest większe lub równe (1-1 /k²).

Zaletą tego twierdzenia jest to, że dotyczy ono dyskretnych lub ciągłych zmiennych losowych z dowolnym rozkładem prawdopodobieństwa, ale reguła zdefiniowana z niego nie zawsze jest bardzo precyzyjna, ponieważ zależy od symetrii rozkładu rozkładu. Bardziej asymetryczna rozkład zmiennej losowej, mniej dostosowane do reguły będzie jej zachowaniem.

Reguła empiryczna zdefiniowana na podstawie tego twierdzenia to:

Jeśli k = √2, mówi się, że 50% danych jest w przedziale: [µ - √2 s, µ + √2 s]

Jeśli k = 2, mówi się, że 75% danych jest w przedziale: [µ - 2 s, µ + 2 s]

Jeśli k = 3, mówi się, że 89% danych jest w przedziale: [µ - 3 s, µ + 3 s]

Normalna dystrybucja

Rozkład normalny lub Bell Gauss pozwala ustalić regułę empiryczną lub regułą 68 - 95–99.7.

Może ci służyć: proporcja

Reguła opiera się na prawdopodobieństwie występowania zmiennej losowej w odstępach między średnią mniejszą, dwoma lub trzema odchyleniami standardowymi a średnim plus jeden, dwa lub trzy odchylenia standardowe.

Reguła empiryczna definiuje następujące przedziały:

68.27% danych jest w przedziale: [µ - s, µ + s]

95.45% danych jest w przedziale: [µ - 2s, µ + 2s]

99.73% danych jest w przedziale: [µ - 3s, µ + 3s]

Na rysunku widać, w jaki sposób te przedziały są prezentowane i związek między nimi poprzez zwiększenie szerokości bazy graficznej.

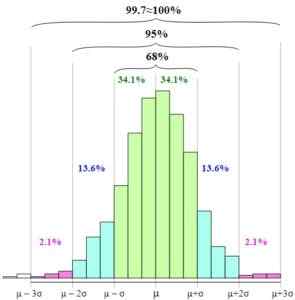Zasada empiryczna. Melilikamp [CC BY-SA 4.0 (https: // creativeCommons.org/)] Standaryzacja zmiennej losowej, to znaczy wyrażenie zmiennej losowej pod względem zmiennej standardowej lub normalnej, upraszcza użycie reguły empirycznej, ponieważ zmienna Z ma średnią równą zero, a odchylenie standardowe równe do jednego.

Dlatego zastosowanie reguły empirycznej w skali standardowej zmiennej normalnej z definiuje następujące przedziały:

68.27% danych jest w przedziale: [-1, 1]

95.45% danych jest w przedziale: [-2, 2]

99.73% danych jest w przedziale: [-3, 3]

Jak zastosować zasadę empiryczną?

Reguła empiryczna pozwala ci skrócić obliczenia podczas pracy z rozkładem normalnym.

Załóżmy, że grupa 100 studentów uniwersytetów ma średni wiek 23 lata, ze standardowym odchyleniem 2 lat. Na jakie informacje pozwala reguła empiryczna?

Zastosowanie reguły empirycznej implikuje wykonanie kroków:

1- Zbuduj interwały reguł

Ponieważ średnia wynosi 23, a odchylenie standardowe wynosi 2, wówczas interwały to:

[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]

[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]

[µ - 3s, µ + 3s] = [23–3 (2), 23 + 3 (2)] = [17, 29]

2- Obliczyć liczbę uczniów w każdym przedziale zgodnie z wartościami procentowymi

(100)*68.27% = 68 studentów w przybliżeniu

(100)*95.45% = około 95 studentów

(100)*99.73% = 100 studentów

3- Odstępy od wieków są powiązane z ilościami studentów i interpretowane

Co najmniej 68 studentów ma od 21 do 25 lat.

Może ci służyć: statystyka opisowa: historia, cechy, przykłady, koncepcje

Co najmniej 95 studentów ma od 19 do 27 lat.

Praktycznie 100 studentów ma od 17 do 29 lat.

Jaka jest reguła empiryczna?

Reguła empiryczna jest szybkim i praktycznym sposobem analizy danych statystycznych, ponieważ jest coraz bardziej wiarygodny w zakresie, w jakim rozkład jest zbliżony do symetrii.

Jego przydatność zależy od pola, w którym jest używany i pojawia się pytania. Bardzo przydatne jest wiedzieć, że występowanie wartości trzech odchyleń standardowych jest prawie mało prawdopodobne poniżej lub powyżej średniej, nawet w przypadku zmiennych rozkładu nieformalnych, co najmniej 88.8% przypadków znajduje się w przedziale trzech sigma.

W naukach społecznych ogólnie rozstrzygającym wynikiem jest przedział średniej więcej lub bardziej sigma (95%), podczas gdy w fizyce cząstek nowy efekt wymaga przedziału pięciu sigmas (99.99994%) należy uznać za odkrycie.

Rozwiązane ćwiczenia

Króliki w rezerwacie

W rezerwacie dzikiej przyrody szacuje się, że jest średnio 16.000 królików o odchyleniu standardowym 500 królików. Jeśli rozkład zmiennej „Liczba królików w rezerwacie” jest nieznana, czy to możliwe.000 i 17.000 królików?

Interwał można przedstawić w niniejszych Warunkach:

15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s

17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s

Dlatego: [15000, 17000] = [µ - 2 s, µ + 2 s]

Stosując twierdzenie Tchebyheva, istnieje prawdopodobieństwo co najmniej 0.75, że populacja królików rezerwatu przyrody wynosi między 15.000 i 17.000 królików.

Średnie dzieci z kraju

Średnia waga jednego -letniego dzieci jest zwykle rozłożona ze średnią 10 kilogramów i odchyleniem standardowym około 1 kilograma.

a) Oszacuj odsetek jednego dzieci w kraju, które mają średnią wagę od 8 do 12 kilogramów.

8 = 10 - 2 = 10 - 2 (1) = µ - 2 s

12 = 10 + 2 = 10 + 2 (1) = µ + 2 s

Dlatego: [8, 12] = [µ - 2s, µ + 2S]

Może ci służyć: Turs Tukey: Co to jest w przypadku przykładu rozwiązanego ćwiczenia

Zgodnie z regułą empiryczną można potwierdzić, że 68.27% dzieci w kraju ma od 8 do 12 kilogramów wagi.

b) Jakie jest prawdopodobieństwo znalezienia jednego -letniego dziecka o długości 7 kilogramów lub mniejszej wagi?

7 = 10 - 3 = 10 - 3 (1) = µ - 3 s

Wiadomo, że 7 kilogramów masy reprezentuje wartość µ - 3s, a także wiadomo, że 99.73% dzieci ma od 7 do 13 kilogramów masy. To pozostawia tylko 0.27% wszystkich dzieci dla skrajności. Połowa z nich, 0.135%, ma 7 kilogramów masy lub mniej, a druga połowa, 0.135%, ma 11 kilogramów wagi lub więcej.

Można więc stwierdzić, że istnieje prawdopodobieństwo 0.00135, że dziecko ma 7 kilogramów masy lub mniej.

c) Jeżeli populacja kraju osiągnie 50 milionów mieszkańców i dzieci z 1 roku?

9 = 10 - 1 = µ - s

11 = 10 + 1 = µ + s

Dlatego: [9, 11] = [µ - s, µ + s]

Zgodnie z regułą empiryczną, 68.27% jednego -letniego dzieci jest w przedziale [µ -s, µ + s]

W kraju jest 500 000 dzieci jednego roku (1% z 50 milionów), więc 341350 dzieci (68.27% z 500000) ma od 9 do 11 kilogramów masy.

Bibliografia

1. Abraira, v. (2002). Odchylenie standardowe i błąd standardowy. Magazyn Semergen. Web odzyskał.Archiwum.org.
2. Freund, r.; Wilson, w.; Mohr, d. (2010). Metody statystyczne. Trzeci wyd. Academic Press-Evevier Inc.
3. Alicante Server (2017). Reguła empiryczna (warunki statystyczne). Glosariusz odzyskano.Server-Alive.com.
4. Lind, d.; Marchal, w.; Wathen, s. (2012). Statystyki dotyczyły biznesu i gospodarki. Dziesiąty ed. McGraw-Hill/Inter-American z Meksyku S. DO.
5. Salinas, godz. (2010). Statystyki i prawdopodobieństwa. Odzyskane z UDA.Cl.
6. SAKAL, r.; Rohlf, f. (2009). Wprowadzenie do biostatystyki. Drugi wyd. Dover Publications, Inc.
7. Spiegel, m. (1976). Prawdopodobieństwo i statystyka. Seria Schaum. McGraw-Hill/Inter-American z Meksyku S. DO.
8. Spiegel, m.; Stephens, L. (2008). Statystyka. Czwarty ed. McGraw-Hill/Inter-American z Meksyku S. DO.
9. STAT119 Review (2019). Pytania empiryczne reguły rozwiązywania. Źródło: Stat119review.com.
10. (2019). 68-95-99.7 Zasada. Odzyskane z.Wikipedia.org.