Homocedyczność Czym jest, znaczenie i przykłady

 Homocedyczność W predykcyjnym modelu statystycznym występuje, jeśli we wszystkich grupach danych jednej lub więcej obserwacji, wariancja modelu w odniesieniu do zmiennych objaśniających (lub niezależnych) pozostaje stała.

Model regresji może być homokdastyczny lub nie, w którym to przypadku rozmawiamy heterocedyczność.

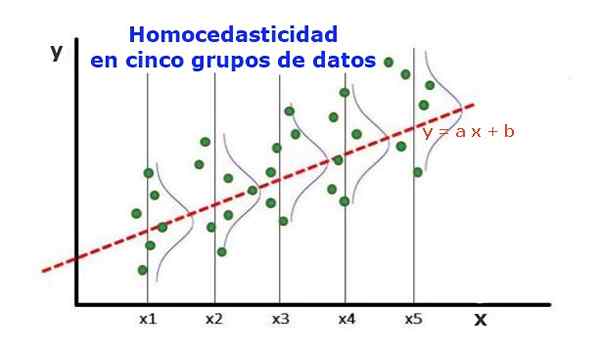
Rysunek 1. Pięć grup danych i regulacja regresji zestawu. Wariancja dotycząca przewidywanej wartości jest taka sama w każdej grupie. (Upav-unbrary.org)

Model regresji statystycznej kilku zmiennych niezależnych nazywany jest homocedastycznym, tylko wtedy, gdy wariancja przewidywanego błędu zmiennej (lub odchylenia standardowego zmiennej zależnej) pozostaje jednolita dla różnych grup zmiennych objaśniających lub niezależnych.

W pięciu grupach danych na rycinie 1 wariancja została obliczona w każdej grupie, w odniesieniu do wartości oszacowanej przez regresję, obracając się na taką samą w każdej grupie. Zakłada się również, że dane podążają za rozkładem normalnym.

Na poziomie graficznym oznacza to, że punkty są równo rozproszone lub rozproszone wokół przewidywanej wartości przez regulację regresji, a model regresji ma ten sam błąd i ważność dla zakresu zmiennej objaśniającej.

[TOC]

Znaczenie homokedyczności

Aby zilustrować znaczenie homokedastyczności w statystykach predykcyjnych, konieczne jest kontrast z przeciwnym zjawiskiem, heterocedycznością.

Homocedastyczność w porównaniu z heterocedycznością

W przypadku ryc. 1, w którym występuje homokedyczność, spełnia się, że:

Var ((y1-y1); x1) ≈ var ((y2-y2); x2) ≈ ... var (y4-y4); x4)

Gdzie var ((yi-ii); xi) reprezentuje wariancję, para (xi, yi) reprezentuje fakt grupy I, podczas gdy yi jest wartością przewidującą regresję średniej wartości xi grupy. Wariancja danych grupy I jest obliczana w następujący sposób:

Var ((yi -ii); xi) = ∑j (yij - yi)^2/n

Przeciwnie, gdy występuje heterokedyczność, model regresji może nie być ważny dla całego regionu, w którym został obliczony. Rysunek 2 pokazuje przykład tej sytuacji.

Może ci służyć: jakie są wewnętrzne alternatywne kąty? (Z ćwiczeniami)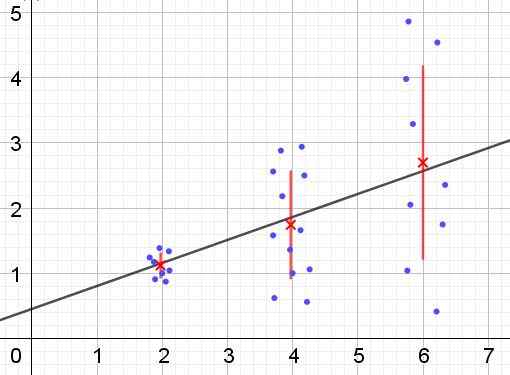 Rysunek 2. Grupa danych, która ma heterokedyczność. (Własne opracowanie)

Na rycinie 2 trzy grupy danych i zestaw zestawu są reprezentowane przez regresję liniową. Należy zauważyć, że dane w drugiej i w trzeciej grupie są bardziej rozproszone niż w pierwszej grupie. Wykres z ryc. 2 pokazuje również średnią wartość każdej grupy i jej pasek błędu ± σ, będąc odchyleniem standardowym σ każdej grupy danych. Należy pamiętać, że odchylenie standardowe σ jest pierwiastkiem kwadratowym wariancji.

Oczywiste jest, że w przypadku heterocedyczności błąd oszacowania regresji zmienia się w zakresie wartości zmiennej objaśniającej lub niezależnej, a w przedziałach, w których błąd jest bardzo duży, przewidywanie przez regresję jest niewiarygodne lub nie dotyczy.

W modelu regresji błędy lub odpady (y -y) muszą być rozmieszczone z równą wariancją (σ^2) w przedziale wartości zmiennych niezależnych. Z tego powodu dobry model regresji (liniowy lub nieliniowy) musi przejść test homocedastyczności. 

Testy homocedyczności

Punkty pokazane na rycinie 3 odpowiadają danymi badania, które dąży do związku między cenami (w dolarach) domów w zależności od wielkości lub obszaru w metrach kwadratowych.

Pierwszym modelu, który jest przećwiczony, jest regresja liniowa. Po pierwsze, zauważa się, że współczynnik determinacji R^2 regulacji jest dość wysoki (91%), więc można uznać, że regulacja jest zadowalająca.

Jednak dwa regiony można wyraźnie odróżnić od wykresu regulacji. Jeden z nich, ten po prawej zamkniętej w owalnym, spotyka homocedastyczność, podczas gdy region lewicy nie ma homocedastyczności.

Może ci służyć: stopień wielomianu: jak jest to ustalone, przykłady i ćwiczenia

Oznacza to, że przewidywanie modelu regresji jest odpowiednie i niezawodne w zakresie od 1800 m^2 do 4800 m^2, ale bardzo nieodpowiednie poza tym regionem. W obszarze heterokedycznym nie tylko błąd jest bardzo duży, ale także dane wydają się podążać za innym trendem inną niż zaproponowany przez model regresji liniowej.

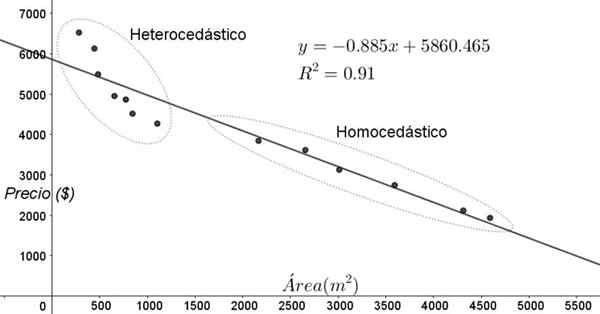Rysunek 3. Ceny mieszkań w porównaniu z obszarem i modelem predykcyjnym według regresji liniowej, pokazującymi obszary homocedastyczności i heterocedyczności. (Własne opracowanie)

Wykres dyspersji danych jest najprostszym i najbardziej wizualnym testem ich homocedastyczności, jednak czasami nie jest tak widoczny, jak na przykładzie pokazanym na rycinie 3, konieczne jest uciekania się do grafiki ze zmiennymi pomocniczymi.

Znormalizowane zmienne

W celu oddzielenia obszarów, w których spełnia się homocedastyczność, w których nie wprowadza się znormalizowane zmienne ZRES i ZREDED:

ZRES = ABS (y - y)/σ

Zpred = y/σ

Należy zauważyć, że zmienne te zależą od zastosowanego modelu regresji, ponieważ jest to wartość przewidywania regresji. Poniżej znajduje się wykres dyspersji ZRES vs ZRED dla tego samego przykładu:

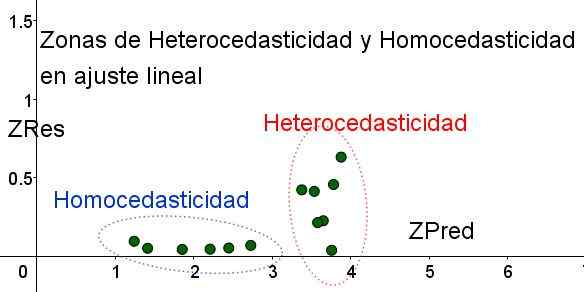Rysunek 4. Należy zauważyć, że w strefie homocedastyczności ZRES pozostaje jednolity i niewielki w regionie prognozy (własne opracowanie).

Na wykresie na rycinie 4 ze znormalizowanymi zmiennymi obszar, w którym błąd resztkowy jest mały, a jednolity jest wyraźnie oddzielony, w odniesieniu do tego, który nie. W pierwszym obszarze homocedastyczność jest wypełniona, podczas gdy błąd resztkowy jest bardzo zmienny i duży.

Dostosowanie regresji jest stosowane do tej samej grupy danych 3. Wynik pokazano na poniższym rysunku:

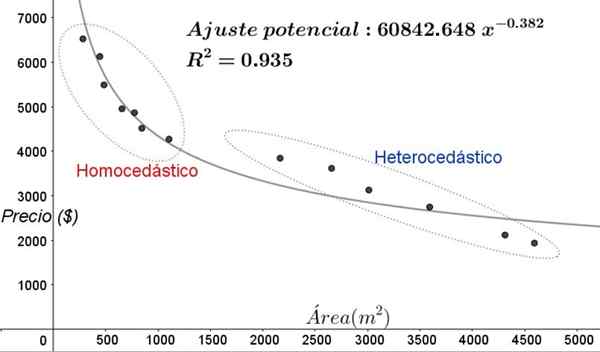Rysunek 5. Nowe obszary homocedastyczności i heterocedyczności w dostosowaniu danych za pomocą modelu regresji niewidalnej. (Własne opracowanie).

Na wykresie na rycinie 5 należy wyraźnie zauważyć obszary homocedic i heterokedicastyczne. Należy również zauważyć, że obszary te zostały wymienione w odniesieniu do tych, które zostały utworzone w modelu liniowego dostosowania.

Może ci służyć: rodzaje kątów, cechy i przykłady

Na wykresie na rycinie 5 widać, że nawet gdy istnieje współczynnik określenia korekty dość wysoki (93,5%), model nie jest odpowiedni dla całego przedziału zmiennej objaśniającej, ponieważ dane dla wartości starszych niż 2000 M^2 mają heterocedastyczność.

Niefograficzne testy homocedastyczności

Jednym z najczęściej używanych testów nieognograficznych w celu sprawdzenia, czy homocedastyczność jest spełniona jest Test Breusch-Pagana.

Wszystkie szczegóły tego testu nie zostaną podane w tym artykule, ale jego podstawowe cechy i ich etapy są szeroko opisane:

1. Model regresji jest stosowany do danych N, a wariancja tego samego jest obliczana w odniesieniu do wartości oszacowanej przez model σ^2 = ∑J (yj - y)^2/n.
2. Zdefiniowana jest nowa zmienna ε = ((yj - y)^2) / (σ^2)
3. Ten sam model regresji jest stosowany do nowej zmiennej, a jej nowe parametry regresji są obliczane.
4. Ustalana jest wartość krytyczna kwadratu chi (χ^2), ponieważ jest to połowa sumy kwadratów nowych odpadów w zmiennej ε.
5. Stosuje się tabelę rozkładu kwadratowego ChI, biorąc pod uwagę poziom istotności na osi x (zwykle 5%) i liczbę stopni swobody (#OF zmienne regresji z wyjątkiem jednostki), aby uzyskać wartość tablicy.
6. Wartość krytyczna uzyskana w kroku 3 jest porównywana z wartością znalezioną w tabeli (χ^2).
7. Jeśli wartość krytyczna znajduje się poniżej wartości tabeli, masz hipotezę zerową: istnieje homokedyczność
8. Jeśli wartość krytyczna jest powyżej wartości tabeli, masz alternatywną hipotezę: nie ma homokedastyczności.

Większość statystycznych pakietów komputerowych, takich jak: SPSS, Minitab, R, Python Pandas, SAS, Statgraphic i kilka innych zawiera test homocedastyczności Breusch-Pagan. Kolejny test weryfikacji jednolitości wariancji Test Levene.

Bibliografia

1. Box, Hunter & Hunter. (1988) Statystyki dla naukowców. Odwróciłem redaktorów.
2. Johnston, J (1989). Metody ekonometryki, redakcje Vicens -ise.
3. Murillo i González (2000). Podręcznik ekonomiczny. University of Las Palmas de Gran Canaria. Źródło: UlpGC.Jest.
4. Wikipedia. Homocedyczność. Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Homoscedastyczność. Źródło: w:.Wikipedia.com