Hipergeometryczne wzory rozkładu, równania, model

Rozkład hipergeometryczny Jest to dyskretna funkcja statystyczna, odpowiednia do obliczenia prawdopodobieństwa w losowych eksperymentach z dwoma możliwymi wynikami. Warunkiem wymaganym do zastosowania jest to, że są to małe populacje, w których ekstrakcje nie są wymieniane, a prawdopodobieństwa nie są stałe. 

Dlatego, gdy wybrany jest element populacji, aby poznać wynik (prawda lub fałsz) pewnej cechy, ten sam element nie można ponownie wybrać.

Rysunek 1. W populacji takich śrub istnieją z pewnością wadliwe okazy. Źródło: Pixabay.

Z pewnością następny wybrany element jest zatem bardziej skłonny do uzyskania prawdziwego wyniku, jeśli poprzedni element miał wynik ujemny. Oznacza to, że prawdopodobieństwo różni się, w zakresie, w jakim elementy próbki są wyodrębnione.

Główne zastosowania rozkładu hipergeometrycznego to: kontrola jakości w procesach o niewielkiej populacji i obliczanie prawdopodobieństwa w losowych grach.

Jeśli chodzi o funkcję matematyczną, która definiuje rozkład hipergeometryczny, składa się z trzech parametrów, które są:

- Liczba elementów populacji (N)

- Rozmiar próbki (M) 

- Liczba zdarzeń w pełnej populacji z korzystnym (lub niekorzystnym) wynikiem badanego charakterystyki (N).

[TOC]

Wzory i równania

Formuła rozkładu hipergeometrycznego daje prawdopodobieństwo P o czym X Występują korzystne przypadki pewnej cechy. Sposób pisania matematycznego, w zależności od liczb kombinatorycznych, jest:

W poprzednim wyrażeniu N, N I M Są parametry i X sama zmienna. 

-Całkowita populacja to N.

-Liczba pozytywnych wyników pewnej binarnej cechy w odniesieniu do całkowitej populacji to N.

-Liczba elementów próbki to M.

W tym przypadku, X Jest to losowa zmienna, która wymaga wartości X I P (x) wskazuje prawdopodobieństwo wystąpienia X sprzyjające przypadki badań charakterystyki.

Ważne zmienne statystyczne

Inne zmienne statystyczne dla rozkładu hipergeometrycznego to:

- Połowa μ = m*n/n

- Zmienność σ^2 = M*(N/N)*(1-N/N)*(N-M)/(N-1)

- Typowe odchylenie σ który jest pierwiastkiem kwadratowym wariancji.

Model i właściwości 

Aby dostać się do modelu rozkładu hipergeometrycznego, opiera się na prawdopodobieństwie uzyskania X korzystne przypadki w próbce wielkości M. Ta próbka zawiera elementy, które spełniają badaną nieruchomość i elementy, które nie.

Pamiętajmy o tym N reprezentuje liczbę korzystnych przypadków w całkowitej populacji N rzeczy. Wówczas prawdopodobieństwo zostanie obliczone w ten sposób:

Może ci służyć: przestrzeń wektorowa: podstawa i wymiar, aksjomaty, właściwości

P (x) = (# sposobów na uzyskanie x# w nieudane sposoby)/(# Total Hays of Vlecting)

Wyrażając powyższe w postaci liczb kombinatorycznych, osiągnięty jest następujący model rozkładu prawdopodobieństwa:

Główne właściwości rozkładu hipergeometrycznego

Są następujące:

- Próbka musi być zawsze mała, chociaż populacja jest duża.

- Elementy próbki są wyodrębnione z jednego, bez ponownego włączania ich do populacji.

- Nieruchomość, którą należy zbadać, jest binarna, to znaczy może przyjmować tylko dwie wartości: 1 albo 0, O Cóż PRAWDA albo podróbka.

Na każdym etapie ekstrakcji prawdopodobieństwo zmienia się w zależności od poprzednich wyników.

Podejście przez rozkład dwumianowy

Inną właściwością rozkładu hipergeometrycznego jest to, że można podchodzić do rozkładu dwumianowego, oznaczonego jako Bi, Tak długo, jak populacja N być duży i co najmniej 10 razy większy niż próbka M. W takim przypadku byłoby tak:

P (n, n, m; x) = bi (m, n/n, x)           

Tak długo, jak N jest duże i n> 10 m

Przykłady

Przykład 1

Załóżmy, że maszyna, która wytwarza śruby i skumulowane dane, wskazuje, że 1% wychodzi z defektami. Następnie w polu n = 500 śrub liczba defektów będzie:

N = 500 * 1/100 = 5

Prawdopodobieństwa poprzez rozkład hipergeometryczny

Załóżmy, że z tego pudełka (to znaczy tej populacji) bierzemy próbkę M = 60 śrub.

Prawdopodobieństwo, że żadna śruba (x = 0) próbka liści wadliwa, wynosi 52,63%. Ten wynik jest osiągany przy użyciu funkcji rozkładu hipergeometrycznego:

P (500, 5, 60; 0) = 0,5263

Prawdopodobieństwo, że x = 3 śruby próbki pozostawiają wadliwe, wynosi: P (500, 5, 60; 3) = 0,0129.

Z drugiej strony prawdopodobieństwo, że x = 4 śruby z sześćdziesiątej próbki opuściły wadliwe, wynosi: P (500, 5, 60; 4) = 0,0008.

Wreszcie prawdopodobieństwo, że x = 5 śrub w tej próbce wychodzi z defektem: P (500, 5, 60; 5) = 0.

Ale jeśli chcesz znać prawdopodobieństwo, że w tej próbce istnieją więcej niż 3 wadliwe śruby, należy uzyskać skumulowane prawdopodobieństwo, dodając:

P (3)+P (4)+P (5) = 0,0129+0,0008+0 = 0,0137.

Ten przykład pokazano na rycinie 2, uzyskane przez użycie Geogebra Bezpłatne oprogramowanie w szkołach, instytutach i uniwersytetach.

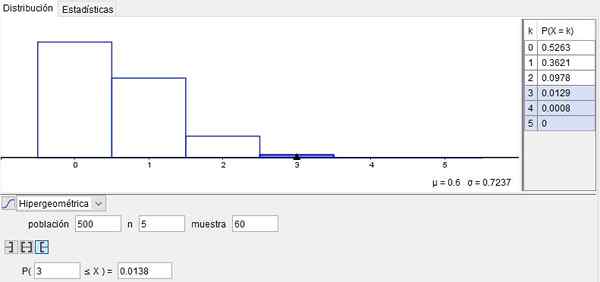Rysunek 2. Przykład rozkładu hipergeometrycznego. Przygotowane przez f. Zapata z Geogebra.

Przykład 2

Hiszpański pokład ma 40 kart, z czego 10 ma złoto, a pozostałe 30 nie ma tego. Załóżmy, że z tej talii wyodrębniono 7 kart, które nie wracają na pokład.

Może ci służyć: centralna symetria: właściwości, przykłady i ćwiczenia

Jeśli x jest liczbą złota obecnych w 7 wyodrębnionych kartach, wówczas prawdopodobieństwo, że są x oros w ekstrakcji 7 kart, jest podawany przez rozkład hipergeometryczny P (40,10,7; x).

Spójrzmy na to: Aby obliczyć prawdopodobieństwo posiadania 4 złota w ekstrakcji 7 kart, używamy wzoru rozkładu hipergeometrycznego z następującymi wartościami:

A wynik to: prawdopodobieństwo 4,57%.

Ale jeśli chcesz poznać prawdopodobieństwo uzyskania więcej niż 4 kart, będziemy musieli dodać:

P (4)+P (5)+P (6)+P (7) = 5,20%

Rozwiązane ćwiczenia

Poniższy zestaw ćwiczeń ma na celu zilustrowanie i asymilowanie pojęć, które zostały przedstawione w tym artykule. Ważne jest, aby czytelnik próbował je rozwiązać samodzielnie, zanim spojrzał na rozwiązanie.

Ćwiczenie 1

Fabryka profilaktyczna odkryła, że ​​na każde 1000 prezerwatyw wytwarzanych przez określoną maszynę 5 jest wadliwy. Aby przeprowadzić kontrolę jakości, 100 prezerwatyw jest losowo pobranych, a działka jest odrzucana, jeśli jest co najmniej jeden lub więcej wadliwych. Odpowiedź:

a) Jaka możliwość musi być odrzucona 100 partii?

b) Czy to kryterium kontroli jakości są wydajne?

Rozwiązanie

W tym przypadku pojawią się bardzo duże liczby kombinatoryczne. Obliczenia są trudne, chyba że dostępny jest odpowiedni pakiet komputerowy.

Ale ponieważ jest to duża populacja, a próbka jest dziesięć razy mniejsza niż całkowita populacja, możesz zastosować podejście do rozkładu hipergeometrycznego z powodu rozkładu dwumianowego:

P (1000,5,100; x) = Bi (100, 5/1000, x) = BI (100, 0.005, x) = c (100, x)*0.005^x (1-0.005)^(100-x)

W poprzednim wyrażeniu C (100, x) Jest to liczba kombinatoryczna. Wówczas prawdopodobieństwo Haya więcej niż jeden wadliwy zostanie obliczony w następujący sposób:

P (x> = 1) = 1 - bi (0) = 1-.6058 = 0.3942

Jest to doskonałe podejście, w porównaniu z wartością uzyskaną przy stosowaniu rozkładu hipergeometrycznego: 0.4102

Można powiedzieć, że 40% prawdopodobieństwa wielu 100 profilaktyki należy odrzucić, co nie jest bardzo wydajne.

Ale będąc nieco mniej wymagającym w procesie kontroli jakości i odrzucaniu.

Ćwiczenie 2

Plastikowa maszyna taco działa w taki sposób, że na 10 sztuk, jeden jest zdeformowany. W 5 -osobowej próbce ta możliwość musi być wadliwy jeden kawałek.

Rozwiązanie

Populacja: n = 10

Może ci służyć: tożsamości pitagorejskie: demonstracja, przykład, ćwiczenia

Liczba n wadliwy dla każdego n: n = 1

Rozmiar próbki: M = 5

P (10, 1, 5; 1) = C (1,1)*C (9,4)/C (10,5) = 1*126/252 = 0.5

Dlatego istnieje 50% prawdopodobieństwo, że w próbce 5, taco wychodzi zdeformowane.

Ćwiczenie 3

Na spotkaniu młodych szkół średnich jest 7 kobiet i 6 dżentelmenów. Wśród dziewcząt, 4 studiów humanistycznych i 3 nauki. W grupie chłopców 1 studiuje nauk humanistycznych i 5 nauki. Oblicz następujące:

a) losowo wybieranie trzech dziewcząt: jakie są prawdopodobieństwo, że wszystkie nauka humanistyki?.

b) Jeśli trzech uczestników zostanie wybranych losowo na spotkanie przyjaciół: jakie są trzy z nich, niezależnie od seksu, studiuj te trzy lub humanistyczne, a także wszystkich trzech?.

c) Wybierz teraz dwóch przypadkowych przyjaciół i zadzwoń X do losowej zmiennej „liczba osób, które badają humanistykę”. Spośród dwóch wybranych, określ średnią lub oczekiwaną wartość X i wariancja σ^2.

Rozwiązanie 

Populacja to całkowita liczba dziewcząt: n = 7. Osoby studiujące humanistyczne wynoszą n = 4, całości. Losowa próbka dziewcząt wynosi M = 3.

W takim przypadku prawdopodobieństwo, że trzy są humanistyczne, jest podawane przez funkcję hipergeometryczną:

P (n = 7, n = 4, m = 3, x = 3) = c (4, 3) c (3, 0) / c (7, 3) = 0.1143

Potem jest 11.4% prawdopodobieństwo, że trzy losowe chicas badają humanistyczne.

Rozwiązanie b

Wartości do użycia to:

-Populacja: n = 14

-Ilość, która bada litery to: n = 6 i

-Rozmiar próbki: M = 3.

-Liczba przyjaciół studiujących humanistykę: x

Zgodnie z tym x = 3 oznacza, że ​​trzy badania humanistyczne, ale x = 0 oznacza, że ​​nikt nie bada nauk humanistycznych. Prawdopodobieństwo, że trzy badanie to samo jest podane przez sumę:

P (14, 6, 3, x = 0) + P (14, 6, 3, x = 3) = 0.0560 + 0.1539 = 0.2099

Następnie mamy 21% prawdopodobieństwo, że trzech uczestników spotkań, wybranych losowo, studiuje to samo.

Rozwiązanie c

Tutaj mamy następujące wartości:

N = 14 Całkowita populacja przyjaciół, n = 6 Całkowita liczba w populacji, która badała humanistykę, wielkość próbki wynosi M = 2.

Nadzieja to:

E (x) = m * (n/n) = 2 * (6/14) = 0.8572

I wariancja:

σ (x)^2 =  M*(N/N)*(1-N/N)*(N-M)/(N-1) = 2*(6/14)*(1-6/14)*(14-2)/(14 -1) =

= 2*(6/14)*(1-6/14)*(14-2)/(14-1) = 2*(3/7)*(1-3/7)*(12) (13)  = 0.4521

Bibliografia

1. Dyskretne rozkłady prawdopodobieństwa. Odzyskane z: Biploot.usal.Jest
2. Statystyki i prawdopodobieństwo. Rozkład hipergeometryczny. Źródło: ProjectOdescartes.org
3. CDPYE-UGR. Rozkład hipergeometryczny. Odzyskane z: Ugr.Jest
4. Geogebra. Klasyczny Geogebra, obliczanie prawdopodobieństwa. Odzyskane z Geogebry.org
5. Łatwy spadek. Rozwiązane ćwiczenia rozkładu hipergeometrycznego. Odzyskany z: probafacil.com
6. Minitab. Rozkład hipergeometryczny. Źródło: wsparcie.Minitab.com
7. University of Vigo. Główne dyskretne rozkłady. Odzyskany z: anapg.strony internetowe.Uvigo.Jest
8. Porozienie. Statystyki i kombinatoryczne. Pobrano z: Viciputor.internet
9. Weisstein, Eric W. Rozkład hipergeometryczny. Odzyskane z: Mathworld.Wolfram.com
10. Wikipedia. Rozkład hipergeometryczny. Odzyskane z: jest.Wikipedia.com