Ile ma osi symetrii ma koło?
- 2513
- 724
- Eliasz Dubiel
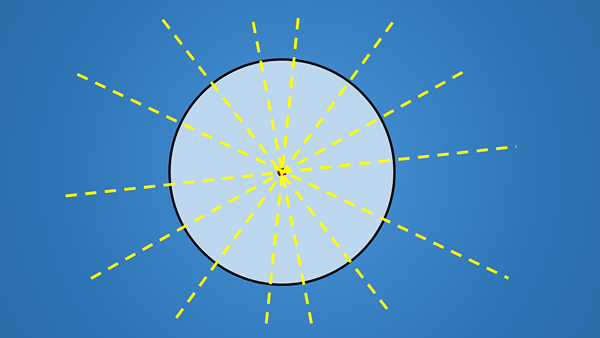
Osie symetrii koła Są nieskończone. Te osie to te podzielone dowolny kształt geometryczny na dwie dokładnie te same połówki. A okrąg składa się ze wszystkich punktów, których odległość do punktu stałego jest mniejsza lub równa pewnej wartości „R”.
Stały punkt wspomniany powyżej nazywa się środkiem, a wartość „R” nazywa się radio. Radio jest największą odległością między punktem w kręgu i środku.
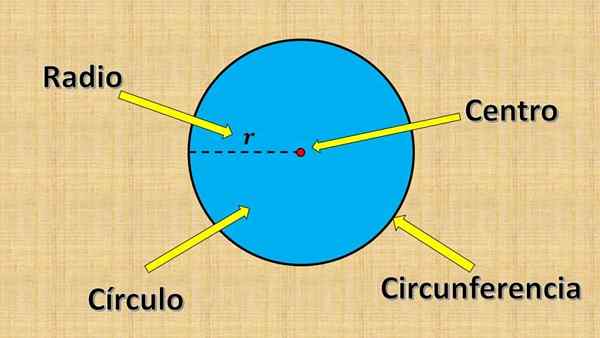
Z drugiej strony każdy segment linii, którego końce znajdują się na krawędzi koła (obwód) i który przechodzi przez środek, nazywa się średnicą. Jego miara jest zawsze równa dwukrotności radia.
Okrąg i obwód
Nie myl okręgu z obwodem. Obwód odnosi się tylko do punktów, które znajdują się w odległości „R” środka; to znaczy tylko krawędź koła.
Jednak szukając osi symetrii, jest to obojętne, jeśli pracujesz z obwodem lub z okrągiem.
Jaka jest oś symetrii?
Oś symetrii to linia, która dzieli pewną liczbę geometryczną na dwie równe części. Innymi słowy, oś symetrii działa jak lustro.
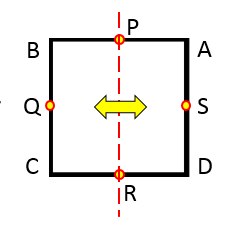 Na poprzednim obrazie można zauważyć, że linia pionowa, która przechodzi przez środek przeciwnych stron kwadratu, jest osą symetrii tego samego.
Na poprzednim obrazie można zauważyć, że linia pionowa, która przechodzi przez środek przeciwnych stron kwadratu, jest osą symetrii tego samego.
Osie symetrii koła
Jeśli obserwuje się jakikolwiek okrąg, niezależnie od jego promienia, można zauważyć, że nie każda prosta, która go przecina, jest osą symetrii.
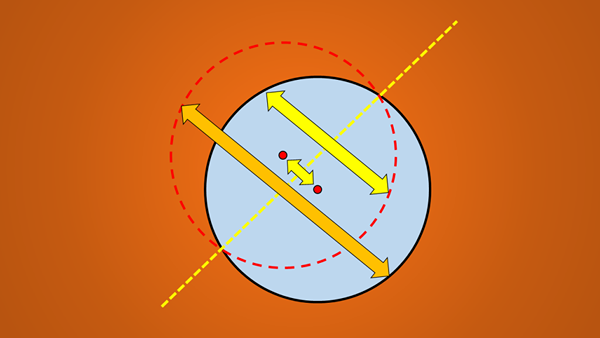
Może ci służyć: metoda Trachtenberga: co to jest, przykładyNa przykład żadna z linii narysowanych na poniższym obrazie nie jest osi symetrii.
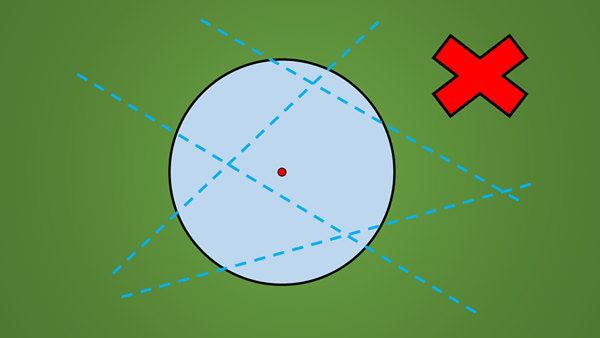
Łatwym sposobem sprawdzenia, czy linia jest osi symetrii, czy nie, jest prostopadle odzwierciedlająca liczbę geometryczną po przeciwnej stronie linii.
Jeśli odbicie nie pasuje do pierwotnej figury, wspomniana linia nie jest osiem symetrii. Na poniższym obrazie ilustrują tę technikę.
Ale jeśli rozważany jest następujący obraz, notoryczne jest, że linia narysowana jest osi symetrii koła.
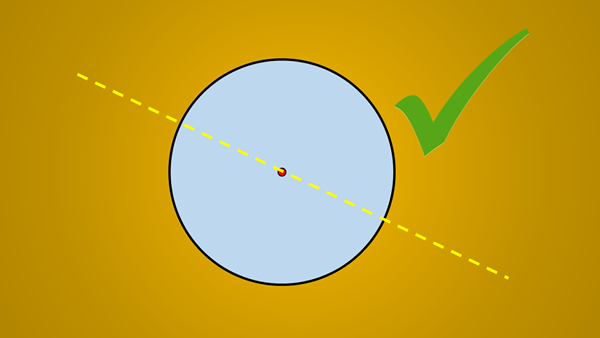
Pytanie brzmi: czy jest więcej osi symetrii? Odpowiedź brzmi tak. Jeśli ta linia 45 ° jest obracana w sensie anty -horarycznym, uzyskana linia jest również osi symetrii koła.
To samo dzieje się, jeśli 90 °, 30 °, 8 i, ogólnie, dowolna liczba stopni.
Ważną rzeczą w tych liniach nie jest skłonność, jaką mają, ale wszyscy przechodzą przez środek koła. Dlatego każda linia zawierająca średnicę koła jest osiem symetrii.
Ponieważ okrąg ma nieskończoną ilość średnic, ma nieskończoną ilość osi symetrii.
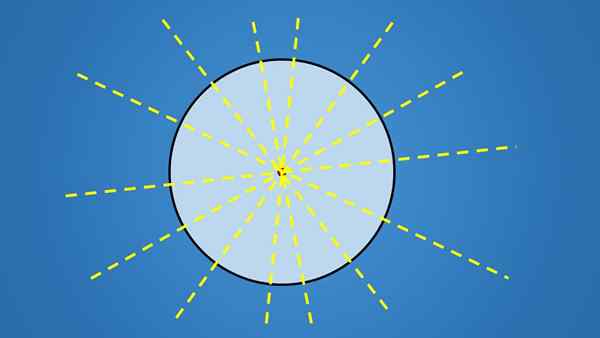
Inne figurki geometryczne, takie jak trójkąt, czworobok, pięciokąt, sześciokąt lub jakikolwiek inny wielokąt, mają skończoną ilość osi symetrii.
Powodem, dla którego koło ma nieskończoną ilość osi symetrii, jest to, że nie ma stron.
- « Równoważne zestawy, jakie są wyjaśnienie, przykłady
- Względni kuzyni, co to są, wyjaśnienie, przykłady »

