Względni kuzyni, co to są, wyjaśnienie, przykłady

Jest nazywany względni kuzyni ). Innymi słowy, dwie liczby relatywne są kuzynami względnymi, jeśli w ich rozpadzie w liczbach pierwotnych, nie mają wspólnego czynnika.

Na przykład, jeśli wybrane są 4 i 25, rozkład w czynnikach pierwszych każdego z nich wynoszą odpowiednio 22 i 5². Jak widać, nie mają one żadnego wspólnego czynnika, dlatego 4 i 25 są względnymi kuzynami.

Z drugiej strony, jeśli wybierzesz 6 i 24, podczas dokonywania rozpadu czynników pierwszych uzyskuje się, że 6 = 2*3 i 24 = 23*3.

Jak widać, te dwa ostatnie wyrażenia mają co najmniej jeden wspólny czynnik, dlatego nie są względnymi kuzynami.

Charakterystyka względnych kuzynów

Szczegóły, z którymi musi opiekować się.

Z drugiej strony powyższa definicja można podsumować w następujący sposób: dwie liczby całkowite „A” i „B” są względnymi kuzynami, i tylko maksymalnym wspólnym dzielnikiem z nich jest 1, to znaczy MCD (A, B. ) = 1.

Dwa bezpośrednie wnioski z tej definicji to:

-Jeśli „A” (lub „B”) jest liczbą pierwszą, to MCD (A, B) = 1.

-Jeśli „A” i „B” są liczbami pierwszymi, to MCD (A, B) = 1.

To znaczy, jeśli przynajmniej jedna z wybranych liczb jest liczbą pierwszą, wówczas para liczb są względnymi kuzynami.

Inne funkcje

Inne wyniki zastosowane do ustalenia, czy dwie liczby są względnymi kuzynami: to:

-Jeśli dwie liczby całkowe są kolejne, to są to względni kuzyni.

-Dwie liczby naturalne „A” i „B” są względnymi kuzynami, i tylko jeśli liczby ”(2^a) -1" i „(2^b) -1” są względnymi kuzynami.

-Dwie liczby całkowe „A” i „B” są względnymi kuzynami, jeśli i tylko wtedy, gdy wykresuje punkt (a, b) w płaszczyźnie kartezjańskim i budują linię przechodzącą przez pochodzenie (0,0) i (a (a , b), nie zawiera żadnego punktu z całymi współrzędnymi.

Przykłady

1.- Rozważ liczby całe 5 i 12. Rozkłady w pierwszych czynnikach obu liczb to odpowiednio: 5 i 2²*3. Podsumowując, MCD (5,12) = 1, zatem 5 i 12 są względnymi kuzynami.

2.- Niech liczby -4 i 6. Następnie -4 = -2² i 6 = 2*3, tak że MCD (-4,6) = 2 ≠ 1. Podsumowując -4 i 6 nie są względnymi kuzynami.

Jeśli linia, która przechodzi przez uporządkowane pary (-4,6) i (0,0) oraz w celu ustalenia równania wspomnianej linii, można zweryfikować, że przechodzi to przez punkt (-2,3).

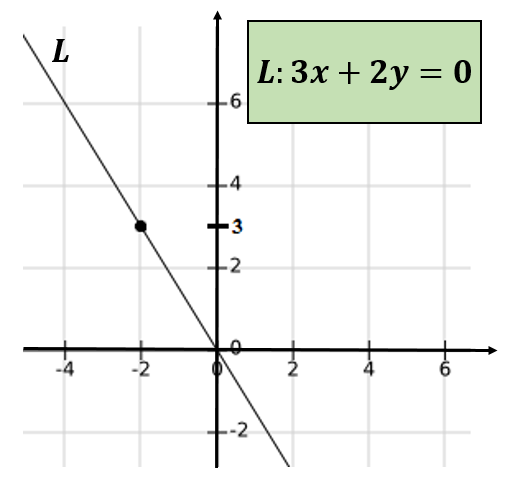
Ponownie stwierdzono, że -4 i 6 nie są względnymi kuzynami.

3.- Liczby 7 i 44 są względnymi kuzynami i można je szybko zakończyć dzięki tym, co zostało powiedziane powyżej, ponieważ 7 jest liczbą główną.

4.- Rozważ liczby 345 i 346. Będąc dwiema kolejnymi liczbami, weryfikuje się, że MCD (345 346) = 1, dlatego 345 i 346 są względnymi kuzynami.

5.- Jeśli uwzględniono liczby 147 i 74, to są to względne kuzyny, ponieważ 147 = 3*7² i 74 = 2*37, dlatego MCD (147,74) = 1.

6.- Liczby 4 i 9 są względnymi kuzynami. Aby to zademonstrować, możesz użyć drugiej wspomnianej powyżej charakterystyki. Rzeczywiście, 2^4 -1 = 16-1 = 15 i 2^9-1 = 512-1 = 511.

Otrzymane liczby to 15 i 511. Rozkłady w podstawowych czynnikach tych liczb wynoszą odpowiednio 3*5 i 7*73, tak że MCD (15 511) = 1.

Jak widać, użycie drugiej charakterystyki jest dłuższą i bardziej pracochłonną pracą, aby zweryfikować ją bezpośrednio.

7.- Rozważ liczby -22 i -27. Wtedy te liczby można przepisać w następujący sposób: -22 = -2*11 i -27 = -3³. Dlatego MCD (-22, -27) = 1, więc -22 i -27 są względnymi kuzynami.