Sferyczne współrzędne przykłady i ćwiczenia rozwiązane

współrzędne sferyczne Są one układem lokalizacji punktowej w trzech wymiarach przestrzeni składającej się z współrzędnych promieniowych i dwóch współrzędnych kątowych zwanych współrzędną polarną i współrzędną azymutową.

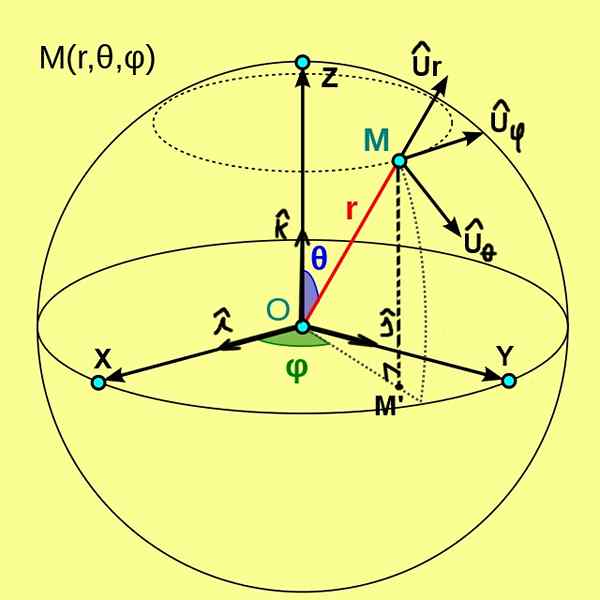
Na rycinie 1, które widzimy poniżej, pokazano współrzędne sferyczne (r, θ, φ) punktu m. Współrzędne te są skierowane do ortogonalnego systemu osi kartezjańskich X, Y, Z pochodzenia lub.

Rysunek 1. Współrzędne sferyczne (r, θ, φ) z punktu m. (Wikimedia Commons)

W takim przypadku współrzędna R punktu M jest odległością od tego punktu do pochodzenia lub. Współrzędna polarna θ reprezentuje kąt między dodatnią osiem półprzewodnikowym a promieniem wektora OM. Podczas gdy współrzędna azymutalna φ jest kątem między pozytywną osiem półprzewodnikowym a promieniem wektora OM ', będąc m' ortogonalnym rzutem m na płaszczyźnie xy.

Współrzędna promieniowa r przyjmuje tylko wartości dodatnie, ale jeśli punkt znajduje się przy pochodzeniu, to r = 0. Współrzędna polarna θ bierze jako minimalną wartość 0º dla punktów znajdujących się na dodatnim półroczu. Wreszcie, współrzędna azymutalna φ bierze jako minimalną wartość 0º i maksymalny poziom 360º.

0 ≤ r < ∞

0 ≤ θ ≤ 180º

0 ≤ φ  < 360º

[TOC]

Zmiana współrzędnych

Następnie podane zostaną wzory, które umożliwiają współrzędne kartezjańskie (x, y, z) punktu m, zakładając, że współrzędne sferyczne tego samego (r, θ, φ) punkt:

x = r sen (θ) cos (φ)

y = r sen (θ) sin (φ) 

Z = r cos (θ)

W ten sam sposób warto znaleźć relacje, aby przejść od współrzędnych kartezjańskich (x, y, z) punktu podanego do kulistych współrzędnych tego punktu:

R = √ (x^2 + y^2 + z^2)

θ = arcan (√ (x^2 + y^2) / z)

Może ci służyć: dyskretna zmienna losowa

φ = arctan (y / x)

Podstawa wektorowa we współrzędnych sferycznych

Od współrzędnych sferycznych definiuje się ortonormalną podstawę wektorów podstawowych, które są oznaczone przez Ur, Uθ, Uφ. Rysunek 1 pokazuje te trzy wektory jednostkowe, które mają następujące cechy:

- Ur Jest to styczna wektora jednostkowego do linii promieniowej θ = ctte i φ = ctte;

- Uθ Jest to wektor styczny jednostkowy do łuku φ = ctte i r = ctte;

- Uφ Jest to jednolite styczne wektorowe do łuku r = ctte i θ = ctte.

Elementy linii i objętości we współrzędnych sferycznych

Pozycja wektorowa punktu w przestrzeni we współrzędnych sferycznych jest napisana w ten sposób:

R = r Ur

Ale nieskończenie małe zmienność lub przemieszczenie punktu w przestrzeni trójwymiarowej, we współrzędnych wyraża ją następująca relacja wektorowa:

DR = Dr Ur + R dθ Uθ + r sen (θ) dφ Uφ

Wreszcie, napisany jest nieskończenie małej objętości we współrzędnych sferycznych:

dv = r^2 sin (θ) Dr dθ dφ

Te relacje są bardzo przydatne do obliczania całek linii i objętości w sytuacjach fizycznych, które mają kulistą symetrię.

Związek ze współrzędnymi geograficznymi

Rozumie się współrzędne geograficzne, że służą one do lokalizacji miejsc na powierzchni ziemi. Ten system wykorzystuje współrzędne szerokości i długości do zlokalizowania pozycji na powierzchni ziemi.

W geograficznym układzie współrzędnych powierzchnia Ziemi ma.

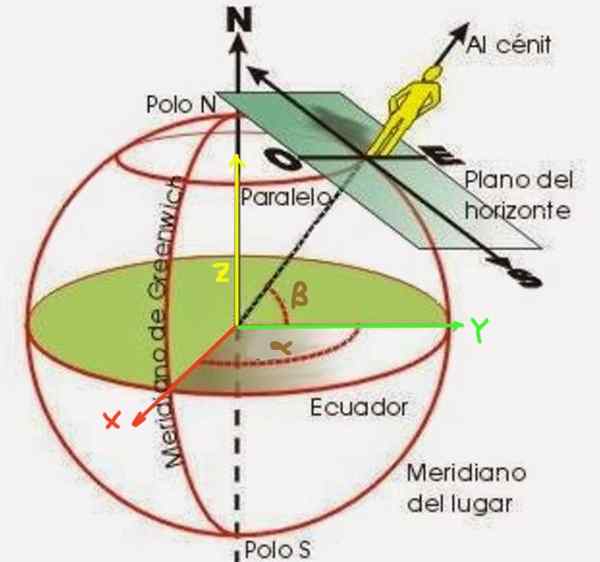Rysunek 2. Długość szerokości α i β obserwatora na powierzchni Ziemi.

Szerokość β jest kątem utworzonym przez promień, który zaczyna się od środka ziemi do punktu, w którym chcesz ustawić. Jest mierzony z płaszczyzny równikowej, jak pokazano na rycinie 2. Z drugiej strony długość α jest kątem, który południk punktu, który umieszcza formę w odniesieniu do zerowego południka (znanego jako Meridian Greenwich).

Może ci służyć: wartość względna

Szerokość geograficzna może być szerokością północną lub południową, w zależności od tego, czy miejsce, które się znajdują, znajduje się na półkuli północnej, czy na półkuli południowej. Podobnie długość może być zachód, czy to w zależności od tego, czy lokalizacja jest zachodnia, czy na wschód od zerowego południka.

Formuły do ​​zmiany z geograficznych na sferyczne

Aby uzyskać te wzory, pierwszą rzeczą jest ustanowienie układu współrzędnych. Płaszczyzna XY jest wybierana zbieżna z płaszczyzną równikową, będąc dodatnim pół -osi X, który przechodzi od środka ziemi i przez zerowy południk. Z kolei oś i przechodzi przez 90º i południkę. Powierzchnia ziemi ma radio RT.

Z tym układem współrzędnych są zatem transformacje geograficzne na sferyczne:

αeβn → (RT, θ = 90º-β, φ = α)

αOβN → (RT, θ = 90º-β, φ = 360º-α)

αEβ → (RT, θ = 90º+β, φ = α)

αOβS → (RT, θ = 90º+β, φ = 360º-α) 

Przykłady

Przykład 1

Geograficzne współrzędne Palma de Mallorca (Hiszpania) to:

Długość Wschodu 38 847º i szerokość północna 39 570º. Aby określić sferyczne współrzędne odpowiadające Palmie de Mallorca, zastosowano pierwszy z wzorów poprzednich wzorów rozdziału:

38 847ºE39,570ºN → (R = 6371 km, θ = 90º-39,570º, φ = 38 847º)

Wówczas współrzędne sferyczne to:

Palma de Mallorca: (r = 6371 km, θ = 50,43º, φ = 38,85º)

W poprzedniej odpowiedzi R równa średniemu promieniu Ziemi.

Przykład 2

Wiedząc, że Wyspy Falkland (Falkland) mają współrzędne geograficzne 59ºO 51,75ºS, określ odpowiednie współrzędne polarne. Pamiętaj, że oś x przechodzi od środka ziemi do południka 0º i na płaszczyźnie równikowej; Oś y również w płaszczyźnie równikowej i przez 90º West Meridian; Wreszcie oś Z na osi obrotu naziemnego w kierunku południowym i północnym.

Może ci służyć: ograniczenie: definicja, typy, formuły, na przykład, na przykład

Aby znaleźć odpowiednie współrzędne sferyczne, używamy wzorów przedstawionych w poprzedniej sekcji:

59ºO 51,75ºS → (r = 6371 km, θ = 90º+51,75º, φ = 360º-59º) to znaczy

Malvinas: (r = 6371 km, θ = 141,75º, φ = 301º)

Ćwiczenia

Ćwiczenie 1

Znajdź karteńskie współrzędne Palma de Mallorca w systemie referencyjnym Cartesiano XYZ pokazanym na rycinie 2.

Rozwiązanie: Wcześniej w przykładzie 1 współrzędne sferyczne uzyskano na podstawie geograficznych współrzędnych Palma de Mallorca. Tak, że przedstawione powyżej formuły mogły być użyte do przemieszczania się z kulistej do kartezjan:

x = 6371 km Sen (50,43º) cos (38,85º)

Y = 6371 km Sen (50,43º) Sen (38,85º) 

Z = 6371 km cos (50,43º)

Wykonanie odpowiednich obliczeń to:

Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)

Ćwiczenie 2

Znajdź karteńskie współrzędne wysp Falkland w systemie referencyjnym Cartesiano XYZ pokazanym na rycinie 2.

Rozwiązanie: Wcześniej w przykładzie 2 Współrzędne sferyczne uzyskano na podstawie współrzędnych geograficznych Wysp Falklandzkich. Tak, że przedstawione powyżej formuły mogły być użyte do przemieszczania się z kulistej do kartezjan:

x = 6371 km Sen (141,75º) cos (301º)

y = 6371 km Sen (141,75º) Sen (301º) 

Z = 6371 km CO (141,75º)

Uzyskuje się odpowiednie obliczenia:

Wyspy Falkland: (x = 2031 km, y = -3381 km, z = -5003)

Bibliografia

1. Arfken G i Weber H. (2012). Metody matematyczne dla fizyków. Kompleksowy przewodnik. 7. edycja. Academic Press. ISBN 978-0-12-384654-9
2. Obliczenie CC. Rozwiązane cylindryczne i sferyczne problemy współrzędnych. Odzyskane z: Obliczanie.DC
3. Warsztaty astronomii. Szerokość i długość geograficzna. Źródło: stawka.Blogspot.com/
4. Weisstein, Eric W. „Współrzędne sferyczne.”Z Mathworld-A Wolfram Web. Odzyskane z: Mathworld.Wolfram.com
5. Wikipedia. Sferyczny układ współrzędnych. Źródło: w:.Wikipedia.com
6. Wikipedia. Pola wektorowe we współrzędnych cylindrycznych i sferycznych. Źródło: w:.Wikipedia.com