Prostokątne współrzędne przykłady i ćwiczenia rozwiązane

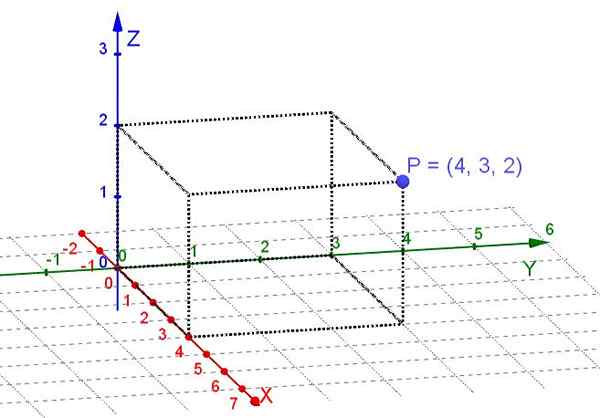
Prostokątne współrzędne o Kartezjanie są te, które są uzyskiwane, gdy są rzutowane ortogonalnie na trzech osiach kartezjańskich X, Y, Z Punkt zlokalizowany w przestrzeni trójwymiarowej.

Osie kartezjańskie są prostopadłe proste. W systemie współrzędnych kartezjańskich trzy rzeczywiste liczby, które są jego prostokątnymi współrzędnymi, są przypisywane do każdego punktu w przestrzeni.

Rysunek 1. Prostokątne współrzędne punktu P (własne opracowanie)

Samolot jest podprzestrzenią trójwymiarowej przestrzeni. W przypadku rozważenia punktów w płaszczyźnie wystarczy wybrać parę prostopadłych osi x i jako system kartezjański. Wtedy w każdym punkcie w samolocie przypisano mu dwie liczby rzeczywiste, że jego prostokątne współrzędne są.

[TOC]

Pochodzenie prostokątnych współrzędnych

Prostokątne współrzędne zostały pierwotnie zaproponowane przez francuskiego matematyka René Descartes (1596 i 1650), dlatego otrzymują wyznanie kartezjan.

Z tą ideą Kartezjusza punkty płaszczyzny i przestrzeni są przypisane liczby, tak że liczby geometryczne związały się z równaniem algebraicznym, a klasyczne twierdzenia geometryczne można wykazać algebraicznie. Z współrzędnymi kartezjańskimi narodziła się geometria analityczna.

Samolot kartezjański

Jeśli na płaszczyźnie wybrane są dwie prostopadłe linie, które przecinają się w jednym punkcie lub; a jeśli również każdą linię przypisuje się kierunek i skalę liczbową między kolejnymi punktami równoległymi, istnieje system kartezjański lub plan, w którym każdy punkt płaszczyzny jest powiązany z uporządkowaną parą dwóch liczb rzeczywistych, które są odpowiednio jej projekcjami na osie x i y.

Punkty a = (3, 2); B = (-2, 3); C = (-2, -3) i D = (3, -3) są reprezentowane w płaszczyźnie kartezjańskiej, jak pokazano poniżej:

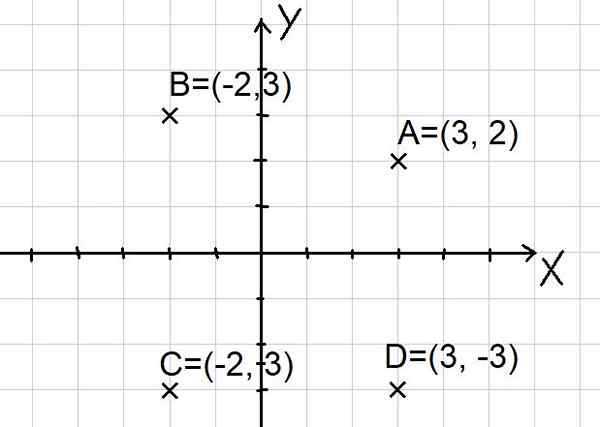Rysunek 2. Punkty na płaszczyźnie kartezjańskim. (Własne opracowanie)

Zauważ, że dwie osie x i y dzielą płaszczyznę na cztery sektory zwane kwadrantami. Punkt A znajduje się w pierwszej ćwiartce, B w drugiej ćwiartce, C w trzecim ćwiartce i punkt D w czwartym ćwiartce.

Może ci służyć: populacja i próbka

Odległość między dwoma punktami

Odległość między dwoma punktami a i b płaszczyzny kartezjańskiej jest długością segmentu, który je jednoczy. Odległość tę można obliczyć analitycznie w następujący sposób:

D (a, b) = √ (bx - ax)^2 + (przez - ay)^2)

Formuła przednia uzyskuje się przez zastosowanie twierdzenia Pitagorasa.

Zastosowanie wspomnianej formuły do ​​punktów A, B na ryc. 2 to:

D (a, b) = √ (-2 - 3)^2 + (3 - 2)^2) = √ (-5)^2 + 1^2) = √ (26)

To znaczy, że d (a, b) = 5,10 jednostki. Zauważ, że odległość uzyskano bez potrzeby pomiaru z zasadą, zastosowano całkowicie algebraiczną procedurę.

Analityczna ekspresja linii

Prostokątne współrzędne umożliwiają analityczną reprezentację podstawowych obiektów geometrycznych, takich jak punkt i linia. Dwa punkty a i b definiują jedną linię. Nachylenie linii jest definiowane jako iloraz między różnicą we współrzędnych a punktem B mniejszym, podzielony przez różnicę we współrzędnych punktu B mniej A:

w toku = (przez - ay)/(bx - ax)

Dowolny punkt współrzędnych (x, y), który należy do linii (AB), musi mieć to samo zbocze:

oczekuje = (y - ay)/(x - ax)

Równanie uzyskane przez równość zboczów jest analityczna lub algebraiczna reprezentacja linii, która przechodzi przez punkty A i B:

(y - ay)/(x - ax) = (przez - ay)/(bx - ax).

Jeśli jesteś zabrany za a i b, prostokątne współrzędne z ryc. 2 to:

(Y - 2)/(x - 3) = (3 - 2)/( - 2 - 3)

(y - 2)/(x - 3) = -⅕

W tym konkretnym przypadku znajduje się linia z ujemnym nachyleniem -⅕, co oznacza, że ​​znajduje się w punkcie linii i zwiększając współrzędną X w jednostce, współrzędna i zmniejsza się w 0,2 jednostek. 

Może ci służyć: toroid lub toro dona

Najbardziej typowym sposobem napisania równania linii w płaszczyźnie jest współrzędna i czysta jako funkcja zmiennej x:

y = -(1/5) x + 13/5 

Przykłady

Przykład 1

Uzyskaj metodami analitycznymi Odległość między punktami C i A, będąc prostokątnymi współrzędnymi C = (-2, -3) i A = A = (3.2).

Formuła euklidesowej odległości między tymi dwoma punktami jest napisana w ten sposób:

D (a, c) = √ ((cx - ax)^2 + (cy - ay)^2)

Zastępując odpowiednie prostokątne współrzędne, które masz:

D (a, c) = √ (-2-3)^2 + (-3-2)^2) = √ (-5)^2 + (-5)^2) = 5√2 = 7,07

Przykład 2

Uzyskaj równanie linii, która przechodzi przez punkt C współrzędnych (-2, -3) i punkt P współrzędnej (2, 0).

Po pierwsze, uzyskuje się nachylenie linii CP:

oczekuje = (0 -(-3)) / (2 -( -2)) = ¾ 

Dowolny punkt q ogólnych współrzędnych prostokątnych (x, y), który należy do linii CP, musi mieć to samo nachylenie:

oczekuje = (y -(-3)) / (x -( -2)) = (y +3) / (x +2)

To znaczy, że równanie linii CP jest:

(Y +3) / (x +2) = ¾

Alternatywnym sposobem napisania równania linii CP jest oczyszczenie i:

y = ¾ x - 3/2 

Rozwiązane ćwiczenia

Ćwiczenie 1

Uzyskaj prostokątne współrzędne punktu przecięcia między liniami y = - (1/5) x + 13/5 i linia y = ¾ x - 3/2.

Rozwiązanie: Z definicji punkt przecięcia dwóch linii ma te same prostokątne współrzędne. Dlatego współrzędne i w punkcie skrzyżowania są identyczne dla obu linii:

-(1/5) x + 13/5 = ¾ x - 3/2

Co prowadzi do następującego wyrażenia:

Może ci służyć: prostokątne trapez: właściwości, relacje i wzory, przykłady

(¾ + ⅕) x = 13/5 +3/2

Uzyskuje się rozwiązywanie suma ułamków:

19/20 x = 41/10

Clearing X:

x = 82/19 = 4,32

Aby uzyskać wartość i przecięcie, wartość X uzyskana w jednej z linii jest zastąpiona:

y = ¾ 4,32 - 3/2 = 1,74

Oznacza to, że podane linie są przechwycone w punkcie I współrzędnych i = (4,32; 1,74).

Ćwiczenie 2

Uzyskaj równanie obwodu, które przechodzi przez prostokątny punkt współrzędnych R (3, 4) i ma centrum u pochodzenia współrzędnych.

Rozwiązanie: Radio R jest odległością od punktu R do pochodzenia lub współrzędnych (0, 0).

d (r, o) = √ ((rx - 0)^2 + (ry - 0)^2) = √ ((3 - 0)^2 + (4 - 0)^2) = √ (3^2 + 4^2) = √ (9 + 16) = √ (25) = 5

Oznacza to, że jest to promień 5 okrąg 5 wyśrodkowany na (0,0).

Dowolny punkt p (x, y) obwodu musi mieć tę samą odległość 5 do środka (0, 0) dla tego, co można zapisać:

D (p, o) = √ ((x - 0)^2 + (y - 0)^2) = √ (x^2 + y^2) = 5

To jest do powiedzenia:

√ (x^2 + y^2) = 5

Aby wyeliminować pierwiastek kwadratowy, obaj członkowie równości pozostają cicho:

x^2 + y^2 = 25

Jakie jest równanie obwodu.

W tym przykładzie zilustrowano moc prostokątnego układu współrzędnych, co pozwala określić obiekty geometryczne, takie jak obwód bez konieczności użycia papieru, ołówka i kompasu. Określono obwód wymagany tylko metodami algebraicznymi.

Bibliografia

1. Arfken G i Weber H. (2012). Metody matematyczne dla fizyków. Kompleksowy przewodnik. 7. edycja. Academic Press. ISBN 978-0-12-384654-9
2. Obliczenie CC. Prostokątne współrzędne rozwiązały problemy. Odzyskane z: Obliczanie.DC
3. Weisstein, Eric W. "Współrzędne kartezjańskie.”Z Mathworld-A Wolfram Web. Odzyskane z: Mathworld.Wolfram.com
4. Wikipedia. Kartezjański układ współrzędnych. Źródło: w:.Wikipedia.com