Natychmiastowa definicja prędkości, wzór, obliczenia i ćwiczenia

chwilowa prędkość Jest zdefiniowany jako chwilowa zmiana przemieszczenia w czasie. Jest to koncepcja, która dodaje wielkiej precyzji badań nad ruchem. I jest to postęp w odniesieniu do średniej prędkości, której informacje są bardzo ogólne.

Aby uzyskać chwilową prędkość, spójrzmy na tak mały odstęp czasowy. Rachunek różnicowy jest idealnym narzędziem do matematycznego wyrażania tej idei.

Natychmiastowa prędkość uwzględnia prędkość mobilną w każdym punkcie trasy. Źródło: Pixabay.

Punktem początkowym jest średnia prędkość:

Teraz podejdźmy do 0 do 0 wszystkiego, co może. Jest to limit, a wynik będzie dokładnie szybkość chwilowej:

Ten limit jest znany pod nazwą pochodnej. W notacji różnicowego rachunku: masz:

Pod warunkiem, że ruch jest ograniczony do linii prostej, można go wydać z notacją wektorową.

[TOC]

Obliczanie natychmiastowej prędkości: interpretacja geometryczna

Poniższy rysunek pokazuje geometryczną interpretację koncepcji pochodnej: jest to nachylenie linii tangens Do krzywej x (t) vs. T W każdym punkcie.

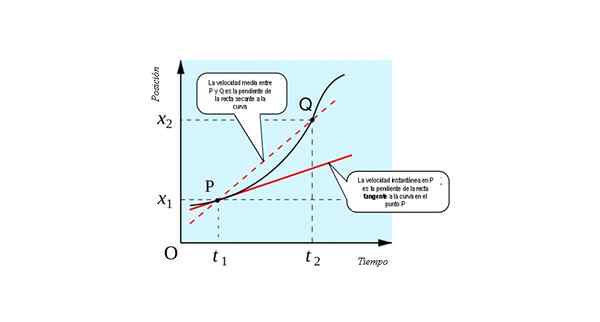Natychmiastowa prędkość w P równoważna liczbowo z nachyleniem linii stycznej do krzywej x vs. T w punkcie p. Źródło: Źródło: すじにく シチュー [CC0].

Możesz sobie wyobrazić, jak uzyskać limit, jeśli punkt Q stopniowo zbliża się. Nadejdzie czas, kiedy oba punkty będą tak blisko, że jeden nie można odróżnić od drugiego.

Linia, która je łączy, będzie suszyć (prosto, która przecina na dwa punkty), aby być styczna (prosto, która dotyka krzywej w jednym punkcie). Dlatego, aby znaleźć chwilową prędkość cząstki mobilnej, powinniśmy mieć:

• Wykres położenia cząstki w funkcji czasu. Znalezienie nachylenia stycznej linii do krzywej w każdej chwili, masz chwilową prędkość w każdym punkcie zajmowanym przez cząstkę.

Może ci służyć: prawo Ampère: formuła i równania, demonstracja, ćwiczenia

O Cóż:

• Funkcja pozycji cząstek X (t), który pochodzi w celu uzyskania funkcji prędkości V (t), wtedy ta funkcja jest oceniana za każdym razem T, Wygoda. Funkcja pozycji ma być pochodna.

Niektóre szczególne przypadki w obliczaniu chwilowej prędkości

-Nachylenie stycznej linii do krzywej w P wynosi 0. Null Slope oznacza, że ​​telefon komórkowy jest zatrzymany i że jego prędkość oczywiście wynosi 0.

-Nachylenie stycznej linii do krzywej w P jest większe niż 0. Prędkość jest dodatnia. Na powyższym wykresie oznacza to, że telefon komórkowy odchodzi od lub.

-Nachylenie stycznej linii do krzywej w P jest mniejsze niż 0. Prędkość byłaby ujemna. Na powyższym wykresie nie ma takich punktów, ale w takim przypadku zbliża się cząstka lub.

-Nachylenie stycznej linii do krzywej jest stałe w P i wszystkich innych punktach. W tym przypadku wykres jest linią prostą, a telefon komórkowy Jednolity ruch linii MRU (jego prędkość jest stała).

Ogólnie rzecz biorąc, funkcja V (t) Jest to również funkcja czasowa, która z kolei może wyprowadzić. Co jeśli nie można było znaleźć tych pochodzących z funkcji X (t) I V (t)?

W przypadku X (t) Możliwe, że nachylenie - szybkość chwilowej - ostro zmieniła znaki. Lub to natychmiast przejdzie z zera do innej wartości.

Jeśli tak, grafika X (t) Przedstawiłoby to wskazówki lub narożniki na nagłe zmiany. Bardzo różni się od przypadku reprezentowanego na poprzednim obrazie, na którym krzywa X (t) Jest to miękka krzywa, bez punktów, zakrętów, nieciągłości lub nagłych zmian.

Może ci służyć: kondensat Bose Einstein

Prawda jest taka, że ​​w przypadku prawdziwych telefonów komórkowych miękkie krzywe są tymi, które najlepiej reprezentują zachowanie obiektu.

Ogólny ruch jest dość złożony. Mobile można na chwilę zatrzymać, przyspieszyć, aby przejść od odpoczynku, aby uzyskać prędkość i uciec od punktu początkowego, zachowaj prędkość przez chwilę, a następnie zatrzymać się, aby ponownie zatrzymać się, a tym samym styl.

Mogą zacząć od nowa i kontynuować w tym samym kierunku. Lub działaj w niepowodzeniu i powrót. Nazywa się to różnorodnym ruchem w wymiarze.

Poniżej niektóre przykłady obliczenia prędkości chwilowej wyjaśnią zastosowanie danych definicji:

Rozwiązane natychmiastowe ćwiczenia prędkości

Ćwiczenie 1

Cząstka porusza się po linii prostej z następującym prawem ruchu:

x (t) = -t³ + 2 t² + 6 T - 10

Wszystkie jednostki są w systemie międzynarodowym. Znajdować:

a) Położenie cząstki w t = 3 sekundy.

b) Średnia prędkość w przedziale między t = 0 s i t = 3 s.

c) Średnia prędkość w przedziale między t = 0 s i t = 3 s.

d) chwilowa prędkość cząstki poprzedniego pytania, przy t = 1 s.

Odpowiedzi

a) Aby znaleźć pozycję cząstki, prawo ruchu (funkcja pozycji) przy t = 3:

x (3) = (-4/3).3³ + 2. 3² ₊ 6.3 - 10 m = -10 m

Nie ma problemu, że pozycja jest ujemna. Znak (-) wskazuje, że cząstka znajduje się po lewej stronie pochodzenia lub.

b) W obliczeniach średniej prędkości końcowe i początkowe położenia cząstki są wymagane we wskazanych czasach: x (3) i x (0). Pozycja przy t = 3 to x (3) i jest znana o poprzednim wyniku. Pozycja przy t = 0 sekund wynosi x (0) = -10 m.

Może ci służyć: statyczne: historia, jakie badania, aplikacje, prawa

Ponieważ pozycja końcowa jest taka sama jak początkowa, natychmiast stwierdza się, że średnia prędkość wynosi 0.

c) Średnia prędkość jest przyczyną pomiędzy przebytą odległością a czasem spędzonym. Teraz odległość jest modułem lub wielkością przemieszczenia, dlatego:

Odległość = | x2 - x1 | = | -10-(-10) | M = 20 m

Zauważ, że przebyta odległość jest zawsze pozytywna.

v_{M = 20 m/3 s = 6.7 m/s}

d) Tutaj konieczne jest znalezienie pierwszej pochodnej pozycji dotyczącej czasu. Następnie jest oceniany dla t = 1 sekunda.

x '(t) = -4 t² + 4 T + 6

x '(1) = -4.1² + 4.1 + 6 m/s = 6 m/s

Ćwiczenie 2

Poniżej znajduje się wykres pozycji telefonu komórkowego w funkcji czasu. Znajdź prędkość chwilową przy t = 2 sekundy.

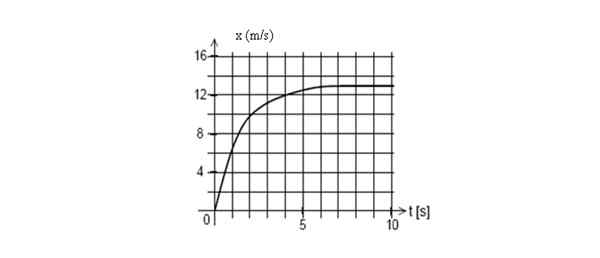Wykres pozycjonowania w porównaniu do czasu na telefon komórkowy. Źródło: Self Made.

Odpowiedź

Narysuj linię styczną do krzywej w t = 2 sekundy, a następnie oblicz nachylenie, biorąc dwa punkty linii.

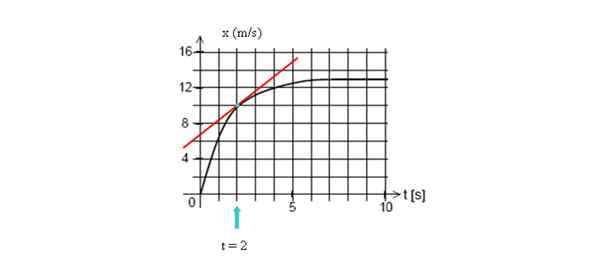Aby obliczyć prędkość chwilową we wskazanym punkcie, narysuj linię styczną do tego punktu i znajdź jej nachylenie. Źródło: Self Made.

W tym przykładzie weźmiemy dwa punkty, które można łatwo wizualizować, których współrzędne to (2 s, 10 m) i cięcie osi pionowej (0 s, 7 m):

Bibliografia

1. Giancoli, zm. Fizyka. Zasady z aplikacjami. 6^th Wydanie. Prentice Hall. 22-25.
2. Resnick, r. (1999). Fizyczny. Tom 1. Trzecie wydanie po hiszpańsku. Meksyk. Continental Editorial Company S.DO. c.V. 21-22.
3. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7^mama. Wydanie. Meksyk. Redaktorzy edukacyjni Cengage. 23-25.