Prędkość areolowa sposób, w jaki jest obliczane i rozwiązane ćwiczenia

Prędkość areolowa Jest to obszar zamiatania na jednostkę czasu i jest stały. Jest to typowe dla każdej planety i wynika z opisu drugiego prawa Keplera w sposób matematyczny. W tym artykule wyjaśnimy, czego się składa i jak jest obliczany.

Boom, który reprezentuje odkrycie planet poza Układem Słonecznym, reaktywował zainteresowanie ruchem planetarnym. Nic nie wierzy, że te planety egzo przestrzegają przepisów innych niż znane i ważne dla układu słonecznego: prawa Keplera.

Johannes Kepler był astronomem, który bez pomocy teleskopu i używanie obserwacji jego mentora Tycho Brahe, stworzył model matematyczny, który opisuje ruch planet wokół Słońca.

Opuścił ten model wyrażony w trzech prawach, które noszą jego imię i które pozostają tak ważne dzisiaj, jak w 1609 r., Kiedy ustanowił pierwsze dwa i 1618.

[TOC]

Prawa Keplera

W obecnym języku trzy prawa Keplera mówią w ten sposób:

1. Orbity wszystkich planet są eliptyczne, a słońce jest w centrum uwagi.

2. Wektor położenia, który przechodzi od słońca na planetę, przepływa równe obszary w równych czasach.

3. Plac okresu orbitalnego planety jest proporcjonalny do sześcian.

Planeta będzie miała prędkość liniową, jak każdy znany obiekt, który się porusza. I jest więcej: pisząc drugie prawo Keplera w formie matematycznej, pojawia się nowa koncepcja zwana prędkością Areolar, typowa dla każdej planety.

Dlaczego planety poruszają się eliptycznie po słońcu?

Ziemia i inne planety poruszają się po słońcu dzięki temu, że wywiera na nich siłę: przyciąganie grawitacyjne. To samo dotyczy każdej innej gwiazdy i planet, które są zgodne z twoim systemem, jeśli je masz.

Może ci służyć: wrażliwe ciepło: koncepcja, formuły i ćwiczenia rozwiązane

Jest to siła typu zwanego siłą centralną. Waga jest centralną siłą, z którą wszyscy są zaznajomieni. Obiekt, który wywiera siłę centralną, czy to słońce, czy odległa gwiazda, przyciąga planety w kierunku ich centrum i poruszają się opisując zamkniętą krzywą.

Zasadniczo krzywa ta może być przybliżona jako obwód, jak Nicolás Copernico, polski twórca astronomu teorii heliocentrycznej, zrobił to.

Odpowiedzialna siła to przyciąganie grawitacyjne. Siła ta zależy bezpośrednio od mas gwiazdy i planety, o której mowa i jest odwrotnie proporcjonalna do kwadratu odległości, który je oddziela.

Problem nie jest taki łatwy, ponieważ w Układzie Słonecznym wszystkie elementy oddziałują w ten sposób, dodając złożoność sprawy. Nie są również cząsteczkami, ponieważ gwiazdy i planety mają mierzalny rozmiar.

Z tego powodu centralny punkt orbity lub obwodu przeżyty przez planety nie jest dokładnie wyśrodkowany na gwiazdzie, ale na punkcie zwanym środkiem grawitacji systemu planety Sol-Planet.

Powstała orbita jest eliptyczna. Poniższy obraz pokazuje, biorąc jako przykład Ziemia i Słońca:

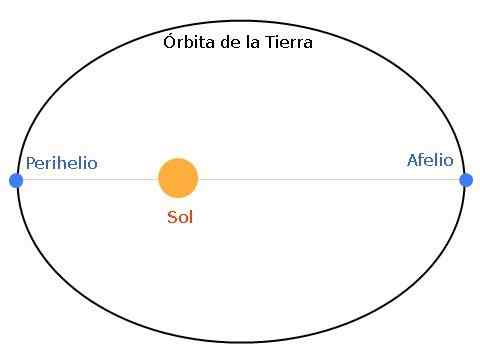Rysunek 1. Orbita Ziemi jest eliptyczna, z słońcem w jednym z ognisk. Kiedy ziemia i słońce znajdują się w maksymalnej odległości, mówi się, że ziemia jest w apheli. A jeśli odległość jest minimalna, mówimy o Perihelio.

Apelium jest najdalszą pozycją od Ziemi do Słońca, podczas gdy peryhelium jest najbliższym punktem. Elipsa może być mniej lub bardziej spłaszczona, zgodnie z charakterystyką systemu gwiazd - planety.

Wartości ASELS i Perihelio różnią się rocznie, ponieważ inne planety powodują zakłócenia. W przypadku innych planet stanowiska te są odpowiednio nazywane wsparciem i wiedzą specjalistyczną.

Wielkość prędkości liniowej planety nie jest stała

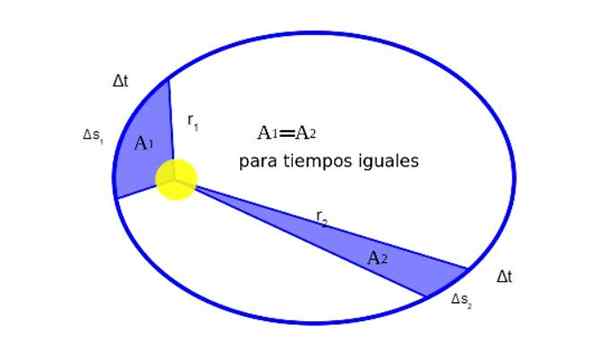
Kepler odkrył, że gdy planeta krąży wokół słońca, podczas ruchu baru równe obszary w równych czasach. Rysunek 2 graficznie pokazuje znaczenie tego:

Może ci służyć: jaka jest równowaga cząstki? (Z przykładami)Rysunek 2. Wektor położenia planety w odniesieniu do słońca to r. Kiedy planeta opisuje jego orbitę, przemieszcza łuk elipsy w czasie δt.

Matematycznie fakt, że₁ Być równe₂ Wyraża się tak:

Trasy łukowe są małe, dzięki czemu każdy obszar może zbliżyć się do trójkąta:

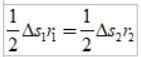
Jako ΔS =vΔT, Gdzie V jest prędkością liniową planety w danym punkcie, podczas wymiany mamy:

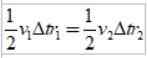
A ponieważ przedział czasowy δT jest taki sam, jest uzyskiwane:

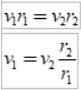
Jak r₂ > r₁, Następnie v₁ > v₂, Innymi słowy, prędkość liniowa planety nie jest stała. W rzeczywistości Ziemia idzie szybciej, gdy znajduje się na peryheliie niż gdy jest w apheli.

Dlatego prędkość liniowa Ziemi lub dowolnej planety wokół Słońca nie jest wielkością, która służy do scharakteryzowania ruchu wspomnianej planety.

Prędkość areolowa

Drugie prawo Keplera sugeruje nową wielkość zwaną prędkością Areolar. Jest zdefiniowany jako obszar zmieciony na jednostkę czasu i jest stały. Aby go obliczyć, używana jest następująca rysunek:

Rysunek 3. Wektor pozycji Ziemi (lub planeta) w odniesieniu do słońca to r, a podczas poruszania się Ziemia doświadcza przemieszczenia, również wektora δR.

Niewielki obszar zmieciony przez Ziemię jest wybierany podczas wykonywania obwodu eliptycznego, który oznaczamy, w jaki sposób δA. Czas potrzebny jest δt.

Rycina 3 pokazuje wektor pozycji Ziemi w odniesieniu do słońca, oznaczony przez r. Kiedy ziemia się porusza, doświadcz przemieszczenia δr.

Obszar ten odpowiada połowy obszaru prostokąta pokazanego na rycinie 3:

Iloraz δR/δT jest dokładnie prędkością liniową Ziemi, więc prędkość areolowa pozostaje:

V_DO W systemie międzynarodowym są:

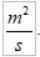
Zauważ, że chociaż zarówno R, jak i V są różne, produkt pozostaje stały. To zamienia prędkość Areolol w bardzo odpowiednią wielkość, aby scharakteryzować ruch planety wokół jej gwiazdy.

Może ci służyć: stałe antoine: wzory, równania, przykłady

Produkt R i V jest wielkością pędu kątowego L, dzięki czemu prędkość areolowa można wyrazić jako:

Obliczanie prędkości liniowej i prędkości Areolar

Z następującym przykładem pokażemy, jak obliczyć prędkość Areol, gdy znane są niektóre parametry ruchu planetarnego:

Ćwiczenia

Zgodnie z prawem Keplera, planeta Exo-Planet porusza się po orbicie eliptycznej. Gdy jest w ekspercie, jego wektor radiowy to r₁ = 4 · 10⁷ km, a kiedy jest na wsparcie, jest r₂ = 15 · 10⁷ km. Prędkość liniowa w swojej wiedzy specjalistycznej to v₁ = 1000 km/s.

Oblicz:

A) Wielkość prędkości w podporach.

B) prędkość areolowa planetu egzo.

C) długość elipsy głównej osi.

Odpowiedz)

Stosuje się równanie:

w którym wymieniane są wartości numeryczne.

Każdy termin jest identyfikowany w następujący sposób:

v₁ = Prędkość wsparcia; v₂ = Prędkość w ekspercie; r₁= Odległość autora,

R₂= Odległość od eksperta.

Przy tych wartościach uzyskuje się:

Odpowiedź b)

Równanie, które należy użyć

w którym można wymienić parę wartości r i v ekspertów lub wspornika, ponieważ v_DO Jest to stała planeta:

Odpowiedź C)

Długość głównej osi elipsy to półsemi -semi -semi -semi -seismum i wiedza specjalistyczna:

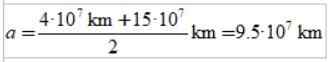
Bibliografia

1. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. Meksyk. Redaktorzy edukacyjni Cengage. 367-372.
2. Stern, d. (2005). Trzy prawa Keplera ruchu planetarnego. Pobrano z PWG.GSFC.garnek.Gov
3. Uwaga: Proponowane ćwiczenie zostało wykonane i zmodyfikowane z następującego tekstu książki McGrawhill. Niestety jest to odosobniony rozdział w formacie PDF, bez tytułu lub autora: MHEDUCATION.ES/BCV/GURL/Rozdział/844817027x.PDF