Definicja wektorów niekoplanowych, warunków, ćwiczeń

Wektory niekoplanarne To ci, którzy nie mają tej samej samolotu. Dwa wolne wektory i jeden punkt definiują pojedynczą płaszczyznę. Trzeci wektor może, ale nie musi, lub nie, a jeśli nie, są to wektory niekoplanowe.

Wektory nieopłatowe nie mogą być reprezentowane w dwóch przestrzeni wymiarowych, takich jak płyta lub arkusz papieru, ponieważ niektóre z nich są zawarte w trzecim wymiarze. Aby ich prawidłowo reprezentować, musisz użyć perspektywy.

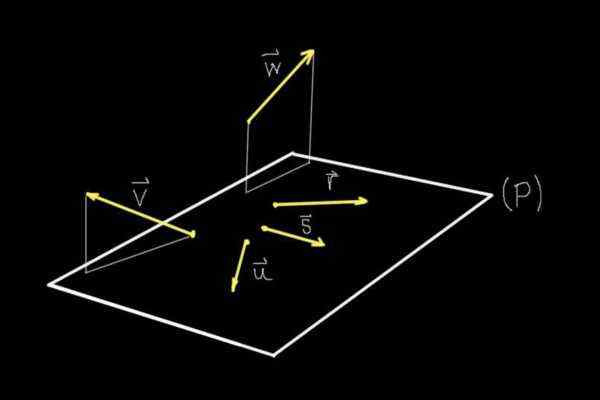Rysunek 1. Coplanares i wektory niezwiązane z. (Własne opracowanie)

Jeśli zaobserwujemy ryc. 1, wszystkie obiekty ściśle pokazane są w płaszczyźnie ekranu, jednak dzięki perspektywie nasz mózg jest w stanie wyobrazić sobie płaszczyznę (P), która wychodzi z tego samego.

Na tej płaszczyźnie (p) są wektory R, S, Lub, podczas gdy wektory v I W  Nie są w tym samolocie.

Dlatego wektory R, S, Lub Są to coplanarios lub coplanares ze sobą, ponieważ mają tę samą samolot (p). Wektory v I W Nie dzielą mieszkań z żadnym z innych pokazanych wektorów, dlatego nie są sprzęgające. 

[TOC]

Wektory coplanares i równania płaski

Płaszczyzna jest jednoznacznie zdefiniowany, czy w przestrzeni trójwymiarowej podano trzy punkty.

Załóżmy, że te trzy punkty są celem DO, punkt B i punkt C które definiują samolot (P). Z tymi punktami można zbudować dwa wektory AB = U I AC = v które są przez konstrukcję z samolotem (P).

Wektor (lub produkt krzyżowy) z tych dwóch wektorów powoduje trzeci wektor prostopadły (lub normalny) do nich, a zatem prostopadle do płaszczyzny (P):

n = u X v   => N ⊥ Lub  I N ⊥ v   => N ⊥ (P)    

Może ci służyć: waga (fizyczna): obliczenia, jednostki, przykłady, ćwiczenia

Każdy inny punkt, który należy do samolotu (P) musi spełnić to wektor Aq być prostopadle do wektora N; Jest to równoznaczne z stwierdzeniem, że produkt skalarny (lub produkt punktowy) N z Aq Musi być zero:

N • • Aq = 0 (*)

Poprzedni warunek jest równoważny, że:

Aq • (Lub X v) = 0 

To równanie zapewnia, że ​​punkt Q należą do samolotu (P). 

Kartezjański równanie samolotu

Poprzednie równanie można napisać w sposób kartezja. W tym celu piszemy współrzędne punktów DO, Q i elementy normalnego wektora N:

A = (A, B, C)

Q = (x, y, z)

N= (NX, NY, NZ)

Tak, aby elementy AQ były:

Aq= (X-A, Y-B, Z-C)

Warunek wektora Aq być zawarte w płaszczyźnie (P) Jest to warunek (*), który jest teraz napisany w ten sposób:

(NX, NY, NZ) • (X-A, Y-B, Z-C) = 0

Obliczanie punktu pozostaje:

NX (X-A) + NY (Y-B) + NZ (Z-B) = 0

Jeśli się rozwinie i zmieni go, pozostanie:

NX X + NY Y + NZ Z = NX A + NY B + NZ C

Poprzednie wyrażenie to równanie kartezjańskie płaszczyzny (P), w zależności od składników normalnego wektora do (P) i współrzędne punktu DO który należy do (P).

Warunki, aby trzy wektory były niekoplanarne

Ponieważ warunek był widoczny w poprzednim rozdziale Aq • (Lub X v) = 0 gwarantuje, że wektor Aq To jest coplanario a Lub I v.

Jeśli zadzwonimy W do wektora Aq Następnie możemy potwierdzić:

W, Lub I v Są koplanaresami, tak i tylko wtedy, gdy W • ( Lub X v ) = 0.

Stan niejednoznaczności

Jeśli produkt potrójnego (lub mieszanego) trzech wektorów różni się od zera, te trzy wektory nie są.

Może ci służyć: proces polityczny: cechy, zastosowania i przykłady

Tak    W • ( Lub X v ) ≠ 0 wówczas wektory u, v i w to nie-kuplanario.

Jeśli kartezjańskie elementy U, V, V i W zostaną wprowadzone, stan nie-zachowania można zapisać w następujący sposób:

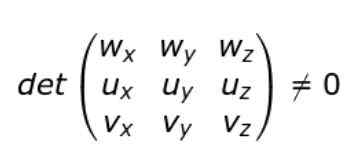To znaczy, że jeśli wyznacznik macierzy (3 × 3), którego wiersze są składnikami wektorów U, V i W, wektory nie są sprzęgające.

Potrójny produkt ma interpretację geometryczną i reprezentuje objętość równoległości generowanych przez trzy wektory innych niż.

Rysunek 2. Trzy wektory nieprzęgające definiują równoległość, którego objętość jest potrójnym modułem produktu. (Własne opracowanie)

Powód tego jest następujący; Gdy dwa wektory nie do sprzętu są mnożone. 

Następnie, gdy ten wektor jest mnożony. 

Innymi słowy, masz powierzchnię równoległoboku wygenerowaną przez pierwsze dwa pomnożone przez wysokość trzeciego wektora.

Alternatywny stan nieprzęgania

Jeśli masz trzy wektory, a żaden z nich nie może być napisany jako liniowa kombinacja pozostałych dwóch, wówczas trzy wektory nie są. To jest trzy wektory Lub, v I W Nie są one, jeśli stan:

α Lub + β v + γ W = 0

Jest to spełnione tylko wtedy, gdy α = 0, β = 0 i γ = 0.

Rozwiązane ćwiczenia

-Ćwiczenie 1

Masz trzy wektory

Lub = (-3, -6, 2);   v = (4, 1, 0) i W = (-1, 2, z)

Zauważ, że komponent Z wektora W Nie wiadomo.

Znajdź zakres wartości, które Z może podjąć, aby gwarantowano, że trzy wektory nie dzielą tej samej płaszczyzny.

Może ci służyć: stabilna równowaga: koncepcja i przykłady

Rozwiązanie 

Ponownie stosujemy kryterium wyznacznika matrycy utworzonej przez szeregi trzech wektorów, w ten sposób pozostajemy: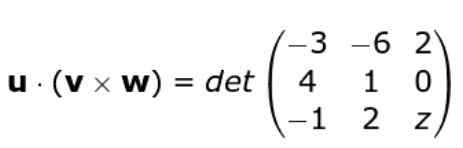Rozwijamy determinant

W • ( Lub X v ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3Z + 24Z + 18 = 21Z + 18

Dopasowujemy to wyrażenie o wartości zerowej

21 Z + 18 = 0

I oczyścimy Z

Z = -18/21 = -6/7

Jeśli zmienna Z wzięła wartość -6/7, trzy wektory byłyby koplanares.

Tak, że wartości Z, które gwarantują, że wektory są nie-ożywcami, to te, które są w następującym odstępie:

Z ∈ (-∞, -6/7) u (-6/7, ∞)

-Ćwiczenie 2

Znajdź objętość równoległości pokazanej na poniższym rysunku:

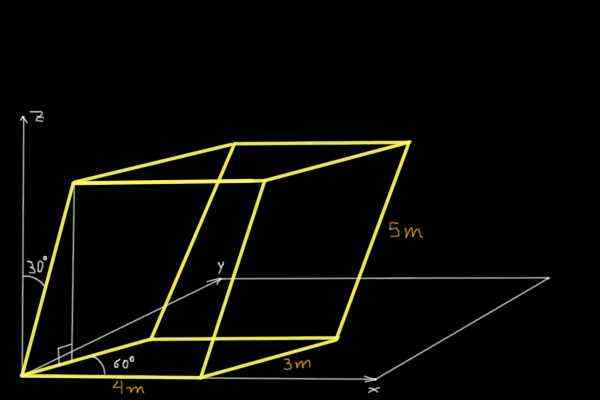
Rozwiązanie 

Aby znaleźć objętość równoległości pokazanej na rysunku, komponenty kartezjańskie trzech niekontrolowanych wektorów nieprzężących zostaną określone w pochodzeniu układu współrzędnych. Pierwszy to wektor Lub  4M i równolegle do osi x:

Lub= (4, 0, 0) m

Drugi to wektor v W płaszczyźnie rozmiaru XY 3M, która tworzy 60º z osą x:

v= (3*cos 60º, 3*Sen 60º, 0) = (1.5, 2.6, 0.0) m

I trzeci wektor W 5m i którego projekcja w płaszczyźnie XY tworzy 60º z osą x, dodatkowo W tworzy 30º.

W= (5*sin 30º*cos 60º, 5*Sen 30º*sin 60º, 5*Sen 30º)

Przeprowadziliśmy obliczenia, które mamy: W= (1.25, 2.17, 2.5m.

Bibliografia

1. Figueroa, zm. Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. 31-68.
2. Fizyczny. Moduł 8: wektory. Odzyskane z: frtl.Utn.Edu.ar
3. Hibbeler, R. 2006. Mechanika inżynierów. Statyczny. 6. edycja. Continental Editorial Company.28-66.
4. McLean, w. Seria Schaum. Mechanika inżynierów: statyczne i dynamiczne. Wydanie trzecie. McGraw Hill. 1-15.
5. Wikipedia. Wektor. Odzyskane: to jest.Wikipedia.org