Względna koncepcja prędkości, przykłady, ćwiczenia

Względna prędkość obiektu jest mierzony w odniesieniu do danego obserwatora, ponieważ inny obserwator może uzyskać inną miarę. Prędkość zawsze zależy od obserwatora, który ją mierzy.

Dlatego prędkość obiektu mierzona przez określoną osobę będzie względna prędkość w stosunku do niej. Inny obserwator może uzyskać inną wartość dla prędkości, wciąż w przypadku tego samego obiektu.

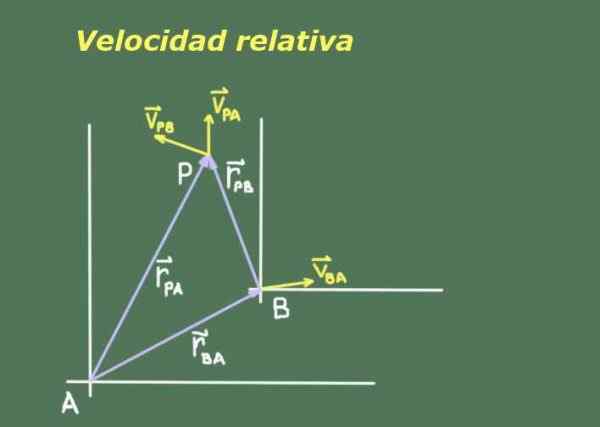
Rysunek 1. Schemat reprezentujący punkt P w ruchu, widoczny z systemów referencyjnych A i B. Źródło: Self Made.

Jak dwóch obserwatorów a i b, którzy poruszają się od siebie, mogą mieć różne miary trzeciego obiektu P, który się porusza, konieczne jest poszukiwanie związku między pozycjami i prędkością widoków P przez A i B.

Rycina 1 pokazuje dwóch obserwatorów A i B z odpowiednimi systemami odniesienia, z których mierzą położenie i prędkość obiektu P.

Każdy obserwator A i B mierzy pozycję i prędkość obiektu P o określonym czasie T. W klasycznej względności (lub Galilean) czas dla obserwatora A jest taki sam jak dla obserwatora B, niezależnie od jego względnych prędkości.

Ten artykuł dotyczy klasycznej względności, która jest ważna i ma zastosowanie do większości codziennych sytuacji, w których obiekty mają znacznie niższe prędkości niż światło.

Pozycja obserwatora B dotycząca oznaczeń jako R_BA. Ponieważ pozycja jest kwotą wektorową, używamy Bold, aby ją wskazać. Pozycja obiektu p w odniesieniu do A oznacza jako R_Rocznie i ten sam obiekt P w odniesieniu do B R_Pb.

[TOC]

Związek między pozycjami a prędkościami względnymi

Istnieje związek wektorowy między tymi trzema pozycjami, które można wywnioskować z reprezentacji ryc. 1:

 R_Rocznie= R_Pb + R_BA

Jeśli poprzednie wyrażenie jest przyjmowane w odniesieniu do czasu T Uzyskamy związek między względnymi prędkościami każdego obserwatora:

Możesz Ci służyć: drugie prawo Newtona: aplikacje, eksperymenty i ćwiczenia

V_Rocznie= V_Pb + V_BA

W poprzednim wyrażeniu istnieje względna prędkość p w odniesieniu do A w zależności od względnej prędkości p w odniesieniu do B i względnej prędkości B w odniesieniu do.

Podobnie względna prędkość P można zapisać w odniesieniu do względnej prędkości p w odniesieniu do A i względnej prędkości B.

V_Pb= V_Rocznie + V_Ab

Należy zauważyć, że względna prędkość B w odniesieniu do B jest równa i sprzeczna z prędkością B w odniesieniu do A:

V_Ab = -V_BA 

Widać to przez dziecko z poruszającego się samochodu

Samochód idzie prostą drogą, która przechodzi z zachodu do tego, szybko z 80 km/h, podczas gdy w przeciwnym kierunku (a na drugim pasie) pojawia się motocykl szybko 100 km/h.

Na tylnym siedzeniu samochodu podróżuje dziecko, które chce poznać względną prędkość motocykla, który do niego zbliża się. Aby znaleźć odpowiedź, dziecko zastosuje relacje, które właśnie przeczytałeś w poprzedniej sekcji, identyfikując każdy układ współrzędnych w następujący sposób:

-A jest układem współrzędnych obserwatora na drodze i w odniesieniu do niego, mierzono rapidy każdego pojazdu.

-B to samochód, a P będzie motocyklem.

Jeśli chcesz obliczyć prędkość moto p w odniesieniu do samochodu B, zastosowano następującą zależność:

V_Pb= V_Rocznie + V_Ab=V_Rocznie - V_BA

Przyjmując jako pozytywny kierunek na zachód-wschód:

V_Pb= (-100 km/h - 80 km/h) Siema = -180 km/h Siema

Wynik ten jest interpretowany w następujący sposób: motocykl porusza się w odniesieniu do samochodu z prędkością 180 km/h i kierunkiem -Siema, to znaczy West.

Może ci służyć: Algebra Block: Elementy, przykłady, rozwiązane ćwiczenia

Względna prędkość między motocyklem a samochodem

Motocykl i samochód przekroczyły każdy po ich linii. Chłopiec, który idzie na tylnym siedzeniu samochodu, widzi motocykl i teraz chce wiedzieć, jaką prędkość odsuwa się od niego, zakładając, że zarówno motocykl, jak i samochód utrzymują takie same rapides, co przed przejściem.

Aby poznać odpowiedź, dziecko stosuje ten sam związek, który był wcześniej używany:

V_Pb= V_Rocznie + V_Ab=V _Rocznie - V_BA

V_Pb= -100 km/h Siema - 80 km/h Siema = -180 km/h Siema

A teraz motocykl odsuwa się od samochodu z tą samą względną prędkością, z jaką zbliżyli się przed skrzyżowaniem.

Ten sam motocykl z części 2 powraca, zachowując swoją samą prędkość 100 km/h, ale zmieniając swój adres. To znaczy samochód (który kontynuuje szybko 80 km/h), a motocykl porusza się w pozytywnym kierunku.

W pewnym momencie motocykl przekroczy samochód, a dziecko, które idzie na tylnej siedzeniu samochodu, chce poznać względną prędkość motocykla w odniesieniu do niego.

Aby uzyskać odpowiedź, dziecko ponownie stosuje relacje ruchu względnego:

V_Pb= V_Rocznie + V_Ab=V_Rocznie - V_BA

V_Pb= +100 km/h Siema - 80 km/h Siema = 20 km/h Siema 

Dziecko z tylnego siedzenia obserwuje motocykl rozwijający samochód z prędkością 20 km/h.

-Ćwiczenie rozwiązane

Ćwiczenie 1

Łódź motorowa przecina rzekę o szerokości 600 m i płynie z północy na południe. Prędkość rzeki wynosi 3 m/s. Prędkość łodzi w odniesieniu do wody rzecznej wynosi 4 m/s na wschodzie.

Może ci służyć: gałęzie klasycznej i nowoczesnej fizyki

(i) Znajdź prędkość łodzi w odniesieniu do brzegu rzeki.

(ii) Wskaż prędkość i kierunek łodzi w odniesieniu do lądu.

(iii) Oblicz czas przejścia.

(iv) ile przeniosło się na południe w odniesieniu do punktu początkowego.

Rozwiązanie 

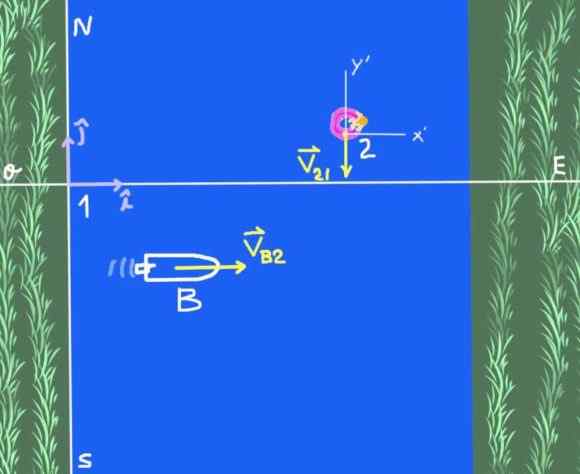Rysunek 2. Łódź przekraczająca rzekę (Ćwiczenie 1). Źródło: Self Made.

Istnieją dwa systemy odniesienia: system referencyjny solidarności na brzegu rzeki, który wywołamy 1 i system referencyjny 2, który jest obserwatorem, który unosi się na wodzie rzeki. Celem studiów jest łódź b.

Prędkość łodzi w odniesieniu do rzeki jest zapisana w formie wektorowej w następujący sposób:

VB2 = 4 Siema SM

Prędkość obserwatora 2 (tratwa nad rzeką) w odniesieniu do obserwatora 1 (na lądzie):

Vdwadzieścia jeden = -3 J SM

Chcesz znaleźć prędkość łodzi w odniesieniu do ziemi VB1.

VB1 = VB2 + Vdwadzieścia jeden

Odpowiedz i

VB1 = (4 Siema - 3 J) SM   

Prędkość łodzi będzie poprzednim modułem prędkości:

|VB1|. = (42 + (-3) 2) ½ = 5 m/s

Odpowiedź ii

A adres będzie:

θ = arcan (-¾) = -36,87º 

Odpowiedź iii

Czas przekraczania łodzi to stosunek między szerokością rzeki a komponentem X prędkości łodzi w odniesieniu do Ziemi.

t = (600 m)/(4 m/s) = 150 s 

Odpowiedź iv

Aby obliczyć dryf, który łódź miała na południu, komponent i prędkość łodzi w odniesieniu do ziemi są mnożone przez czas przejścia:

D = -3 J m/s * 150 s = -450 J M

Przemieszczenie na południe w odniesieniu do punktu początkowego wynosi 450 m.

Bibliografia

1. Giancoli, zm. Fizyka. Zasady z aplikacjami. 6. edycja. Prentice Hall. 80-90
2. Resnick, r. (1999). Fizyczny. Tom 1. Trzecie wydanie po hiszpańsku. Meksyk. Continental Editorial Company S.DO. c.V. 100-120.
3. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wydanie. Meksyk. Redaktorzy edukacyjni Cengage. 95-100.
4. Wikipedia. Względna prędkość. Odzyskane z: Wikipedia.com
5. Wikipedia. Metoda względnej prędkości. Odzyskane z: Wikipedia.com