Bezpłatne właściwości wektorów, przykłady, ćwiczenia

Darmowe wektory Są tymi, które są w pełni określone przez ich wielkość, ich kierunek i znaczenie, bez konieczności wskazania punktu zastosowania lub określonego pochodzenia.

Ponieważ w ten sposób można narysować nieskończone wektory, wolny wektor nie jest unikalnym bytem, ​​ale zestawem wektorów równoległych i identycznych, które są niezależne od miejsca, w którym się znajdują.

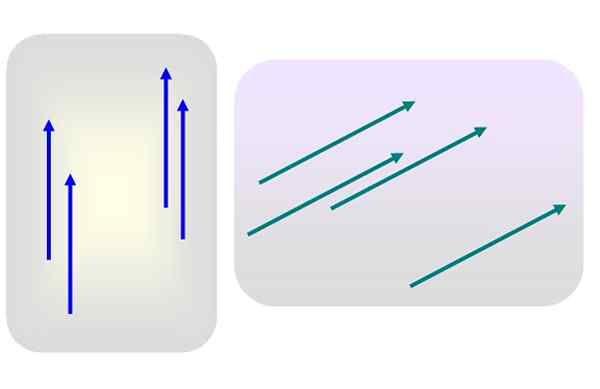
Rysunek 1. Różne bezpłatne wektory. Źródło: Self Made.

Powiedzmy, że istnieje kilka wektorów wielkości 3 ukierunkowanych pionowo, lub wielkości 5 i skłonnych do prawej, jak na rycinie 1.

Żaden z tych wektorów nie jest specjalnie stosowany. Wówczas którykolwiek z niebieskich lub zielonych wektorów jest reprezentatywny dla ich odpowiedniej grupy, ponieważ jej charakterystyka - moduł, kierunek i sens - wcale nie są modyfikowane, gdy są one przeniesione do innego miejsca płaszczyzny.

Bezpłatny wektor jest zwykle oznaczony w tekście drukowanym z małą i odważną literą, na przykład v. Lub z małymi literami i strzałką na górze, jeśli jest to tekst rękopisu.

[TOC]

 Przykłady

Zaletą, jaką mają wolne wektory, jest to, że można je przenosić samolotem lub przestrzenią i zachować swoje właściwości, ponieważ każdy przedstawiciel zestawu jest równie ważny.

Dlatego w fizyce i mechanice są często używane. Na przykład, aby wskazać prędkość liniową stałego, która porusza się, nie jest konieczne wybór konkretnego punktu obiektu. Następnie wektor prędkości zachowuje się jak wolny wektor.

Innym przykładem wolnego wektora jest para sił. A para Składa się z dwóch sił o równej wielkości i kierunku, ale przeciwnych zmysłów, stosowanych w różnych punktach stałego. Efektem pary nie jest przenoszenie obiektu, ale spowodowanie obrotu dzięki za chwilę wytworzony.

Rysunek 2 pokazuje parę sił nakładanych na kierownicę. Poprzez siły F₁ I F₂, Moment obrotowy obracający kierownicę wokół jej środka jest tworzony i w harmonogramie.

Może ci służyć: azotek boru (BN): Struktura, właściwości, uzyskiwanie, użycia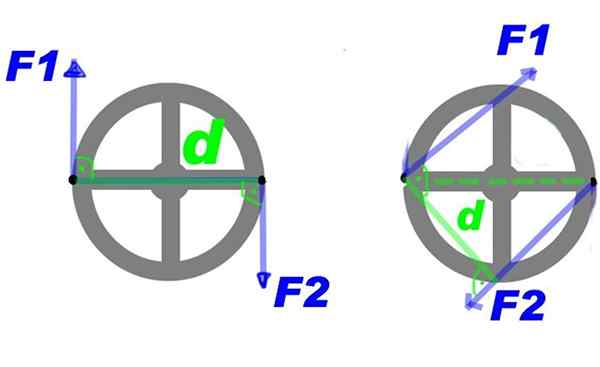 Rysunek 2. Kilka sił nakładanych na kierownicę zapewnia zwrot punktowy. Źródło: Benko [domena publiczna].

Możesz wprowadzić pewne zmiany w parze i nadal uzyskać ten sam efekt obrotowy, na przykład zwiększyć siłę, ale zmniejszyć odległość między nimi. Lub zachowaj siłę i odległość, ale nałóż parę na kolejne kilka punktów na kierownicy, to znaczy obróć moment obrotowy wokół środka.

Czas pary sił lub po prostu para, Jest to wektor, którego moduł jest FD i jest prostopadle do płaszczyzny koła prostopadle. W przykładzie pokazanym przez konwencję zwrot czasu ma negatywny sens.

Właściwości i cechy

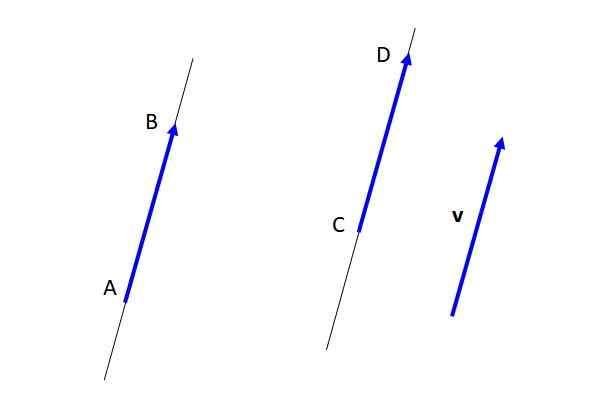
W przeciwieństwie do wolnego wektora V, wektory Ab I płyta CD Są naprawione (patrz rysunek 3), ponieważ określały punkt początkowy i punkt przybycia. Ale bycie ze sobą, a z kolei z wektorem v, Są reprezentatywne dla wolnego wektora v.

Rysunek 3. Darmowe wektory, sprzęt i stałe wektory. Źródło: Self Made.

Główne właściwości wolnych wektorów są następujące:

-Dowolny wektor Ab (Patrz rysunek 2), jak wspomniano, jest reprezentatywnym dla wolnego wektora v.

-Moduł, kierunek i znaczenie są takie same w każdym przedstawiciela wolnego wektora. Na rycinie 2 wektory Ab I płyta CD Reprezentują bezpłatny wektor v I są to sprzęt.

-Biorąc pod uwagę punkt P miejsca, zawsze można znaleźć przedstawiciela wolnego wektora v którego pochodzenie jest w P i Said Representatent jest wyjątkowy. To najważniejsza właściwość wolnych wektorów i ta, która czyni je tak wszechstronnymi.

Może ci służyć: Europa (satelita): cechy, skład, orbita, ruch

-Voyed Wolny wektor jest oznaczony jako 0 I jest to zestaw wszystkich wektorów, które nie mają wielkości, kierunku i znaczenia.

-Jeśli wektor Ab reprezentuje wolny wektor v, Następnie wektor BA reprezentuje wolny wektor -v.

-Notacja zostanie użyta V³ Aby wyznaczyć zestaw wszystkich wektorów pozbawionych przestrzeni i V² Aby wyznaczyć wszystkie bezpłatne wektory samolotu.

Rozwiązane ćwiczenia

Dzięki bezpłatnym wektorom możesz wykonać następujące operacje:

-Dodatek

-Odejmowanie

-Mnożenie wspinaczki przez wektor

-Produkt skalarny między dwoma wektorami.

-Produkt między dwoma wektorami

-Liniowa kombinacja wektorów

I więcej.

-Ćwiczenie 1

Uczeń zamierza pływać z punktu na brzegu z jednej rzeki do drugiej, która jest dokładnie z przodu. Aby nie osiągnąć niczego bezpośrednio z prędkością 6 km / h, w kierunku prostopadłym, jednak prąd ma prędkość 4 km / h, która go kieruje.

Oblicz prędkość wynikającą z pływaka i ile kieruje się przez prąd.

Rozwiązanie

Rozszerzająca prędkość pływaka jest sumą wektorową jego prędkości (w odniesieniu do rzeki, narysowanej pionowo) i prędkością rzeki (narysowanej od lewej do prawej), która jest przeprowadzana, jak wskazano na poniższym rysunku:

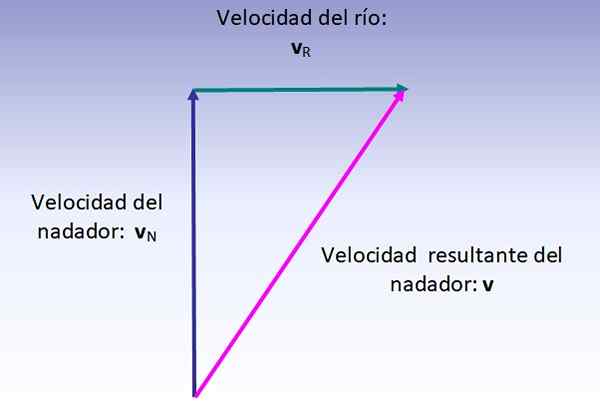
Wielkość powstałej prędkości odpowiada przedpotenu pokazanego prawego trójkąta, zatem:

V = (6² + 4²) ^½ km/h = 7.2 km/h

Adres można obliczyć według kąta w odniesieniu do prostopadłego do brzegu:

α = ARCTG (4/6) = 33.7 lub 56.3. o brzegu.

Ćwiczenie 2

Znajdź czas pary sił pokazanych na rysunku:

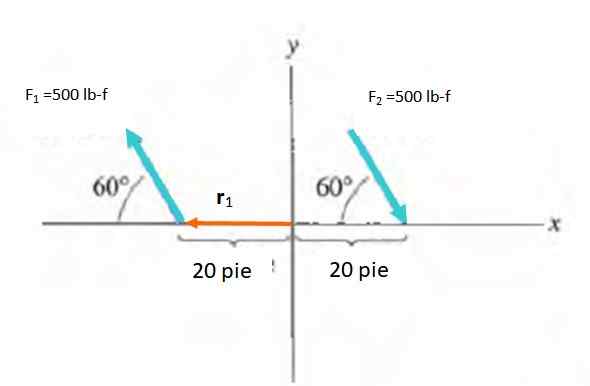
Rozwiązanie

Moment jest obliczany przez:

Może ci służyć: wstrząsy nieelastyczne: w wymiarze i przykładach

M = R X F

Jednostki chwili to LB-F.stopa. Ponieważ moment obrotowy znajduje się w płaszczyźnie ekranu, moment jest skierowany prostopadle do niego, na zewnątrz lub do wewnątrz.

Ponieważ moment obrotowy przykładu ma tendencję do włączania obiektu, na który jest stosowany (który nie jest pokazany na rysunku) w harmonogramie, ten moment jest rozważany przez wskazanie wewnątrz ekranu i z znakiem ujemnym.

Wielkość momentu to m = f.D.sin a, będąc pod kątem między siłą a wektorem R. Musisz wybrać punkt, dla którego można obliczyć moment, który jest wolnym wektorem. Dlatego pochodzenie systemu odniesienia R przechodzi od O do punktu zastosowania każdej siły.

M₁ = M₂ = -FDSEN60º = -500 . 20 .Sen 60º lb-f . stopa = -8660.3 funty-f . stopa

Moment netto jest sumą m₁ oraz m₂: -17329.5 lb-f . stopa.

Bibliografia

1. Beardon, t. 2011. Wprowadzenie do wektorów. Odzyskany z: nrich.Matematyka.org.
2. Bedford, 2000. DO. Mechanika inżynierii: statyczne. Addison Wesley. 38-52.
3. Figueroa, zm. Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka.31-68.
4. Fizyczny. Moduł 8: wektory. Odzyskane z: frtl.Utn.Edu.ar
5. Hibbeler, R. 2006. Mechanika inżynierów. Statyczny. 6. edycja. Continental Editorial Company. 15-53.
6. Wektor kalkulatora dodania. Odzyskane z: 1728.org
7. Wektory. Odzyskane: to jest.Wikibooks.org