Wynikowe obliczenia wektora, przykłady, ćwiczenia

On wynikowy wektor Jest to ta uzyskana przez operację z wektorami, których wynik jest również wektorem. Zwykle operacja ta jest sumą dwóch lub więcej wektorów, za pomocą której uzyskuje się wektor, którego efekt jest równoważny.

W ten sposób uzyskane są wektory, takie jak prędkość, przyspieszenie lub siła. Na przykład, gdy kilka sił działa na ciało F₁, F₂, F₃,.. . Suma wektorowa wszystkich tych sił jest równoważna sile netto (wynikowa), która matematycznie wyraża się:

F₁ + F₂ + F₃ +… = F_R  albo F_N

Rysunek 1. Waga śniegu jest rozłożona na suficie, a jego działanie można zastąpić pojedynczą wynikową siłą przyłożoną w odpowiednim miejscu. Źródło: Pixabay.

Powstały wektor, niezależnie od tego, czy jest to siły, czy jakakolwiek inna wielkość wektora, stosuje zasady sumy wektorów. Ponieważ wektory mają kierunek i sens oprócz wartości numerycznej, nie wystarczy dodać moduły, aby mieć wynikowy wektor.

Jest to prawdą tylko w przypadku, w którym zaangażowane wektory są w tym samym kierunku (patrz przykłady). W przeciwnym razie konieczne jest użycie metod sum wektorowych, które w zależności od przypadku mogą być geometryczne lub analityczne.

[TOC]

Przykłady

Metody geometryczne w celu znalezienia powstałego wektora to metoda wielokąta i metoda równoległoboku.

Jeśli chodzi o metody analityczne, jest metodą składową, za pomocą której można znaleźć wektor wynikający z dowolnego systemu wektorowego, o ile mamy jego komponenty kartezjańskie.

Metody geometryczne do dodania dwóch wektorów

Załóżmy, że wektory Lub I v (Oznaczamy je odważne, aby odróżnić je od skalarnego). Na rycinie 2) mamy je zlokalizowane w samolocie. Na ryc. 2 B) przeniósł się do wektora V w taki sposób, że jego pochodzenie zbiega się z końcem Lub. Powstały wektor wychodzi z pochodzenia pierwszego (Lub) na wierzchołek ostatniego (v):

Może ci służyć: ściśliwość: stałe, ciecze, gazy, przykłady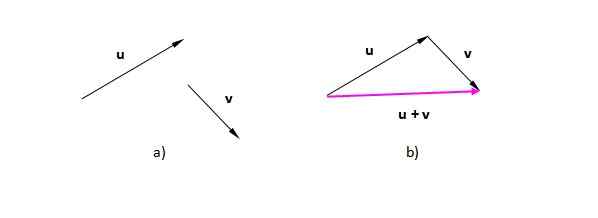 Rysunek 2. Powstały wektor z graficznej sumie wektorów. Źródło: Self Made.

Rysunek, który w tym przypadku powstaje w tym przypadku (trójkąt to trójkąt 3). Jeśli mamy dwa wektory w tym samym kierunku, procedura jest taka sama: umieść jeden z wektorów po drugiej i narysuj jeden, który przechodzi od pochodzenia lub ogona pierwszego do końcówki lub końca ostatniego.

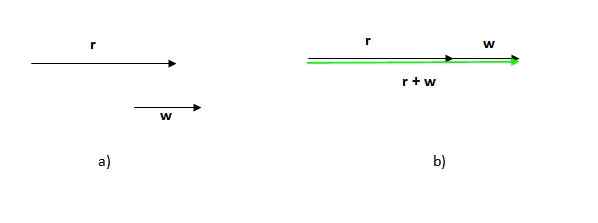
Zwróć uwagę, że kolejność dokonywanej tej procedury nie ma znaczenia, ponieważ suma wektorów jest zgodna.

Zauważ też, że w tym przypadku moduł (Długość lub rozmiar) powstałego wektora jest sumą modułów dodatkowych wektorów, w przeciwieństwie do poprzedniego przypadku, w którym wynikowy moduł wektorowy jest mniejszy niż suma modułów uczestników.

Metoda równoległobramowa

Ta metoda jest bardzo odpowiednia, gdy trzeba dodać dwa wektory, których punkty pochodzenia się zgadzają, z pochodzeniem układu współrzędnych x-y. Załóżmy, że tak jest w przypadku naszych wektorów Lub I v (Rysunek 3):

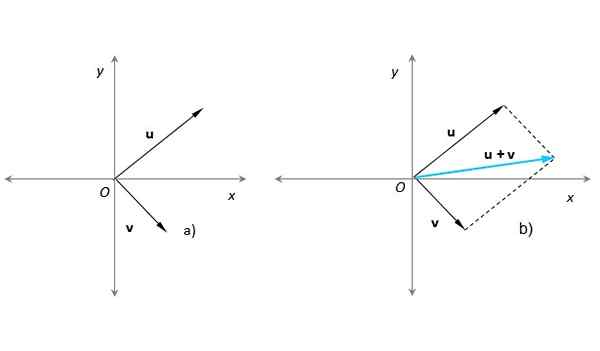Rysunek 3. Suma dwóch wektorów za pomocą metody równoległoboku z wynikowym wektorem w turkusowym niebieskim niebieskim. Źródło: Self Made.

Na rycinie 3b) zbudowano równoległobok z pomocą równoległych kropkowanych linii do Lub już v. Powstały wektor ma swoje pochodzenie w O i jego koniec w punkcie, w którym przecinają się kropkowane linie. Ta procedura jest całkowicie równoważna tej opisanej w poprzednim rozdziale.

Ćwiczenia

-Ćwiczenie 1

Biorąc pod uwagę następujące wektory, znajdź wynikowy wektor przy użyciu metody wielokąta.

Może ci służyć: odbicie światła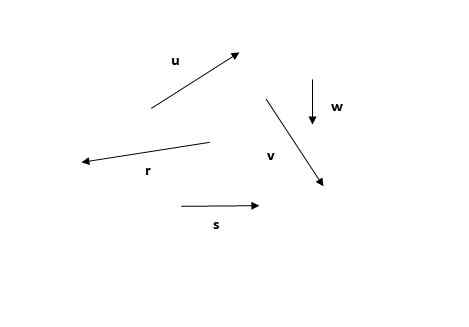 Rysunek 4. Wektory, które można znaleźć w wyniku metody wielokąta. Ćwiczenie 1. Źródło: Self Made.

Rozwiązanie

Metoda wielokątna jest pierwszą z widzianych metod. Pamiętaj, że suma wektorów jest przemienna (kolejność dodatków nie zmienia sumy), więc na przykład możesz zacząć od dowolnego wektorów Lub (Rysunek 5a) lub R (Rysunek 5b):

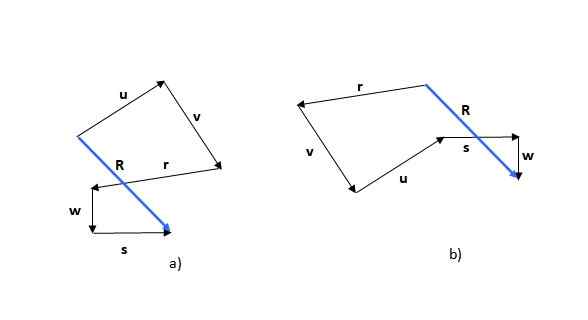Rysunek 5. Suma wektorów metodą wielokątną. Źródło: Self Made.

Uzyskana liczba to wielokąt, a powstały wektor (na niebiesko) jest wywoływany R. Jeśli zaczniesz od innego wektora, utworzona liczba może być inna, jak widać w przykładzie, ale wynikowy wektor jest taki sam.

Ćwiczenie 2

Na poniższym rysunku wiadomo, że moduły wektorów Lub I v odpowiednio to u = 3 arbitralne jednostki i v = 1.8 jednostek arbitralnych. Kąt to Lub forma z dodatnią osą x wynosi 45 ° v uformuje 60 ° z osi y, jak widać na rysunku. Znajdź wynikowy wektor, wielkość i kierunek.

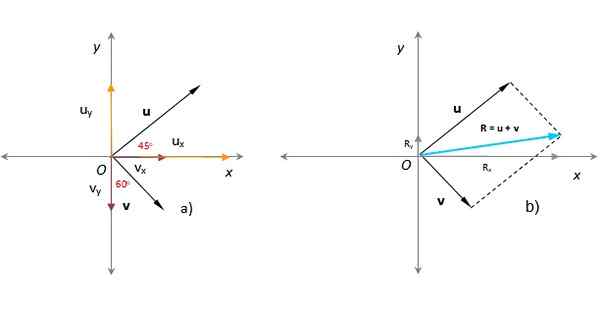
Rozwiązanie

W poprzednim rozdziale stwierdzono, że powstały wektor stosuje metodę równoległoboku (w turkusowym na rysunku).

Prostym sposobem na analizę uzyskanego wektora jest wyrażanie wektorów dodających pod względem ich komponentów kartezjańskich, co jest łatwym zadaniem, gdy znany są moduł i kąt, takie jak wektory tego przykładu:

Lub_X = u . cos 45º = 3 x cos 45 º = 2.12; Lub_I = u . Sin 45 º = 3x Sen 45º = 2.12

v_X = v . Sen 60º = 1.8 x Sen 60 º = 1.56; v_I = -V . cos 60 º = -1.8 x cos 60º = - 0.9

Może ci służyć: ruch wahadłowy

Wektory Lub I v Są wektorami należącymi do samolotu, mają dwa dwa elementy każdy. Wektor U znajduje się w pierwszej ćwiartce, a jego składniki są dodatnie, podczas gdy wektor V znajduje się w czwartym kwadrancie; Jego element x jest dodatni, ale jego rzut na osi pionowej wpada w osą i ujemną.

Obliczanie komponentów kartezjańskich powstałego wektora

Powstały wektor dodaje algebraicznie odpowiednie komponenty X i Y, aby uzyskać jego komponenty kartezjańskie:

R_X = 2.12 + 1.56 = 3.68

R_I = 2.12 + (-0.9) = 1.22

Po określaniu komponentów kartezjańskich i wektor jest całkowicie znany. Powstały wektor można wyrazić notację w nawiasach kwadratowych (wsporniki):

R = jednostki arbitralne

Notacja wspornika służy do odróżnienia wektora od punktu w płaszczyźnie (lub w przestrzeni). Innym sposobem wyrażania uzyskanego wektora w sposób analityczny jest użycie wektorów jednostkowych Siema i J w samolocie (Siema, J I k w kosmosie):

R = 3.68 Siema + 1.22 J jednostki arbitralne

Ponieważ oba elementy powstałego wektora są dodatnie, wektor R Należy do pierwszej ćwiartki, która była już widoczna graficznie.

Wielkość i kierunek powstałego wektora

Znana z komponentów kartezjańskich, wielkość R jest obliczana przez twierdzenie Pitagorasa, ponieważ powstały wektor R, obok jego komponentów r_X i r_I Tworzą prawy trójkąt:

Wielkość lub moduł: r = (3.68² + 1.22²)^½ = 3.88

Adres q przyjmujący dodatnią osi x jako odniesienie: q = arcan (r_I / R_X) = arctg (1.22/3.68) = 18.3

Bibliografia

1. Dodawanie wektorów i zasad. Odzyskane z: Newt.Phys.UNSW.Edu.Au
2. Figueroa, zm. Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka.31-68.
3. Fizyczny. Moduł 8: wektory. Odzyskane z: frtl.Utn.Edu.ar
4. Hibbeler, R. 2006. Mechanika inżynierów. Statyczny. 6. edycja. Continental Editorial Company. 15-53.
5. Wektor kalkulatora dodania. Odzyskane z: www.1728.org