Fizyczny

Definicja wektorów Equidocent, notacja, ćwiczenia

Definicja wektorów Equidocent, notacja, ćwiczenia

Dwa lub więcej Wektory to sprzęt Jeśli mają ten sam moduł, ten sam kierunek i równy sens, nawet gdy ich punkt pochodzenia jest inny. Pamiętaj, że cechy wektora są dokładnie: pochodzenie, moduł, kierunek i sens. 

Wektory są reprezentowane przez segment zorientowany lub strzałki. Ryc. 1 pokazuje reprezentację kilku wektorów w płaszczyźnie, z których niektóre są sprzętem zgodnie z początkowo podaną definicją.

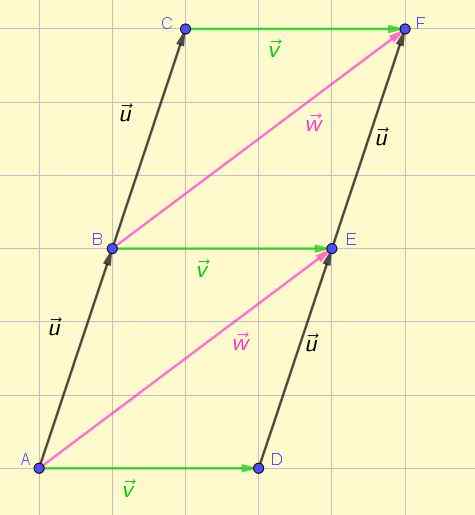Rysunek 1. Wektory sprzętu i nierównomierności. Źródło: Self Made.

Od pierwszego spojrzenia można docenić, że trzy zielone wektory mają ten sam rozmiar, ten sam kierunek i ten sam sens. To samo można potwierdzić o dwóch różowych wektorach i czterech czarnych wektorach.

Liczne wielkości natury mają zachowanie wektorowe, taka jest przypadek prędkości, przyspieszenia i siły, aby wymienić tylko niektóre. Stąd znaczenie właściwie ich scharakteryzowania.

[TOC]

Notacja dla wektorów i sprzętu

Aby rozróżnić kwoty wektorowe kwot skalarnych, często używana jest litera typu czarnego lub strzałka na literę. Podczas pracy z wektorami ręcznymi, na notebookie, konieczne jest rozróżnienie ich za pomocą strzałki, a gdy używane jest wydrukowane medium, używane są odważne.

Wektory można odmówić wskazującego ich punkt początkowy lub pochodzenie i punkt przybycia. Na przykład Ab, pne, Z I Ef na rycinie 1 są jednak wektory Ab, pne, Z I Ef Są to wielkości skalarne lub liczby wskazujące wielkość, moduł lub wielkość ich odpowiednich wektorów.

Aby wskazać, że dwa wektory to sprzęt, używany jest symbol ”∼ ”. Dzięki tej notacji na rysunku możemy wskazać następujące wektory, które są ze sobą sprzętu:

Może ci służyć: energia kinetyczna: cechy, typy, przykłady, ćwiczenia

Ab∼BC∼De  

Wszystkie mają tę samą wielkość, kierunek i znaczenie. Dlatego spełnia się z wyżej wymienionych przepisów.

Wektory wolne, przesuwane i przeciwne

Każdy z wektorów na rysunku (na przykład Ab) jest przedstawicielem zbioru wszystkich stałych wektorów. Ten nieskończony zestaw określa klasę wolnych wektorów Lub.

Lub = AB, BC, z, ef, ..

Alternatywna notacja jest następująca:

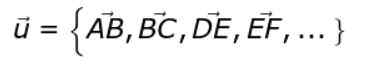
Jeśli odważna lub strzałka nie jest umieszczona na górze Lub, Chcemy odwołać się do modułu wektorowego Lub.

Darmowe wektory nie są stosowane do jakiegoś konkretnego punktu.

Z ich strony Przesuwane wektory Są to sprzęt do danego wektora, ale ich punkt zastosowania musi być zawarty w linii akcji wektorowej.

I przeciwne wektory Są to wektory, które mają tę samą wielkość i kierunek, ale przeciwne zmysły, chociaż w angielskich tekstach są nazywane przeciwne adresy Ponieważ adres wskazuje również znaczenie. Przeciwne wektory nie są wyposażeniem.

Ćwiczenia

-Ćwiczenie 1

Które inne wektory pokazane na rycinie 1 są ze sobą sprzętu?

Rozwiązanie

Oprócz tych już wskazanych w poprzednim rozdziale, obserwuje się to na rycinie 1 OGŁOSZENIE, Być I Ec Są również wektorami równoważnymi ze sobą:

AD ∼ BE ∼ CE 

Każdy z nich jest przedstawicielem klasy wolnych wektorów v.

Wektory są również między sobą sprzętu Ae I Bf :

Ae ∼ Bf 

Którzy są przedstawicielami klas W.

-Ćwiczenie 2

Punkty A, B i C są na kartezyjskim płaszczyźnie XY, a ich współrzędne to:

Może ci służyć: idealny gaz: model, zachowanie, przykłady

A = (-4,1), b = (-1,4) i c = (-4, -3)

Znajdź współrzędne czwartego punktu D, aby wektory Ab I płyta CD Być wyposażeniem.

Rozwiązanie 

Aby płyta CD być wyposażeniem Ab Musi mieć ten sam moduł i ten sam kierunek co Ab .

Moduł Ab Square to:

|Ab|^2 = (-1 -( -4))^2 + (4-1)^2 = 9 + 9 = 18

D Współrzędne są nieznane z tego, co możemy powiedzieć: D = (x, y)

Następnie: |płyta CD|^2 = (x -(-4))^2 + (y -( -3))^2

As |Ab| = |płyta CD|. Jest to jeden z warunków Ab I płyta CD Być wyposażeniem:

(x + 4)^2 + (y + 3)^2 = 18

Ponieważ istnieją dwa niewiadome, wymagane jest inne równanie, które można osiągnąć w stanie Ab I płyta CD Bądź równolegle i w tym samym sensie.

Wektor AB Slope

Nachylenie wektora Ab Wskazuje twój adres:

Oczekujący AB = (4-1)/(-1 -( -4)) = 3/3 = 1

Wskazując, że wektor Ab 45º forma z osą x.

Nachylenie wektora CD

Stok płyta CD Oblicza się podobnie:

Oczekujący CD = (y -( -3))/(x -(-4)) = (y + 3)/(x + 4)

Dopasowanie tego wyniku do nachylenia Ab Masz następujące równanie:

Y + 3 = x + 4 

Co oznacza y = x + 1.

Jeśli ten wynik zostanie zastąpiony w równaniu równości modułów, to:

(x + 4)^2 + (x + 1 + 3)^2 = 18

Uproszczenie to:

2 (x+4)^2 = 18, 

Co jest równoważne:

(x+4)^2 = 9

To znaczy x+4 = 3, co oznacza, że ​​x = -1. Tak, że współrzędne D to (-1, 0).

sprawdzać

Komponenty wektorowe Ab Są (-1-(-4); 4-1) = (3; 3)

Może ci służyć: Twierdzenie Thévenin: co polega na aplikacjach i przykładach

i te z wektora płyta CD Są (-1-(-4)); 0 -(-3)) = (3; 3)

Co oznacza, że ​​wektory to sprzęt. Jeśli dwa wektory mają te same komponenty kartezjańskie mają ten sam moduł i kierunek, dlatego są to sprzęt.

-Ćwiczenie 3

Wolny wektor Lub ma wielkość 5 i adres 143 1301º.

Znajdź jego komponenty kartezjańskie i określ współrzędne punktów B i C, wiedząc, że stałe wektory AB i CD są wyposażeniem. Współrzędne A to (0, 0), a współrzędne punktu C to (-3,2).

Rozwiązanie 

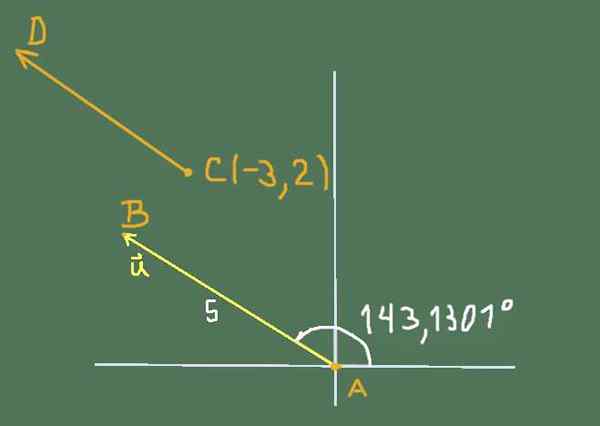
Sytuację zaproponowaną przez ćwiczenie może być reprezentowana przez następujący rysunek:

Rysunek 2. Schemat rozwiązywania ćwiczeń 3. Źródło: Self Made.

Komponenty kartezjańskie Lub Czy

Lub = (5*cos (143,1301º); 5*sin (143,1301º))) 

Wykonanie obliczeń pozostaje:

Lub = (-4; 3) 

B Współrzędne są nieznane, więc umieścimy B (x, y)

Współrzędne wektora Ab Są (X-0; Y-0), ale ponieważ jest to sprzęt z u, musi być wypełniona równość komponentów, stwierdza się zatem, że współrzędne B wynoszą (-4, 3).

Podobnie współrzędne wektora płyta CD Są (x-(-3)); (i - 2) To musi być sprzęt u, llub to prowadzi do:

 x + 3 = -4 i y -2 = 3

Wówczas współrzędne punktu D będą (-7, 5).

Bibliografia

  1. Obliczenie.DC. Stały wektor. Wolny wektor. Odzyskane z: Obliczanie.DC
  2. 2D Descartes. Stałe wektory i wolne wektory płaszczyzny. Źródło: Zasoby.Edukacja.Jest
  3. Projekt GUAO. Equipocent wektory. Odzyskane z: guao.org
  4. Resnick, r., Krane, k. (2001). Fizyka (w języku angielskim). Nowy Jork: John Wiley & Sons.
  5. Serway, r.; Jewett, John W. (2004). Fizyka dla naukowców i inżynierów (w języku angielskim) (wydanie 6). Brooks/Cole.
  6. Tupler, Paul A. (2000). Fizyka nauk i technologii. Tom I. Barcelona: Ed. Odwróciłem się.
  7. Weisstein, e. "Wektor". W Weisstein, Eric W. Mathworld (w języku angielskim). Wolfram Research.