Normalne obliczenia i przykładowy wektor

On Normalny wektor Jest to taki, który określa kierunek prostopadły do ​​rozważanego jednostki geometrycznej, która może być na przykład dla krzywej, płaszczyzny lub powierzchni.

Jest to bardzo przydatna koncepcja w pozycjonowaniu cząstki mobilnej lub jakiejś powierzchni w przestrzeni. Na poniższym wykresie można zobaczyć, jak normalny jest wektor do dowolnej krzywej C:

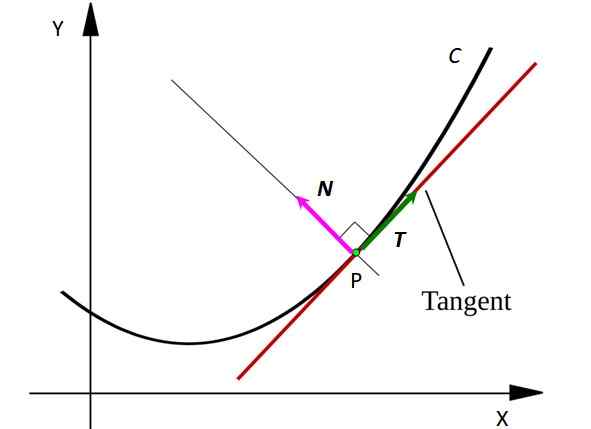
Rysunek 1. Krzywa C z normalnym wektorem do krzywej w punkcie P. Źródło: SVJO [CC BY-SA 3.0 (https: // creativeCommons.Org/licencje/by-sa/3.0)]

Rozważ punkt P na krzywej C. Punkt może reprezentować cząsteczkę ruchomą, która porusza się po drodze w kształcie c. Linia styczna do krzywej w punkcie P pojawia się na czerwono.

Zauważ, że wektor T Jest styczny do C w każdym punkcie, podczas gdy wektor N jest prostopadle do T i wskazuje na środek wyimaginowanego obwodu, którego łukiem jest odcinek C. Wektory są oznaczone odważną literą w drukowanym tekście, aby odróżnić je od innych wielkości nie -wektorowych.

Wektor T Zawsze wskazuje, gdzie porusza się cząstka, dlatego wskazuje na prędkość tego samego. Zamiast tego wektor N Zawsze wskazują w kierunku, w którym cząstka się obraca, w ten sposób wskazuje na wklęsłość krzywej C.

[TOC]

Jak doprowadzić normalny wektor do płaszczyzny?

Normalny wektor niekoniecznie jest wektorem jednostkowym, to znaczy wektorem, którego moduł wynosi 1, ale jeśli tak, jest nazywany Normalny wektor jednostki.

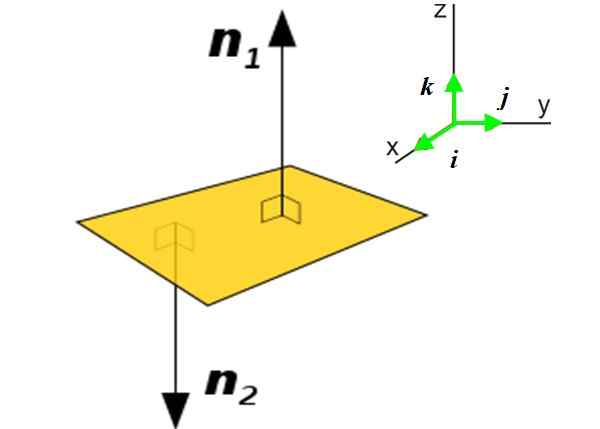
Rysunek 2. Po lewej płaszczyznę P i dwa normalne wektory do wspomnianego samolotu. Po prawej wektory jednostkowe w trzech kierunkach, które określają przestrzeń. Źródło: Wikimedia Commons. Zobacz stronę dla autora [domena publiczna]

W wielu zastosowaniach należy znać normalny wektor do płaszczyzny zamiast krzywej. Ten wektor przedstawia orientację wspomnianej płaszczyzny w kosmosie. Rozważmy na przykład samolot P (żółty) figury:

Może ci służyć: gemine: pochodzenie, cechy i sposób ich obserwowania

W tej płaszczyźnie są dwa normalne wektory: N₁ I N₂. Użycie jednego lub drugiego będzie zależeć od kontekstu, w którym można znaleźć wspomniany samolot. Uzyskanie normalnego wektora do płaszczyzny jest bardzo proste, jeśli jego równanie jest znane:

ax + przez + cZ + d = 0, z Do, B, C I D liczby rzeczywiste.

Cóż, normalny wektor płaszczyzny jest podany przez:

N = a Siema + B J + C k

Tutaj wektor N wyraża się w kategoriach wektorów jednostkowych i prostopadle do siebie Siema, J I k, skierowane w trzech kierunkach, które określają przestrzeń X i Z, Patrz Rysunek 2 Prawo.

Normalny wektor z produktu wektorowego

Bardzo prosta procedura znalezienia normalnego wektora wykorzystuje właściwości produktu wektora między dwoma wektorami.

Jak wiadomo, trzy różne punkty, a nie kolineal ze sobą, określają płaszczyznę P. Teraz możliwe jest uzyskanie dwóch wektorów Lub I v które należą do wspomnianego samolotu o tych trzech punktach.

Gdy wektory są, Produkt wektorowy Lub X v Jest to operacja, której wynik jest wektorem, który ma właściwość bycia prostopadłą do płaszczyzny określonej przez Lub I v.

Znany ten wektor, jest on oznaczony jako N, I z niego będzie możliwe określenie równania płaszczyzny dzięki równaniu wskazanemu w poprzednim rozdziale:

N = Lub X v

Poniższy rysunek ilustruje opisaną procedurę:

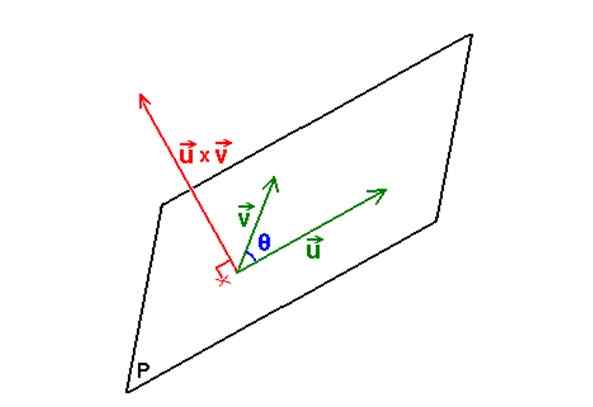Rysunek 3. Z dwoma wektorami i ich wektorem lub produktem krzyżowym określono równanie płaszczyzny zawierające dwa wektory. Źródło: Wikimedia Commons. Nie dostarczył autora, który można odczytać w maszynie. M.Przyjął Romero Schmidtke (na podstawie roszczeń dotyczących praw autorskich). [Domena publiczna]

Przykład

Znajdź równanie płaszczyzny określone przez punkty A (2,1,3); B (0,1,1); C (4,2,1).

Może ci służyć: równanie ciągłości

Rozwiązanie

To ćwiczenie ilustruje procedurę opisaną powyżej. Mając 3 punkty, jeden z nich jest wybrany jako wspólne pochodzenie dwóch wektorów należących do płaszczyzny określonej przez te punkty. Na przykład punkt A jest ustawiony jako pochodzenie i wektory są budowane Ab I AC.

Wektor Ab To wektor, którego pochodzenie jest punktem A i którego koniec jest punktem B. Współrzędne wektora Ab Współrzędne B współrzędnych A:

Ab = (0-2) Siema + (1-1) J + (1-3) k = -2Siema + 0J -2 k

Kontynuuj w ten sam sposób, aby znaleźć wektor AC:

AC = (4-2) Siema + (2-1) J + (1-3) k = 2Siema + J -2 k

Obliczanie produktu wektorowego AB x AC

Istnieje kilka procedur, aby znaleźć produkt wektorowy między dwoma wektorami. W tym przykładzie stosuje się procedurę mnemoniczną, która wykorzystuje poniższą liczbę w celu znalezienia produktów wektorowych wśród wektorów jednostkowych Siema, J I K:

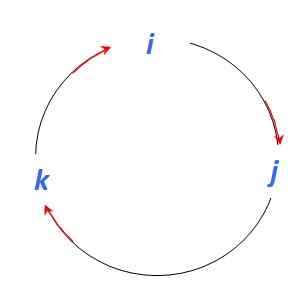Rysunek 4. Grafika w celu określenia produktu wektorowego między wektorami jednostkowymi. Źródło: Self Made.

Na początek dobrze jest pamiętać, że produkty wektorowe między równoległymi wektorami są nieważne, dlatego:

Siema X Siema = 0; J X J = 0; k X k = 0

A ponieważ produkt wektorowy jest kolejnym wektorem prostopadłym do uczestniczących wektorów, zmierzających w kierunku czerwonej strzałki:

Siema X J = k ; J X k = Siema; k X Siema = J

Jeśli musisz poruszać się wbrew strzałce, dodaje się znak (-):

J X Siema = - k; k X J = -Siema; Siema X k = -J

W sumie możliwe jest wykonanie 9 produktów wektorowych z wektorami jednostkowymi Siema, J I k, z czego 3 będzie nieważne.

Ab X AC = (-2Siema + 0J -2 k) X (2Siema + J -2 k) = -4 (Siema X Siema) -2 (Siema X J) +4 (Siema X k) +0 (J X Siema) + 0 (J X J) - 0 (J X k) - 4 (k X Siema) -2 (k X J) + 4 (k X k) = -2k-4J-4J+2Siema = 2Siema -8J-2k

Równanie płaskie

Wektor N został określony przez wcześniej obliczony produkt wektorowy:

Może ci służyć: ruch wahadłowy

N = 2Siema -8J-2k

Dlatego a = 2, b = -8, c = -2, poszukiwany plan to:

AX + przez + CZ + D = 0 → 2x-8y-2z + d = 0

Wartość D. Jest to łatwe, jeśli wartości jednego z punktów a, b lub c są dostępne w równaniu płaskim. Wybór C na przykład:

x = 4; y = 2; Z = 1

Zostaje:

2.48.2 - 2.1 + D = 0

-10 + D = 0

D = 10

Krótko mówiąc, pożądany samolot to:

2x-8y-2z +10 = 0

Czytelnik dociekliwy może zapytać, czy ten sam wynik zostałby uzyskany, gdyby zamiast tego robić Ab X AC Zostałby wybrany AC X Ab. Odpowiedź brzmi tak, płaszczyzna określona przez te trzy punkty jest unikalna i ma dwa normalne wektory, jak pokazano na rycinie 2.

Jeśli chodzi o wybrany punkt jako pochodzenie wektorów, nie ma również niedogodności przy wyborze żadnego z pozostałych dwóch.

Bibliografia

1. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB). 31-62.
2. Znalezienie normalnej do płaszczyzny. Źródło: Web.mama.Utexas.Edu.
3. Larson, r. (1986). Obliczenia i geometria analityczna. MC Graw Hill. 616 - 647.
4. Linie i plany w R 3. Odzyskane z: matematyki.Harvard.Edu.
5. Normalny wektor. Odzyskane z Mathworld.Wolfram.com.