Zmienne statystyczne

Jakie są zmienne statystyczne?

Zmienne statystyczne są cechami, które posiadają ludzie, rzeczy lub miejsca, które można zmierzyć. Przykładami często stosowanych zmiennych są wiek, waga, wysokość, płeć, status cywilny, poziom akademicki, temperatura, liczba godzin, które trwają żarówkę i wiele innych i wiele innych.

Jednym z celów nauki jest wiedza o tym, jak zachowują się zmienne systemu, aby móc przewidywać jego przyszłe zachowanie. Zgodnie z jego charakterem każda zmienna wymaga konkretnego leczenia, aby uzyskać z niej maksymalne informacje.

Ilość zmiennych do badania jest ogromna, ale dokładnie badając wyżej wspomnianą grupę, natychmiast zauważamy, że niektóre można wyrazić numeryczne, podczas gdy inne nie.

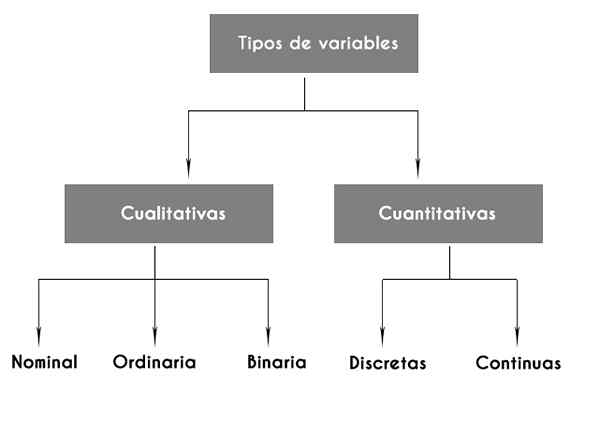
Daje nam to początkową klasyfikację zmiennych statystycznych w dwóch typach podstawowych: jakościowych i numerycznych.

Rodzaje zmiennych statystycznych

- Zmienne jakościowe

Jak sama nazwa wskazuje, zmienne jakościowe są używane do oznaczania kategorii lub cech.

Dobrze znanym przykładem tego typu zmiennych jest status cywilny: singiel, żonaty, rozwiedziony lub wdowiec. Żadna z tych kategorii nie jest większa od drugiej, nie określa tylko innej sytuacji.

Więcej tego typu to:

-Poziom akademicki

-Rok roku

-Prowadzona marka samochodowa

-Zawód

-Narodowość

-Kraje, miasta, dzielnice, powiaty i inne podziały terytorialne.

Kategorię można również wyznaczyć liczbą, na przykład numer telefonu, numer domu, ulica lub kod pocztowy, bez tego, że to ocena liczbowa, ale raczej etykieta.

Numer ulicy jest zmienną jakościową, nie jest zmienną ilościową

Zmienne nominalne, porządkowe i binarne

Zmienne jakościowe mogą z kolei następować:

-Nominalny, które przypisują nazwę do jakości, na przykład kolor.

-Orderał, które reprezentują porządek, jak w przypadku skali warstw społeczno -ekonomicznych (wysokie, średnie, niskie) lub opinie na temat pewnego rodzaju propozycji (na korzyść, obojętne, przeciw). *

Może ci służyć: stopnie swobody: jak je obliczyć, typy, przykłady

-Dwójkowy, Nazywane również dychotomiczny, Istnieją tylko dwie możliwe wartości, takie jak seks. Tę zmiennej można przypisać etykietom numeryczne, taką jak 1 i 2, bez reprezentowania oceny numerycznej lub pewnego rodzaju kolejności.

*Niektórzy autorzy obejmują zmienne porządkowe w grupie zmiennych ilościowych, które opisano poniżej. To dlatego, że wyrażają porządek lub hierarchię.

- Zmienne numeryczne lub ilościowe

Zmienne te przypisane są liczba, ponieważ reprezentują kwoty, takie jak wynagrodzenie, wiek, odległości i kwalifikacje uzyskane na egzaminie.

Są szeroko stosowane do kontrastu preferencji i szacowania trendów. Mogą być powiązane ze zmiennymi jakościowymi oraz słupkami budowlanymi i histogramami, które ułatwiają analizę wizualną.

Niektóre zmienne numeryczne można przekształcić w zmienne jakościowe, ale odwrotnie nie jest możliwe. Na przykład zmienna numeryczna „wiek” można podzielić na przedziały z przypisanymi etykietami, takimi jak dzieci, dzieci, młodzież, dorośli i osoby starsze.

Należy jednak zauważyć, że istnieją operacje, które można wykonać za pomocą zmiennych numerycznych, których oczywiście nie można przeprowadzić z jakościowymi, na przykład obliczając średnie i inne estymatory statystyczne.

Jeśli chcesz obliczyć, musisz utrzymać zmienną „wiek” jako zmienną numeryczną. Ale inne aplikacje mogą nie wymagać szczegółów numerycznych, ponieważ wystarczy, aby zostawić wymienione etykiety.

Zmienne numeryczne są z kolei podzielone na dwie główne kategorie: zmienne dyskretne i zmienne ciągłe.

Zmienne dyskretne

Zmienne dyskretne przyjmują tylko pewne wartości i charakteryzują się rozliczaniem, na przykład liczba dzieci rodziny, ilość zwierząt domowych, liczba klientów, którzy odwiedzają sklep codziennie i subskrybentów firmy kablowej, aby wspomnieć Kilka przykładów.

Może ci służyć: minimalne kwadraty

Definiując na przykład zmienną „liczbę zwierząt”, przyjmuje swoje wartości zestawu liczb naturalnych. Osoba może mieć 0, 1, 2, 3 lub więcej zwierząt, ale nigdy 2.Na przykład 5 zwierząt domowych.

Jednak dyskretna zmienna koniecznie ma naturalne lub liczbowe. Liczby dziesiętne również służą, ponieważ kryterium ustalenia, czy zmienna jest dyskretna, jest to, że jest to rozliczanie lub ponumerowane.

Załóżmy na przykład, że ułamek wadliwych żarówek jest zdefiniowany jako zmienna.

Jeśli żadna żarówka nie jest wadliwa, zmienna przyjmuje wartość 0. Ale jeśli 1 z N żarówek jest wadliwe, zmienna jest warta 1 /n, jeśli istnieją dwie wadliwe, to 2 /n i tak dalej, aż do osiągnięcia zdarzenia, że ​​N żarówki były wadliwe, aw takim przypadku ułamek wynosiłby 1.

Zmienne ciągłe

W przeciwieństwie do zmiennych dyskretnych, zmienne ciągłe mogą przybierać dowolną wartość. Na przykład waga studentów, którzy badają określony temat, wysokość, temperatura, czas, długość i wiele innych.

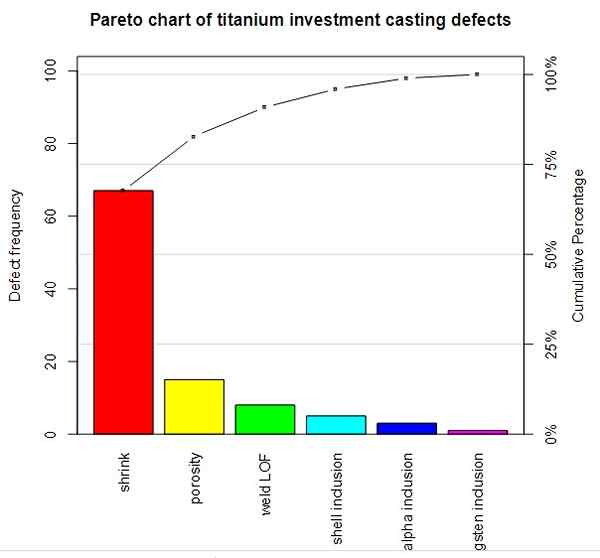Schemat Pareto porównujący częstotliwość defektu (zmienna ilościowa w osi pionowej) i procent skumulowany w porównaniu z każdą wadą w osi poziomej (zmienna jakościowa). Źródło: Wikimedia Commons.

Ponieważ zmienna ciągła przyjmuje nieskończone wartości, wszelkiego rodzaju obliczenia można wykonać z pożądaną precyzją, po prostu dostosowując liczbę dziesiętnych dziesiętnych.

W praktyce istnieją zmienne ciągłe, które można wyrażać jako zmienne dyskretne, na przykład wiek osoby.

Dokładny wiek osoby można policzyć w latach, miesiącach, tygodniach, dniach i innych, w zależności od pożądanej precyzji, ale zwykle okrążenia od lat, a zatem staje się dyskretny.

Dochód osoby jest również zmienną ciągłą, ale zwykle działa lepiej, jeśli ustalone są odstępy.

Może ci służyć: stopień wielomianu: jak jest to ustalone, przykłady i ćwiczenia

- Zmienne zależne i niezależne

Zmienne zależne to zmierzone podczas eksperymentu, aby zbadać związek, jaki mają z innymi, które byłyby uważane za zmienne niezależne.

Przykład 1

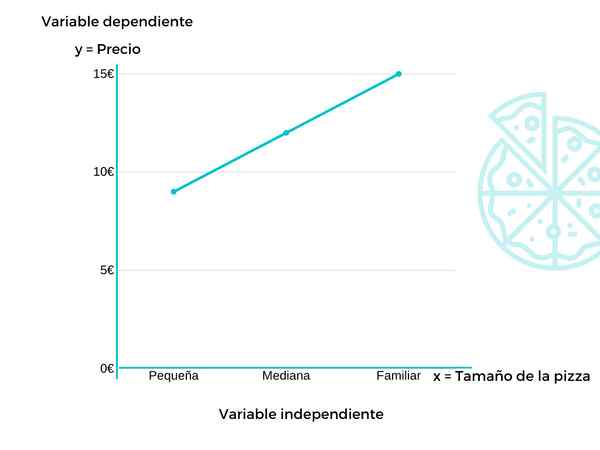
W tym przykładzie zobaczymy ewolucję cen cierpiących na pizze miejsca żywności w zależności od jego wielkości.

Zmienną zależną (y) byłaby cena, podczas gdy zmienna niezależna (x) byłaby rozmiarem. W tym przypadku mała pizza jest warta 9 €, mediana 12 € i znane 15 €.

Oznacza to, że wraz ze wzrostem wielkości pizzy kosztuje więcej. Dlatego cena byłaby zależna od wielkości.

Ta funkcja wynosiłaby y = f (x)

Przykład 2

Prosty przykład: chcesz zbadać efekt zmieniający się w prądu, który wytwarzam przez drut metalowy, dla którego mierzone jest napięcie V między końcami tego.

Zmienna niezależna (przyczyna) jest prąd, podczas gdy zmienna zależna (efekt) jest napięciem, którego wartość zależy od prądu, który przesuwa się przez drut.

W eksperymencie poszukiwane jest wiedzieć, jak wygląda prawo, gdy jestem zróżnicowany. Jeśli zależność napięcia z prądem okazuje się liniowa, to znaczy: v ∝ i, sterownik jest omowy, a stałą proporcjonalności jest opór drutu.

Ale fakt, że zmienna jest niezależna w eksperymencie, nie oznacza, że ​​jest w innym. Będzie to zależeć od badanego zjawiska i rodzaju badań, które chcesz przeprowadzić.

Na przykład prąd I, który podróżuje zamkniętym sterownikiem obracającym się w stałym polu magnetycznym, staje się zmienną zależną w odniesieniu do czasu t, która stałaby się zmienną niezależną.

Bibliografia

1. Berenson, m. 1985. Statystyka administracji i ekonomii. Inter -American s.DO.
2. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
3. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
4. Ekonomiczne encyklopedia. Zmienne ciągłe. Odzyskane z: Encyclopediaeconomica.com.
5. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
6. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.