Stopnie swobody, jak je obliczyć, typy, przykłady

 stopnie swobody W statystykach jest liczba niezależnych elementów losowego wektora. Jeśli wektor ma N komponenty i są P równania liniowe, które dotyczą jego komponentów, a następnie stopień wolności To jest n-p.

Koncepcja stopnie swobody Pojawia się również w mechanice teoretycznej, gdzie w trybie brutto są one równoważne wymiarowi przestrzeni, w której porusza się cząsteczka, z wyjątkiem liczby ligatury.

Rysunek 1. Wahadło porusza się w dwóch wymiarach, ale ma tylko pewien stopień swobody, ponieważ jest zobowiązany do poruszania się w promieniu. Źródło: f. Zapata.

W tym artykule omówiono koncepcję stopni swobody zastosowanej do statystyk, ale mechaniczny przykład jest łatwiejszy do wizualizacji w sposób geometryczny.

[TOC]

Rodzaje stopnia wolności

Zgodnie z kontekstem, w którym jest stosowany, sposób obliczania liczby stopni swobody może się różnić, ale podstawowa idea jest zawsze taka sama: całkowite wymiary mniejsze liczba ograniczeń.

W przypadku mechanicznym

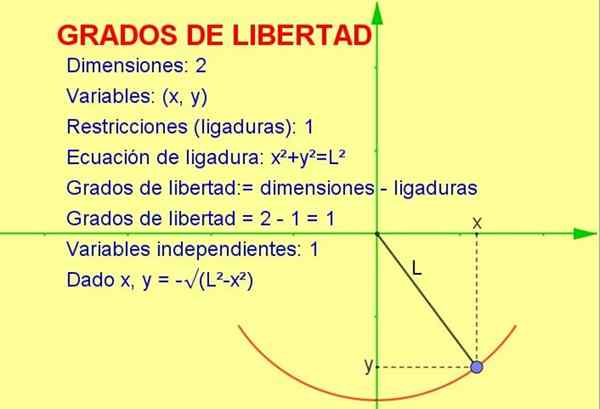
Rozważ cząsteczkę, która oscyluje przywiązane do liny (wahadła), która porusza się w płaszczyźnie pionowej x-y (2 wymiary). Jednak cząstka jest zobowiązana do poruszania się po obwodzie promienia równa długości liny.

Ponieważ cząstka może poruszać się tylko po tej krzywej, liczba stopnie swobody To jest 1. Można to wizualizować na rycinie 1.

Sposobem obliczenia liczby stopni swobody jest wprowadzenie różnicy w liczbie wymiarów, z wyjątkiem liczby ograniczeń:

Stopnie swobody: = 2 (wymiary) - 1 (ligacja) = 1

Kolejnym wyjaśnieniem, które pozwala nam osiągnąć wynik, jest następujące:

-Wiemy, że położenie dwóch wymiarów jest reprezentowane przez punkt współrzędnej (x, y).

-Ale ponieważ punkt musi wypełnić równanie obwodu (x² + I² = L²) Dla danej wartości zmiennej x zmienna i jest określana przez wspomniane równanie lub ograniczenie.

W ten sposób tylko jedna z zmiennych jest niezależna, a system ma Jeden (1) stopień wolności.

Może ci służyć: klasyczne prawdopodobieństwo: obliczenia, przykłady, rozwiązane ćwiczenia

W zestawie losowych wartości

Aby zilustrować, co oznacza koncepcja, przypuśćmy wektor

X = (x₁, X₂,…, X_N)

Reprezentując próbkę N Wartości losowe normalnie rozmieszczone. W tym przypadku losowy wektor X ma N niezależne komponenty i dlatego mówi się, że X ma n stopnie wolności.

Zbudujmy teraz wektor R odpadów

R = (x₁ - , X₂ - ,.. ., X_N - )

Gdzie reprezentuje średnią próbki, która jest obliczana w następujący sposób:

= (x₁ + X₂ +.. .+ X_N) / N

Następnie suma

(X₁ - )+(x₂ - )+.. .+(X_N - ) = (x₁ + X₂ +.. .+ X_N) - n = 0

Jest to równanie reprezentujące ograniczenie (lub podwiązanie) w elementach wektorowych R odpadów, ponieważ jeśli n-1 są znane, elementy wektorowe R, Równanie ograniczenia określa nieznany komponent.

Dlatego wektor R wymiaru n z ograniczeniem:

∑ (x_Siema - ) = 0

Ma (N - 1) stopnie wolności.

Ponownie stosuje się, że obliczanie liczby stopni wolności wynosi:

Stopnie swobody: = n (wymiary) - 1 (ograniczenia) = n -1

Przykłady

Wariancja i stopnie wolności

Wariancja s² Jest zdefiniowany jako średnia kwadratu odchyleń (lub odpadów) próbki danych:

S² = (R• •R) / (N-1)

Gdzie R to wektor odpadów R = (x1 -, x2 -, .. ., Xn -) i gruby punkt (• •) jest operatorem produktu skalarnego. Alternatywnie formuła wariancji można zapisać w następujący sposób:

S² = ∑ (x_Siema - )² / (N-1)

W każdym razie należy zauważyć, że przy obliczaniu średniej kwadratu odpadów jest on podzielony przez (n-1), a nie między n, ponieważ jak omówiono w poprzedniej sekcji, liczba stopni wolności wolności wektor R IS (n-1).

Jeśli do obliczania wariancji został podzielony między N Zamiast (n-1) wynik miałby odchylenie, które jest bardzo istotne dla wartości N mniej niż 50.

Może ci służyć: geometria analityczna

W literaturze pojawia się również formuła wariancji z dzielnikiem n zamiast (n-1), jeśli chodzi o wariancję populacji.

Ale zbiór losowej zmiennej odpadów, reprezentowany przez wektor R, Chociaż ma wymiar n, ma tylko (n-1) stopnie wolności. Jeśli jednak numer danych jest wystarczająco duży (n> 500), oba wzory zbieżają się do tego samego wyniku.

Kalkulatory i arkusze kalkulacyjne oferują dwie wersje wariancji i odchylenie standardowe (które jest pierwiastkiem kwadratowym wariancji).

Naszym zaleceniem, z uwagi na przedstawioną tutaj analizę, jest zawsze wybór wersji z (n-1) za każdym razem, gdy konieczne jest obliczenie wariancji lub odchylenia standardowego, aby uniknąć wyników z uprzedzeniami.

W rozkładu Chi Square

Niektóre rozkłady prawdopodobieństwa w ciągłej zmiennej losowej zależą od parametru o nazwie stopień wolności, Tak jest w przypadku rozkładu kwadratu chi (χ²).

Nazwa wspomnianego parametru pochodzi tylko z stopni swobody losowego wektora, do którego zastosowano ten rozkład.

Załóżmy, że istnieją pop populacje, z których pobiera próbki n wielkości:

X₁ = (x1₁, x1₂,... x1_N)

X2 = (x2₁, x2₂,... x2_N)

.. .

X_J = (XJ₁, xj₂,… XJ_N)

.. .

Xg = (xg₁, Xg₂,… Xg_N)

Populacja J to ma średnio i standardowe odchylenie Sj, Postępuj zgodnie z rozkładem normalnym N (, Sj ).

Typowa lub znormalizowana zmienna ZJ_Siema jest definiowany jako:

ZJ_Siema = (XJ_Siema - ) / Sj.

I wektor ZJ Jest tak zdefiniowany:

ZJ = (ZJ₁, ZJ₂,…, ZJ_Siema,…, ZJ_N) I podążaj za rozkładem normalnym N (0,1).

Następnie zmienna:

Q = ((Z1₁ ^2 + Z2₁^2+… . + Z G₁^2),… ., (Z1_N^2 + Z2_N^2+… . + Z G_N^2))

Postępuj zgodnie z rozkładem χ²(g) nazywane Dystrybucja Chi Square ze stopniem swobody G.

W kontrastu hipotez (z rozwiązanym przykładem)

Jeśli chcesz skontrastować hipotezę oparte na określonym zestawie danych losowych, konieczne jest znanie liczba stopni wolności g Aby móc zastosować test Chi Square.

Może ci służyć: ciągła jednolita dystrybucja: cechy, przykłady, aplikacje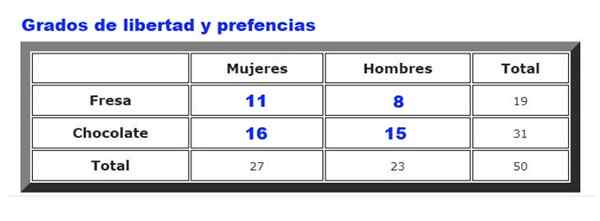 Rysunek 2. Czy istnieje związek między smakiem lodów a płcią klientów? Źródło: f. Zapata.

Jako przykład, dane zebrane na czekoladzie lub preferencjach lodów truskawkowych między mężczyznami i kobietami w niektórych lodach będą przeanalizowane. Częstotliwość, z jaką mężczyźni i kobiety wybierają truskawkę lub czekoladę, podsumowano na rycinie 2.

Po pierwsze, obliczana jest oczekiwana tabela częstotliwości, która jest wykonana przez pomnożenie Całkowite wiersze dla niego Całkowite kolumny, podzielony przez Całkowite dane. Wynik pokazano na poniższym rysunku:

Rysunek 3. Obliczanie oczekiwanych częstotliwości na podstawie obserwowanych częstotliwości (wartości niebieskie na rycinie 2). Źródło: f. Zapata.

Następnie obliczamy kwadrat chi (na podstawie danych) według następującego wzoru:

χ² = ∑ (f_albo - F_I)² / F_I

Gdzie f_albo są obserwowanymi częstotliwościami (ryc. 2) i F_I to oczekiwane częstotliwości (ryc. 3). Suma jest na wszystkich szeregach i kolumnach, co w naszym przykładzie dają cztery warunki.

Po przeprowadzeniu operacji otrzymujesz:

χ² = 0,2043.

Teraz konieczne jest porównanie z placem teoretycznym, który zależy od liczba stopni wolności g.

W naszym przypadku liczba ta jest określana w następujący sposób:

G = (#filas - 1) (#Columnas - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Okazuje się, że liczba stopni wolności g tego przykładu wynosi 1.

Jeśli chcesz zweryfikować lub odrzucić hipotezę zerową (H0: nie ma korelacji między smakiem a płcią) z poziomem istotności 1%, teoretyczny kwadrat chi oblicza się z stopniem swobody g = 1.

Wartość, która powoduje, że nagromadzona częstotliwość jest poszukiwana (1–0.01) = 0.99, to 99%. Ta wartość (którą można uzyskać z tabel) wynosi 6.636.

Gdy teoretyczne chi przekracza obliczone, wówczas hipoteza zerowa jest weryfikowana.

To znaczy wraz ze zebranymi danymi, nie ma związku między smakiem zmiennym a płcią.

Bibliografia

1. Minitab. Jakie są stopnie wolności? Źródło: wsparcie.Minitab.com.
2. Moore, David. (2009) Podstawowe statystyki stosowane. Redaktor Antoni Bosch.
3. Leigh, Jennifer. Jak obliczyć stopnie swobody w modelach statystycznych. Odzyskane z: Geniolandia.com
4. Wikipedia. Stopień swobody (statystyki). Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Stopień wolności (fizyczny). Odzyskane z: jest.Wikipedia.com