Dane nie zgrupowane przykłady i rozwiązywane ćwiczenia

Dane bez grupy Są to te, które uzyskane z badania nie są jeszcze zorganizowane przez klasy. Gdy jest to możliwa do zarządzania liczba danych, zwykle 20 lub mniej, i istnieje kilka różnych danych, można je traktować jako nie zgrupowane i wydobywać z nich cenne informacje.

Dane niezgrupowe pochodzą z ankiety lub badania przeprowadzonego w celu ich uzyskania, a zatem brak przetwarzania. Spójrzmy na kilka przykładów:

Rysunek 1. Dane niezgrupowe pochodzą bezpośrednio z dowolnego badania i nie zostały sklasyfikowane. Źródło: Pxhere.

-Wyniki egzaminu CI współczynnika intelektualnego u 20 przypadkowych studentów z uniwersytetu. Uzyskane dane były następująco:

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112,106

-W wieku 20 pracowników bardzo popularnej kawiarni:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

-Średnia końcowa notatki 10 uczniów klasy matematyki:

3.2; 3.1; 2,4; 4.0; 3.5; 3.0; 3.5; 3.8; 4.2; 4.9

[TOC]

Właściwości danych

Istnieją trzy ważne właściwości, które charakteryzują zestaw danych statystycznych, są zgrupowane lub nie, które są:

-Pozycja, co jest tendencją do grupowania danych wokół niektórych wartości.

-Dyspersja, Wskazujący na to, jak rozproszone lub rozpowszechnione są dane wokół określonej wartości.

-Kształt, Odnosi się do sposobu dystrybucji danych, co można zobaczyć, gdy ich wykres jest skonstruowany. Istnieją bardzo symetryczne, a także stronnicze krzywe, po lewej lub po prawej stronie określonej wartości centralnej.

Dla każdej z tych właściwości istnieje wiele miar, które je opisują. Po uzyskaniu dają nam panoramę zachowań danych:

-Najczęściej stosowanymi miarami pozycji są średnia arytmetyczna lub po prostu średnia, mediana i moda.

-W dyspersji zakres jest często stosowany wariancja i odchylenie standardowe, ale nie są to jedyne pomiary dyspersji.

Może ci służyć: homotecia

-I aby określić formę, średnia i mediana są porównywane przez stronniczość, co będzie widać wkrótce.

Obliczanie średniej, mediany i mody

-Średnia arytmetyczna, Znany również jako średnia i oznaczona jako x, oblicza się w następujący sposób:

X = (x₁ + X₂ + X₃ +... X_N) / N

Gdzie x₁, X₂,.. . X_N, są danymi, a n to suma. Podsumowując sumę, jest:

Tutaj indeks I reprezentuje dane 1, dane 2, dane 3 itp., Aż do osiągnięcia jedynego, który jest ostatnim.

-Mediana Jest to wartość, która pojawia się w połowie uporządkowanej sukcesji danych, aby je uzyskać, konieczne jest zamówienie danych najpierw.

Jeśli liczba obserwacji jest dziwna, nie ma problemu z znalezieniem punktu środkowego zestawu, ale jeśli mamy parę danych, dwa centralne dane są poszukiwane i uśrednione.

-Moda Jest to najczęstsza wartość obserwowana w zestawie danych. Nie zawsze istnieje, ponieważ możliwe jest, że żadna wartość nie jest powtarzana częściej niż inna. Mogą być również dwa dane o równej częstotliwości, w którym to przypadku mówi się o rozkładu dwumicznym.

W przeciwieństwie do dwóch poprzednich miar, moda można wykorzystać z danymi jakościowymi.

Zobaczmy, w jaki sposób te miary pozycji są obliczane na przykład:

Rozwiązany przykład

Załóżmy, że chcesz określić średnią arytmetyczną, medianę i modę w przykładzie zaproponowanym na początku: w wieku 20 pracowników kawiarni:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

połowa Jest to obliczane po prostu przez dodanie wszystkich wartości i dzielenie przez n = 20, co jest całkowitą liczbą danych. Tą drogą:

Może ci służyć: Relacje proporcjonalne: koncepcja, przykłady i ćwiczenia

X = (24 + 20 + 22 + 19 + 18 + 27+ 25 + 19 + 27 + 18 + 21 + 22 + 23 + 21+ 19 + 22 + 27+ 29 + 23+ 20) / 20 =

= 22.3 lata.

Znaleźć mediana Konieczne jest najpierw zamówienie zestawu danych:

18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 22, 23, 23, 24, 25, 27, 27, 27, 29

Podobnie jak kilka danych, dwa centralne dane, wyróżnione pogrubione, są pobierane i uśrednione. Ponieważ oba mają 22 lata, mediana to 22 lata.

Wreszcie moda Jest to fakt, że jest powtarzany najbardziej lub że częstotliwość jest większa, ponieważ to 22 lata.

Zakres, wariancja, odchylenie standardowe i odchylenie

Zakres jest po prostu różnicą między główną a najmniejszą ilością danych i pozwala ich zmienności szybko docenić. Ale poza tym istnieją inne środki dyspersji, które zawierają więcej informacji na temat dystrybucji danych.

Wariancja i odchylenie standardowe

Wariancja jest oznaczona jako s i jest obliczana według wyrażenia:

Często działa z quasirance zamiast wariancji, która jest obliczana w ten sam sposób, podzielony tylko przez N-1, zamiast robić między N:

Ponieważ wariancja jest sumą kwadratów, powoduje kwadrat jednostki próbki. Na przykład w badaniu wieków pracowników w stołówce wariancja nastąpi za lata².

Następnie, aby słusznie zinterpretować wyniki, definiuje się odchylenie standardowe, takie jak pierwiastek kwadratowy wariancji lub również standardowe quasi-oddziaływanie, które jest pierwiastkiem kwadratowym Quasivarian:

Stronniczość

Jest to porównanie średniej x i mediany Med:

-Tak Med = Media X: Dane są symetryczne.

-Kiedy x> med: stronniczy w prawo.

-A jeśli x < Med: los datos sesgan hacia la izquierda.

Ćwiczenie rozwiązane

Znajdź średnią, medianę, modę, rangę, wariancję, odchylenie standardowe i uprzedzenie dla wyników badań współczynnika intelektualnego 20 studentów z uniwersytetu:

Może ci służyć: funkcje matematyczne

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112, 106

Rozwiązanie

Zamówimy dane, ponieważ konieczne będzie znalezienie mediany.

106, 106, 106, 109, 109, 109, 109, 109, 112, 112, 112, 112, 112, 112, 119, 119, 124, 124, 124

I umieścimy je w stole w następujący sposób, aby ułatwić obliczenia. Druga kolumna zatytułowana „Zgromadzona” jest sumą odpowiednich danych plus poprzednie.

Ta kolumna pomoże łatwo znaleźć średnią, dzieląc ostatnią zgromadzenie między całkowitą liczbą danych, jak widać na końcu kolumny „nagromadzonej”:

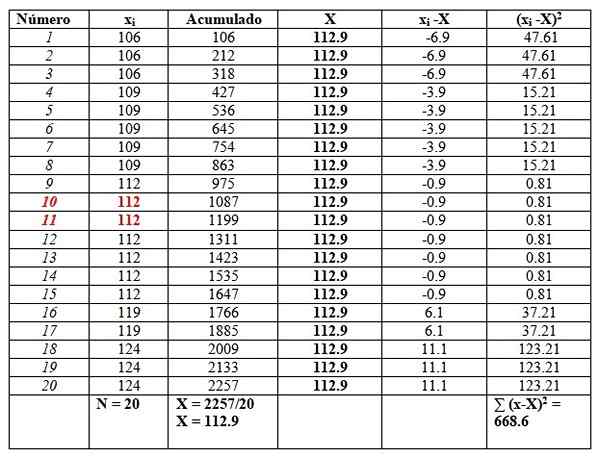
X = 112.9

Mediana to średnia centralnych danych podkreślonych na czerwono: liczba 10 i liczba 11. Podobnie jak ta sama mediana to 112.

Wreszcie moda jest wartością, która jest najbardziej powtarzana i wynosi 112, z 7 powtórzeniami.

Jeśli chodzi o pomiary dyspersji, zakres wynosi:

124-106 = 18.

Wariancję uzyskuje się poprzez podzielenie końcowego wyniku prawej kolumny między N:

S = 668.6/20 = 33.42

W takim przypadku odchyleniem standardowym jest pierwiastkiem kwadratowym wariancji: √33.42 = 5.8.

Z drugiej strony wartości quasiwarianina i quasi odchylenie standardowe to:

S_C= 668.6/19 = 35.2

Standardowe quasi-dewiację = √35.2 = 5.9

Wreszcie, stronniczość jest nieznacznie po prawej, ponieważ średnia 112.9 jest większa niż mediana 112.

Bibliografia

1. Berenson, m. 1985. Statystyka administracji i ekonomii. Inter -American s.DO.
2. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
3. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
4. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
5. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.