Rodzaje aksjomatów prawdopodobieństwa, wyjaśnienie, przykłady, ćwiczenia

aksjomaty prawdopodobieństwo Są to propozycje matematyczne dotyczące teorii prawdopodobieństwa, które nie zasługują na demonstrację. Aksjomaty zostały ustanowione w 1933 r. Przez rosyjskiego matematyka Andrei Kolmogorov (1903–1987) w swojej pracy Podstawy teorii prawdopodobieństwa i położył podstawę badań matematycznych prawdopodobieństwa.

Podczas przeprowadzania pewnego losowego eksperymentu ξ, przestrzeń próbki jest tą wraz ze wszystkimi możliwymi wynikami eksperymentu, zwaną także wydarzenia. Każde wydarzenie jest oznaczone jako a i p (a) to prawdopodobieństwo wydarzenia. Następnie Kolmogorov ustalił, że:

Rysunek 1. Aksjomaty prawdopodobieństwa pozwalają obliczyć prawdopodobieństwo uderzenia hazardu jak ruletka. Źródło: Pixabay.

-Aksjoma 1 (bez negatywności): Prawdopodobieństwo, że każde zdarzenie nastąpi, jest zawsze pozytywne lub zerowe, P (a) ≥0. Gdy prawdopodobieństwo zdarzenia wynosi 0, nazywa się to Niemożliwe wydarzenie.

-Aksjoma 2 (pewność): pod warunkiem, że jakieś zdarzenie należące do e, jego prawdopodobieństwo wystąpienia wynosi 1, co możemy wyrazić jako P (e) = 1. Jest to, co jest znane jako Bezpieczne wydarzenie, Ponieważ podczas przeprowadzania eksperymentu jest wynik z całą pewnością.

-Aksjoma 3 (dodatek): W przypadku dwóch lub więcej niekompatybilnych wydarzeń dwóch do dwóch, powołanych₁, DO₂, DO₃..., prawdopodobieństwo wydarzenia₁ więcej a₂ więcej a₃ I tak dalej, jest to suma prawdopodobieństwa, że ​​każda z nich zdarza się osobno.

Jest to wyrażone jako: P (a₁ U₂ U₃ U ...) = p (a₁) + P (a₂) + P (a₃) +..

Rysunek 2. Niezwykły rosyjski matematyk Andrei Kolmogorov (1903–1987), który położył fundamenty na prawdopodobieństwo aksjomatyczne. Źródło: Wikimedia Commons.

[TOC]

Przykład

Aksjomaty prawdopodobieństwa są szeroko stosowane w wielu aplikacjach. Na przykład:

Pazur lub tachuela zostaje wyrzucona w powietrze, a gdy podłoga spadnie, istnieje opcja upadku z końcówką (u) lub z końcówką (d) (nie rozważymy innych możliwości). Przykładowa przestrzeń tego eksperymentu składa się z tych zdarzeń, a następnie e = u, d.

Może ci służyć: rewolucja stałe: objętość, typy, rozwiązywane ćwiczeniaRysunek 3. W eksperymencie uruchamiania tachueli istnieją dwa zdarzenia o różnych prawdopodobieństwach: upadek z końcówką lub na podłogę. Źródło: Pixabay.

Stosując aksjomaty:

P (e) = 1 (Aksjoma 2)

Ale P (e) = p (u) + p (d) (Aksjoma 3), ponieważ zdarzenia te są wzajemnie niezgodne lub rozłączne. Błąd nie spada z końcówką w górę lub w dół w tym samym czasie, jest to jedno lub drugie, ale nie jedno i drugie, ponieważ rozważane są inne możliwości. Więc:

P (u) + p (d) = 1

P (u) = 1 - p (d)

Jeśli jest równie prawdopodobne, że spadnie z końcówką w górę lub w dół, P (u) = p (d) = ½ (Aksjoma 1). Możliwe jednak, że z powodu budowy i projektowania błędu. Na przykład może to być P (u) = ¾ chwila P (d) = ¼ (Aksjoma 1).

Zauważ, że w obu przypadkach suma prawdopodobieństwa daje 1. Jednak aksjomaty nie wskazują, jak alokować prawdopodobieństwa, przynajmniej nie do końca. Ale potwierdzają, że są to liczby między 0 a 1 i że jak występuje w tym przypadku, suma wszystkich wynosi 1.

Sposoby przypisania prawdopodobieństwa

Aksjomaty prawdopodobieństwa nie stanowią metody przypisywania wartości prawdopodobieństwa. W tym celu istnieją trzy opcje kompatybilne z aksjomatami:

Reguła Laplace'a

Każde zdarzenie przypisuje się to samo prawdopodobieństwo wystąpienia, wówczas prawdopodobieństwo wystąpienia jest zdefiniowane jako:

P (a) = liczba przypadków korzystnych dla zdarzenia A/ Liczba możliwych przypadków

Na przykład, jakie jest prawdopodobieństwo wydobycia asa z talii francuskich kart? Talia ma 52 karty, 13 każdego kija, a są 4 patyki. Każdy kij ma 1, więc w sumie są 4 asy:

P (as) = ​​4/52 = 1/13

Reguła Laplace'a jest ograniczona do skończonych przestrzeni próbek, w których każde zdarzenie jest równie prawdopodobne.

Może ci służyć: dyskretna matematyka

Częstotliwość względna

Tutaj eksperyment musi być powtarzalny, ponieważ metoda opiera się na wykonaniu dużej liczby powtórzeń.

Zróbmy powtórzenia eksperymentu ξ, których uważamy, że n jest liczbą razy, w których występuje określone zdarzenie A, a następnie prawdopodobieństwo, że to zdarzenie nastąpi:

P (a) = lim_{I → ∞} (żaden)

Gdzie Nie dotyczy to względna częstotliwość zdarzenia.

Zdefiniuj p (a) w ten sposób spełnia aksjomaty Kolmogorowa, ale ma niedogodności, że należy wykonać wiele testów, aby prawdopodobieństwo było odpowiednie.

Metoda subiektywna

Osoba lub grupa osób może zgodzić się na przypisanie prawdopodobieństwa wydarzeniu, poprzez własne wyroki. Ta metoda ma wadę, że różne osoby mogą przypisać różne prawdopodobieństwa do tego samego zdarzenia.

Ćwiczenie rozwiązane

W eksperymencie jednocześnie uruchamiania 3 uczciwych walut, uzyskania szans opisanych wydarzeń:

a) 2 twarze i krzyż.

b) 1 twarz i dwa krzyże

c) 3 krzyże.

d) przynajmniej 1 twarz.

Rozwiązanie

Twarze są oznaczone C i krzyżem x. Ale istnieje kilka sposobów na zdobycie dwóch twarzy i krzyża. Na przykład pierwsze dwie monety mogą spaść z twarzą, a trzecia z Cruz. Lub pierwszy może upaść twarz, drugi krzyż i trzecia twarz. I wreszcie pierwszym może być krzyż i pozostałe twarze.

Aby odpowiedzieć na pytania, konieczne jest znanie wszystkich możliwości, które są opisane w narzędziu nazywanym schemat drzewa albo Drzewo prawdopodobieństwa:

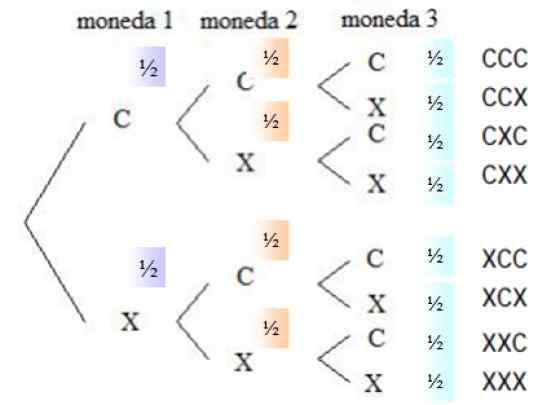Rysunek 4. Schemat drzewa dla jednoczesnego uruchomienia trzech uczciwych monet. Źródło: f. Zapata.

Prawdopodobieństwo, że w każdej walucie jest drogie, wynosi ½, to samo dzieje się dla krzyży, ponieważ waluta jest uczciwa. W prawej kolumnie wszystkie możliwości uruchamiania są wymienione, to znaczy przestrzeń próbki.

Może ci służyć: zmienne statystyczne

Kombinacje odpowiadające na żądane zdarzenie są wybierane z przestrzeni próbki, ponieważ kolejność, w której pojawiają się twarze. Istnieją trzy korzystne zdarzenia: CCX, CXC i XCC. Prawdopodobieństwo każdego zdarzenia wynosi:

P (CCX) = ½. ½ . ½ = 1/8

To samo dzieje się w przypadku zdarzeń CXC i XCC, każde z nich ma 1/8 prawdopodobieństwa wydarzenia. Dlatego prawdopodobieństwo uzyskania dokładnie 2 twarzy jest sumą prawdopodobieństwa wszystkich korzystnych zdarzeń:

P (2 twarze) = 1/8 + 1/8 + 1/8 = 3/8 = 0.375

Rozwiązanie b

Znalezienie prawdopodobieństwa, że ​​istnieją dokładnie dwa krzyże, jest analogicznym problemem do poprzedniej, istnieją również trzy korzystne zdarzenia pobrane z przestrzeni próbki: CXX, XCX i XXC. Dlatego:

P (2 krzyże) = 3/8 = 0.375

Rozwiązanie c

Intuicyjnie wie, że prawdopodobieństwo uzyskania 3 krzyży (lub 3 twarzy) jest niższe. W tym przypadku poszukiwane wydarzenie to XXX, na końcu prawej kolumny, której prawdopodobieństwo to:

P (xxx) = ½. ½. ½ = 1/8 = 0.125.

Rozwiązanie d

Poproszono o uzyskanie co najmniej 1 twarzy, oznacza to, że 3 twarze, 2 twarze lub 1 twarz mogą odejść. Jedynym zdarzeniem niezgodnym z tym jest takie, w którym wychodzą 3 krzyże, których prawdopodobieństwo wynosi 0.125. Dlatego poszukiwane prawdopodobieństwo to:

P (co najmniej 1 twarz) = 1 - 0.125 = 0.875.

Bibliografia

1. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
2. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
3. Lipschutz, s. 1991. Seria Schaum: prawdopodobieństwo. McGraw Hill.
4. Obregón, i. 1989.Teoria prawdopodobieństwa. Limusa redakcyjna.
5. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.