Definicja ogranicznika, typy, wzory, na przykład, do czego służy,

Zmiana lub kurtoza Jest to parametr statystyczny, który służy do scharakteryzowania rozkładu prawdopodobieństwa zmiennej losowej, co wskazuje na stopień stężenia wartości wokół miary centralnej. Jest to również znane jako „ocena szczytowa”.

Termin pochodzi od greckiego „kurtos”, co oznacza łukowate, dlatego ogranicza stopień wskazywania lub spłaszczenia rozkładu, jak pokazano na poniższym rysunku:

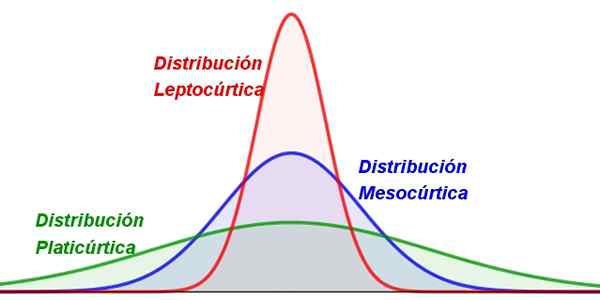Rysunek 1. Różne rodzaje ograniczeń. Źródło: f. Zapata.

Prawie wszystkie wartości zmiennej losowej mają tendencję do grupowania wokół wartości centralnej, takiej jak średnia. Ale w niektórych rozkładach wartości są bardziej rozproszone niż w innych, co powoduje bardziej spłaszczone lub bardziej smukłe krzywe.

[TOC]

Definicja

Zmiana jest wartością liczbową każdego rozkładu częstotliwości, która według stężenia wartości wokół średniej jest podzielona na trzy grupy:

-Leptocuric: w którym wartości są bardzo pogrupowane wokół średniej, więc rozkład jest dość spiczasty i smukły (ryc. 1, po lewej).

-Mesocuric: Ma umiarkowane stężenie wartości wokół średniej (ryc. 1 w środku).

-Phylicuric: Ten rozkład ma szerszy kształt, ponieważ wartości są bardziej rozproszone (ryc. 1 po prawej).

Wzory i równania

Ograniczenie może mieć dowolną wartość, bez ograniczeń. Jego obliczenia są przeprowadzane w zależności od sposobu dostarczania danych. Notacja zastosowana w każdym przypadku jest następująca:

-Współczynnik kortyzowania: G₂

-Średnia arytmetyczna: X lub x z paskiem

-I-em: X_Siema

-Odchylenie standardowe: σ

-Liczba danych: N

-Częstotliwość I-Esimo: F_Siema

-Marka klas: MX_Siema

Dzięki tej notacji przedstawiamy niektóre z najczęściej używanych wzorów, aby znaleźć ograniczenie:

Może ci służyć: przestrzeń wektorowa: podstawa i wymiar, aksjomaty, właściwości

- Ograniczenie zgodnie z prezentacją danych

Bez grupowania lub zgrupowania danych na częstotliwościach

Dane zgrupowane w odstępach czasu

Nadmiar ograniczenia

Nazywane również Współczynnik wskazujący Fishera albo Miara rybaka, Służy do porównania badanego rozkładu z rozkładem normalnym.

Kiedy nadmiar ograniczania jest wart 0, jesteśmy w obecności rozkładu normalnego lub dzwonka Gaussa. W ten sposób, o ile obliczane jest nadmiar opalania rozkładu, w rzeczywistości porównujemy go z rozkładem normalnym.

Zarówno dla danych bez grupowania, jak i dla zgrupowanych danych, współczynnik wskazujący rybaka, oznaczony przez K, wynosi:

K = G₂ - 3

Można jednak wykazać, że ograniczenie rozkładu normalnego wynosi 3, dlatego jeśli współczynnik wskazujący rybaka wynosi 0 lub blisko 0, a rozkład mezokurowy występuje mezokurowy. Jeśli k> 0, rozkład jest lepokurka i jeśli k<0 es platicúrtica.

Czego jest ograniczona?

Curtosis jest miarą zmienności stosowanej do scharakteryzowania morfologii rozkładu. W ten sposób rozkłady symetryczne można porównać z tą samą średnią i równą dyspersją (podawaną przez odchylenie standardowe).

Posiadanie miar zmienności zapewnia, że ​​średnie są wiarygodne i pomaga kontrolować zmiany rozkładu. Jako przykład, przeanalizujmy te dwie sytuacje.

3 wynagrodzenia działów

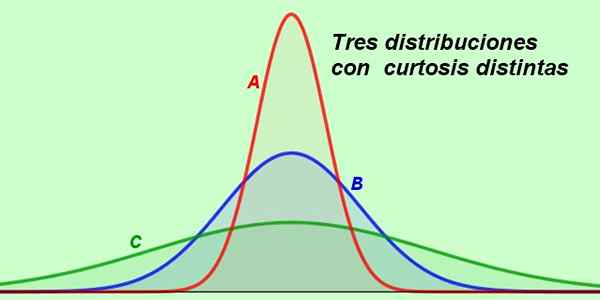
Załóżmy, że poniższy wykres pokazuje rozkłady wynagrodzenia 3 działów tej samej firmy:

Rysunek 2. Trzy różne rozkłady ilustrują praktyczne sytuacje. (Przygotowane przez Fanny Zapata)

Krzywa A jest najbardziej smukła ze wszystkich, a w swojej formie wywnioskowano, że większość wynagrodzeń tego działu jest bardzo zbliżona do średniej, dlatego większość pracowników otrzymuje podobną rekompensatę.

Może ci służyć: liczby całkowitym

Ze względu na rolę w dziale B krzywa wynagrodzeń jest zgodna z normalnym rozkładem, ponieważ krzywa jest mezokurka, w której zakładamy, że wynagrodzenia były losowo rozmieszczone.

I wreszcie mamy bardzo spłaszczoną krzywą C, znak, że w tym dziale zasięg wynagrodzeń jest znacznie szerszy niż w innych.

Wyniki egzaminu

Załóżmy teraz, że trzy krzywe na rycinie 2 reprezentują wyniki egzaminu zastosowanego do trzech grup studentów tego samego przedmiotu.

Grupa, której kwalifikacje są reprezentowane przez krzywą do lepokurki, jest dość jednorodna, większość uzyskała średnią lub bliską ocenę.

Możliwe jest również, że wynik był spowodowany faktem, że pytania egzaminacyjne miały mniej więcej taki sam stopień trudności.

Z drugiej strony wyniki grupy C wskazują większą heterogeniczność w grupie, która prawdopodobnie zawiera przeciętnych studentów, niektórych wybitnych studentów i z pewnością kolejna mniej uważna.

Lub może to oznaczać, że pytania testu miały bardzo różne stopnie trudności.

Krzywa B jest mezokurka, co wskazuje, że wyniki testu były zgodne z rozkładem normalnym. Jest to zwykle najczęstszy przypadek.

Rozwiązany przykład ograniczenia

Znajdź współczynnik wskazujący Fishera dla następujących klas, uzyskany na egzaminie fizyki dla grupy uczniów, ze skalą od 1 do 10:

5, 5, 4, 7, 7.7, 9, 8, 9, 4, 3

Rozwiązanie

Poniższe wyrażenie zostanie wykorzystane do danych nieogrupowanych, podane w poprzednich sekcjach:

Ze współczynnikiem punktu Fishera podanego przez:

Może ci służyć: tożsamości pitagorejskie: demonstracja, przykład, ćwiczenia

K = g₂ - 3

Ta wartość pozwala poznać rodzaj rozkładu.

Aby obliczyć g₂ Jest to wygodne w uporządkowanym sposób, krok po kroku, ponieważ należy rozwiązać kilka operacji arytmetycznych.

Krok 1

Po pierwsze, obliczana jest średnia kwalifikacji. Istnieje n = 11 danych.

X = (5+5+4+7+7+7+9+8+9+4+3)/11 = 6.182

Krok 2

Znaleziono odchylenie standardowe, dla którego stosuje się to równanie:

 Za pomocą kalkulatora z funkcjami statystycznymi wynik jest natychmiastowy:

σ = 1.992

Lub możesz również zbudować tabelę, która jest również wymagana do następnego kroku i w którym potrzebny jest każdy termin podsumowania, począwszy od (x_Siema - X), zatem (x_Siema - X)² A potem (x_Siema - X)⁴ :

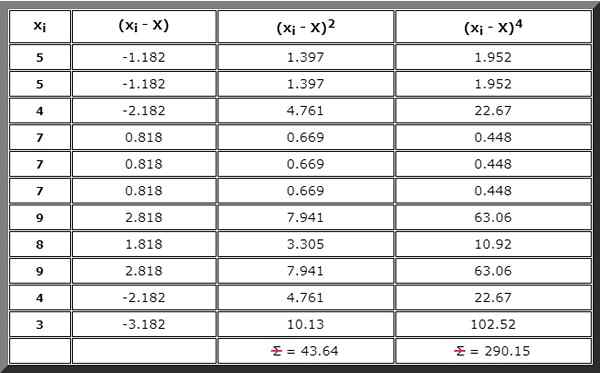
Krok 3

Wykonaj sumę wskazaną w liczniku formuły dla g₂. W tym celu stosuje się wynik prawej kolumny poprzedniej tabeli:

(X_Siema - X)⁴= 290.piętnaście

Dlatego:

G₂ = (1/11) x 290.15/1.992⁴ = 1.675

Współczynnik oznakowania Fishera jest:

K = g₂ - 3 = 1.675 - 3 = -1.325

Jakie interesy są znakiem wyniku, który, gdy ujemny, odpowiada frazesie różnych poziomów trudności.

Użycie arkusza kalkulacyjnego, takiego jak Excel, znacznie ułatwia rozdzielczość tego rodzaju problemów, a także oferuje opcję wykresu dystrybucji.

Bibliografia

1. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
2. Marco, f. Zmiana. Odzyskane z: ekonomipedia.com.
3. Oliva, J. Asymetria i ograniczenie. Pobrano z: StatisticSaucv.Akta.WordPress.com.
4. Spurr, w. 1982. Podejmowanie decyzji w administracji. Limusa.
5. Wikipedia. Kurtoza. Źródło: w:.Wikipedia.org.