Jaki jest zasięg statystyczny? (Z przykładami)

On zakres, Wycieczka lub amplituda w statystykach jest różnica (odejmowanie) między maksymalną wartością a minimalną wartością zestawu danych z próbki lub populacji. Jeśli zakres z literą R i dane jest reprezentowane za pomocą X, Formuła zakresu jest po prostu:

R = x_Max - X_min

 Gdzie x_Max Jest to maksymalna wartość danych i x_min To jest minimum.

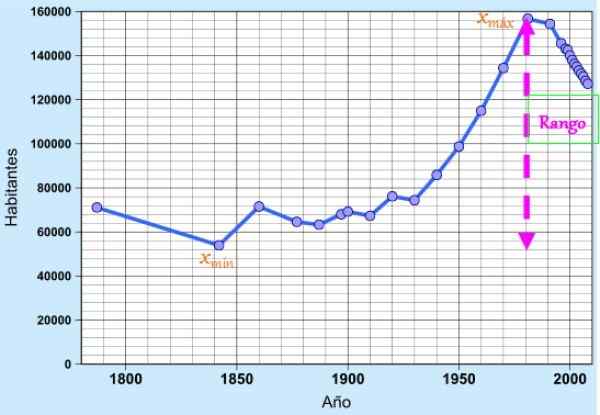
Rysunek 1. Zakres danych odpowiadających populacji Cádiz w ciągu ostatnich dwóch wieków. Źródło: Wikimedia Commons.

Koncepcja jest bardzo przydatna jako prosta miara dyspersji, aby szybko docenić zmienność danych, ponieważ wskazuje na wydłużenie lub długość przedziału, w którym są one znalezione.

Załóżmy na przykład pozycję grupy 25 studentów pierwszego roku inżynierii na uniwersytecie. Najwyższy uczeń w grupie mierzy 1.93 m i najniższy 1.67 m. Są to ekstremalne wartości danych przykładowych, dlatego ich droga to:

R = 1.93 - 1.67 m = 0.26 m lub 26 cm.

Postawa studentów tej grupy jest rozmieszczona w tym zakresie.

[TOC]

Zalety i wady

Zakres jest, jak powiedzieliśmy wcześniej, miara rozproszonych danych. Mały zakres wskazuje, że dane są mniej lub bardziej bliskie, a dyspersja jest niewielka. Z drugiej strony większy zakres wskazuje, że dane są bardziej rozproszone.

Zalety obliczania zakresu są oczywiste: jest to bardzo proste i szybkie znalezienie, ponieważ jest to prosta różnica.

Ma również te same jednostki, co dane, z którymi działają, a koncepcja jest bardzo łatwa do interpretacji dla każdego obserwatora.

W przykładzie pozycji studentów inżynierii, gdyby zasięg wynosił 5 cm, powiedzielibyśmy, że wszyscy uczniowie są tego samego rozmiaru. Ale w zakresie 26 cm natychmiast zakładamy, że w próbie są studenci wszystkich pośrednie. Czy to założenie zawsze dobrze?

Może ci służyć: różnica między okrągiem a obwodem (z przykładami)

Wady zakresu jako miara dyspersji

Jeśli spojrzymy uważnie, w naszej próbie 25 studentów inżynierii tylko jeden z nich mierzy 1.93 i pozostałe 24 mają bliskie 1.67 m.

A jednak zasięg pozostaje taki sam, chociaż jest całkowicie możliwe, że w przeciwnym razie występuje: wzrost większości oscyluje około 1.90 mi tylko jeden mierzy 1.67 m.

W każdym razie rozkład danych jest bardzo inny.

Wady zakresu jako miary dyspersji wynikają z faktu, że wykorzystuje on tylko ekstremalne wartości i ignoruje wszystkie pozostałe. Ponieważ większość informacji jest utracona, nie ma pojęcia, w jaki sposób dystrybuowane są dane.

Inną ważną cechą jest to, że zakres próbki nigdy się nie zmniejsza. Jeśli dodamy więcej informacji, to znaczy, rozważamy więcej danych, zakres wzrasta lub pozostaje taki sam.

W każdym razie jest to przydatne tylko podczas pracy z małymi próbkami, jego unikalne zastosowanie nie jest zalecane jako miara dyspersji w dużych próbkach.

Należy zrobić uzupełnienie obliczania innych miar dyspersji, które uwzględniają informacje dostarczone przez całkowitą dane: trasa Interkwartyliczny, wariancja, odchylenie standardowe i współczynnik zmienności.

Trasa interkwarialna, kwartyle i rozwiązany przykład

Uświadomiliśmy się, że osłabienie zakresu jako miary dyspersji polega na tym, że wykorzystuje on tylko ekstremalne wartości rozkładu danych, pomijając pozostałych.

Aby uniknąć tych niedogodności, kwartyle: Trzy wartości znane jako miary pozycji.

Rozpowszechniają dane, które nie są zgrupowane na cztery części (inne szeroko stosowane miary pozycji to Decyle i percentyle). To są jego cechy:

-Pierwszy kwartyl q₁ Jest to wartość danych tak, że 25 % wszystkich z nich jest mniej niż q₁.

Może ci służyć: proporcjonalność stała: co to jest, obliczenia, ćwiczenia

-Drugi kwartyl q₂ To jest mediana rozkładu, co oznacza, że ​​połowa (50 %) danych jest mniejsza niż ta wartość.

-Wreszcie trzeci kwartyl q₃ wskazuje, że 75 % danych jest mniej niż q₃.

Następnie zakres międzywartylowy lub trasa międzykwartylowa jest zdefiniowana jako różnica między trzecim kwartylem Q₃ i pierwszy kwartyl q₁ danych:

Podróż interkwarowana = r_Q = Q₃ - Q₁

W ten sposób wartość rangi r_Q Nie mają tak na to wpływu ekstremalne wartości. Dlatego wskazane jest użycie go, jeśli chodzi o stronnicze dystrybucje, takie jak bardzo wysoki lub bardzo niscy studenci opisani powyżej.

- Obliczanie cuarty

Istnieje kilka sposobów ich obliczenia, tutaj zaproponujemy jeden, ale w każdym razie konieczne jest znanie Liczba zamówienia "N_albo”, Które jest miejscem, które zajmuje odpowiedni kwartyl w rozmieszczeniu.

To znaczy, jeśli na przykład termin odpowiadający Q₁ jest drugim, trzecim lub czwartym i tak dalej na dystrybucji.

Pierwszy kwartyl

N_albo (Q₁) = (N+1) / 4

Drugi kwartyl lub mediana

N_albo (Q₂) = (N+1) / 2

Trzeci kwartyl

N_albo (Q₃) = 3 (n+1) / 4

Gdzie n jest numerem danych.

Mediana to wartość, która jest odpowiednia w trakcie rozkładu. Jeśli numer danych jest dziwny, nie ma problemu z ich znalezieniem, ale jeśli jest nawet, to dwie wartości centralne są uśredniane, aby zamienić je w jeden.

Po obliczeniu numeru zamówienia po jednej z tych trzech zasad:

-Jeśli nie masz dziesiętnych, poszukiwane są dane wskazane w dystrybucji i będzie to czwarte przeszukane.

-Gdy numer zamówienia jest w połowie dwóch, wówczas dane wskazane przez całą część z następującym faktem są uśredniane, a wynik jest odpowiedni kwartyl.

-W każdym innym przypadku najbliższa liczba całkowita jest zaokrąglona, ​​a to będzie czwarte miejsce.

Może ci służyć: zasada addytywna

Rozwiązany przykład

W skali od 0 do 20 grupy 16 studentów matematyki uzyskałem następujące oceny (punkty) na częściowym egzaminie:

16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14

Znajdować:

a) Data lub droga danych.

b) Wartości kwartyli q₁ i Q₃

c) Zakres interkwarilu.

Rysunek 2. Czy kwalifikacje tego egzaminu matematycznego wykonują tak dużą zmienność? Źródło: Pixabay.

Rozwiązanie

Pierwszą rzeczą, aby znaleźć trasę, jest zamówienie lub zmniejszenie danych. Na przykład w rosnącej kolejności:

1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20

Przez wzór podany na początku: r = x_Max - X_min

R = 20 - 1 punkty = 19 punktów.

Według wyniku oceny te mają wielką dyspersję.

Rozwiązanie b

N = 16

N_albo (Q₁) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4.25

Jest to liczba z dziesiętną, której cała część to 4. Następnie przechodzimy do dystrybucji, poszukiwane są dane, które zajmują czwarte miejsce, a ich wartość jest uśredniona z wartością piątej pozycji. Ponieważ oba są 9, średnia wynosi również 9, a następnie:

Q₁ = 9

Teraz powtarzamy procedurę, aby znaleźć Q₃:

N_albo (Q₃) = 3 (n +1) / 4 = 3 (16 +1) / 4 = 12.75

Znowu jest to dziesiętne, ale ponieważ nie jest w połowie drogi do 13. Poszukiwany kwartyl zajmuje trzynaście pozycji i jest:

Q₃ = 16

Rozwiązanie c

R_Q = Q₃ - Q₁ = 16 - 9 = 7 punktów.

Że, jak widzimy, jest znacznie mniejsze niż zakres danych obliczony w sekcji A), ponieważ minimalna ocena wynosiła 1 punkt, wartość znacznie dalej od pozostałych.

Bibliografia

1. Berenson, m. 1985. Statystyka administracji i ekonomii. Inter -American s.DO.
2. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
3. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
4. Przykłady kwartyli. Źródło: Mathematics10.internet.
5. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
6. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.