Formuła i równania quasENTive, przykłady, ćwiczenia

 Quasive Disquaise, quasi wariancja lub niezdrowa wariancja jest statystyczną miarą rozproszenia danych próbka Dotyczące średniej. Próbka z kolei składa się z serii danych pobranych z głównego wszechświata, zwanego populacja.

Jest oznaczony na kilka sposobów, tutaj został wybrany S_C² I aby to obliczyć, następuje następujący formuła:

Rysunek 1. Definicja quasetywności. Źródło: f. Zapata.

Gdzie:

-S_C ² = Quasirance lub wariancja próbki (wariancja próbki)

-X_Siema = Każdy z przykładowych danych

-N = liczba obserwacji

-X = Średnia próbki

Ponieważ jedność próbki quasENTIENTIVES jest kwadratem jednostki, w której przychodzi próbka, w momencie interpretacji wyników preferowanych jest współpraca z quasi odchylenie standardowe lub standardowe odchylenie próbki.

To jest oznaczone jako S_C I jest uzyskiwany przez wyodrębnienie pierwiastka kwadratowego kwasiwaryczności:

S_C = √ s_C ²

Quasirance jest podobny do wariancji S², z jedyną różnicą, że w mianowniku jest N-1, podczas gdy w wariancji jest to podzielone tylko przez N. Oczywiste jest, że gdy n jest bardzo duże, wartości obu są takie same.

Kiedy wartość quasirance jest znana, możesz od razu wiedzieć, że o wariancji.

[TOC]

Przykłady quasivelity

Chcesz poznać cechy dowolnej populacji: ludzi, zwierząt, roślin i ogólnie rzeczników. Ale analiza całej populacji może nie być łatwym zadaniem, zwłaszcza jeśli liczba elementów jest bardzo duża.

Następnie pobierane są próbki, z nadzieją, że ich zachowanie odzwierciedla zachowanie populacji, a tym samym być w stanie wyciągnąć wnioski na ten temat, dzięki temu, które zasoby są zoptymalizowane. To jest znane jako wnioskowanie statystyczne.

Oto kilka przykładów, w których quasirance i quasi odchylenie standardowe związane z quasi służą jako wskaźnik statystyczny, wskazując, że wyniki uzyskane w odniesieniu do średniej.

Może ci służyć: obwód krąg: jak go wybrać i formuły, rozwiązane ćwiczenia

1.- Dyrektor marketingu firmy, która produkuje akumulatory samochodowe, musi oszacować, w miesiącach średni czas trwania baterii.

Aby to zrobić, losowo wybierz próbkę 100 baterii tej marki zakupionej. Firma zachowuje zapis danych kupujących i może przeprowadzić ich wywiad, aby poznać czas trwania baterii.

Rysunek 2. Cuasive ocena jest przydatna do dokonywania wniosków i kontroli jakości. Źródło: Pixabay.

2.- Kierownictwo akademickie instytucji uniwersyteckiej musi oszacować rejestrację następnego roku, analizując liczbę studentów, którzy mają zatwierdzać obecnie przedmiotów.

Na przykład z każdej z sekcji, które obecnie badają fizyczny podmiot I, adres może wybrać próbkę studentów i przeanalizować jej wyniki na wspomnianym krześle. W ten sposób możesz wywnioskować, ilu studentów będzie studiować fizykę II w następnym okresie.

3.- Grupa astronomów skupia swoją uwagę na części nieba, w której obserwowana jest pewna liczba gwiazd o pewnych cechach: na przykład wielkość, masa i temperatura.

Warto zapytać, czy gwiazdy w innym podobnym regionie będą miały te same cechy, w tym gwiazdy w innych galaktykach, takie jak sąsiednie chmury Magallanes lub Andromeda.

Po co dzielić między N-1?

W quasirance jest on podzielony między N-1 zamiast N I dzieje się tak, ponieważ quasirance to Nalegał estymator, Jak stwierdzono na początku.

Zdarza się, że z tej samej populacji możliwe jest wydobycie wielu próbek. Wariancja każdej z tych próbek może być również uśredniona, ale średnia z tych wariancji nie okazuje się równa wariancji populacji.

Może ci służyć: wartość względna

W rzeczywistości średnia wariancji próbki ma tendencję do nie docenia N-1 W mianowniku. Można zweryfikować, że wartość oczekiwana o quasresywności e (s_C²) jest dokładnie².

Dlatego mówi się, że quasirance jest insensted i jest lepszym estymatorem wariancji populacji².

Alternatywny sposób obliczenia Quasive Disquaise

Łatwo wykazuje, że quasirance można również obliczyć w następujący sposób:

S_C² = [∑x² / (N -1)] - [∑nx² / (N-1)]

Standardowy wynik

Mając odchylenie od próbki, możemy wiedzieć, ile odchyleń standardowych ma określoną wartość x, powyżej lub poniżej średniej.

W tym celu stosuje się następujące wyrażenie bezwymiarowe:

Standardowy wynik = (x - x) / s_C

Ćwiczenie rozwiązane

Oblicz quasirance i quasi -typowe odchylenie następujących danych, które składają się z miesięcznych płatności w $ dokonanych przez firmę ubezpieczeniową na prywatną klinikę.

863 903 957 1041 1138 1204 1354 1624 1698 1745 1802 1883

a) Użyj definicji quasachowości podanej na początku, a także zweryfikuj wynik według alternatywnej formy podanej w poprzednim rozdziale.

b) Oblicz standardowy wynik drugiego danych, odczytu od góry do dołu.

Rozwiązanie

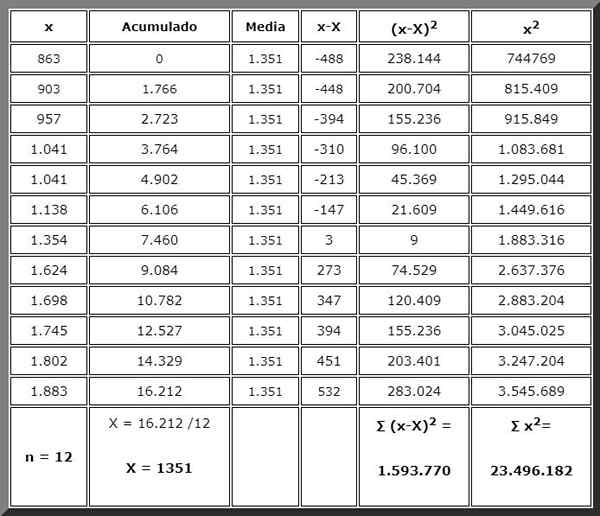
Problem można rozwiązać ręcznie za pomocą prostego lub naukowego kalkulatora, dla którego musimy postępować w porządku. A dla tego nic lepszego niż uporządkowanie danych w tabeli takiej jak pokazano poniżej:

Dzięki tabeli zorganizowałeś informacje, a kwoty, które będą potrzebne w formułach, znajdują się na końcu odpowiednich kolumn, gotowe do użycia natychmiast. Podsumowania są wskazane odważne.

Może ci służyć: jakie są 7 elementów obwodu?

Przeciętna kolumna jest zawsze powtarzana, ale warto, ponieważ wygodnie jest mieć wartość w widoku, aby wypełnić każdy wiersz tabeli.

Wreszcie, stosowane jest równanie quasirance podawane na początku, tylko wartości są zastąpione i pod względem sumy już go obliczyliśmy:

S_C² = 1.593.770 / (12-1) = 1.593.770 /11 = 144.888.2

Jest to wartość Quasirance, a jej jednostki to „dolary kwadratowe”, co nie ma większego sensu praktycznego, więc obliczane są standardowe quasides próbki, co jest niczym więcej niż pierwiastkiem kwadratowym Quasivarian:

S_C = (√144.888,2) $ = 380,64 $

Natychmiast potwierdza się, że wartość ta jest również uzyskiwana z alternatywną formą kwasiwaryczności. Niezbędna suma znajduje się na końcu ostatniej kolumny po lewej:

S_C² = [∑x² / (N-) - [∑nx² / (N-1)] = [23.496.182/11] - [12 x 1351²/ Eleven]

= 2.136.016.55 - 1.991.128,36 = 144.888 USD kwadratowe

Jest to ta sama wartość uzyskana w przypadku wzoru podanego na początku.

Rozwiązanie b

Druga wartość od góry do dołu to 903, jego standardowy wynik to

Standardowy wynik 903 = (x - x) / s_C = (903 - 1351)/380.64 = -1.177

Bibliografia

1. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
2. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
3. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
4. Miary dyspersji. Odzyskane z: Thales.Cica.Jest.
5. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.