Miary centralnej tendencji do zgrupowanych formuł danych, ćwiczenia

Miary trendu centralny Wskazują wartość, wokół której są dane rozkładu. Najbardziej znany jest średnia lub średnia arytmetyczna, która polega na dodaniu wszystkich wartości i podzieleniu wyniku przez całkowitą liczbę danych.

Jeśli jednak rozkład składa się z dużej liczby wartości i nie jest prezentowany w uporządkowany sposób, nie jest łatwo wykonać niezbędne obliczenia w celu wyodrębnienia cennych zawartych informacji.

Rysunek 1. Centralne miary tendencji dla zgrupowanych danych są dobrym wskazaniem ogólnego zachowania danych

Dlatego są pogrupowani na zajęcia lub kategorie, aby opracować dystrybucja Częstotliwości. Wykonując poprzednią kolejność danych, w tym łatwiej obliczyć środkowe miary tendencji, w tym:

-Połowa

-Mediana

-Moda

-Średnia geometryczna

-Średnia harmoniczna

Formuły

Poniżej mamy wzory centralnych miar tendencji dla zgrupowanych danych:

Średnia arytmetyczna

Średnia jest najczęściej używana do scharakteryzowania danych ilościowych (wartości numeryczne), chociaż jest dość wrażliwa na ekstremalne wartości rozkładu. Jest obliczany przez:

Z:

-X: Średnia lub średnia arytmetyka

-F_Siema: Częstotliwość klasy

-M_Siema: Marka klasowa

-G: Numer zajęć

-N: Całkowite dane

Mediana

Aby to obliczyć, konieczne jest znalezienie interwału zawierającego obserwację N/2 i międzypolarne w celu ustalenia wartości numerycznej wspomnianej obserwacji za pomocą następującego wzoru:

Gdzie:

-C: szerokość interwałów, do której należy mediana

-B_M: dolna granica wspomnianego przedziału

-F_M: Liczba obserwacji zawartych w przedziale

-N/2: Całkowite dane podzielone przez 2.

-F_BM: liczba obserwacji przed przerwą zawierającą medianę.

Dlatego mediana jest miarą pozycji, to znaczy dzielą zestaw danych na dwie części. Można je również zdefiniować kwartyle, Decyle I percentyle, który dzieli rozkład na odpowiednio cztery, dziesięć i sto części.

Może ci służyć: Fourier Transform: właściwości, aplikacje, przykłady

Moda

W zgrupowanych danych poszukiwana jest klasa lub kategoria zawierająca większość obserwacji. To jest Klasa modalna. Rozkład może mieć dwie lub więcej mody, w którym to przypadku się nazywa Bimodal I Multimodal, odpowiednio.

Możesz także obliczyć modę w zgrupowanych danych po równaniu:

Z:

-L₁: Dolna granica klasy, w której jest moda

-Δ₁: Pozostaje między częstotliwością klasy modalnej a częstotliwością poprzedzającej ją.

-Δ₂: Odejmij między częstotliwością klasy modalnej a częstotliwością podążającej za nią klasy.

-C: Szerokość interwałowa zawierająca modę

Średnia harmoniczna

Średnia harmoniczna jest oznaczona przez H. Kiedy masz zestaw N Wartości x₁, X₂, X₃… Harmonijną średnią jest odwrotność lub wzajemna średnia arytmetyczna odwrotności wartości.

Łatwiej jest zobaczyć to przez formułę:

A podczas zgrupowanych danych wyrażenie jest przekształcone w:

Gdzie:

-H: średnia harmoniczna

-F_Siema: Częstotliwość klasy

-M_Siema: Marka klasowa

-G: Numer zajęć

-N = f₁ + F₂ + F₃ +..

Średnia geometryczna

Jeśli masz N Liczby dodatnie x₁, X₂, X₃… Jego średnia geometryczna jest obliczana przez N-em iloczynu wszystkich liczb:

W przypadku zgrupowanych danych można wykazać, że logarytm dziesiętny geometrycznego logu G jest podany przez:

Gdzie:

-G: Średnia geometryczna

-F_Siema: Częstotliwość klasy

-M_Siema: Marka klasowa

-G: Numer zajęć

-N = f₁ + F₂ + F₃ +..

Związek między H, G i x

Zawsze prawdą jest:

H ≤ g ≤ x

Najczęściej używane definicje

Konieczne są następujące definicje, aby znaleźć wartości opisane w poprzednich formułach:

Częstotliwość

Częstotliwość jest definiowana jako liczba powtarzanych faktów.

Zakres

Jest to różnica między wartością główną a niewielką, obecną w rozkładu.

Liczba klas

Aby wiedzieć, ile klas grupujemy dane, używamy niektórych kryteriów, na przykład następujące:

Może ci służyć: 17 uzasadnionych problemów

Granice

Wywołują ekstremalne wartości każdej klasy lub przedziału granice i każda klasa może mieć oba dobrze zdefiniowane limity, w którym to przypadku ma dolną granicę, a jedną większą. Lub może mieć otwarte limity, gdy podano zakres, na przykład wartości większe lub niższe niż określona liczba.

Marka klasowa

Po prostu składa się z punktu środkowego przedziału i jest obliczane uśredniające górną granicę i dolną granicę.

Szerokość przedziału

Dane można pogrupować w klasy o równej lub różnej wielkości, jest to szerokość lub amplituda. Pierwsza opcja jest najczęściej używana, ponieważ ułatwia obliczenia, chociaż w niektórych przypadkach konieczne jest, aby klasy miały inną szerokość.

Szerokość C Od przedziału można go określić w następującym wzorze:

C = zakres / n_C

Gdzie_C Jest to liczba klas.

Ćwiczenie rozwiązane

Below we have a series of speed measurements in km/h, taken with radar, which correspond to 50 cars that passed through a street in a certain city:

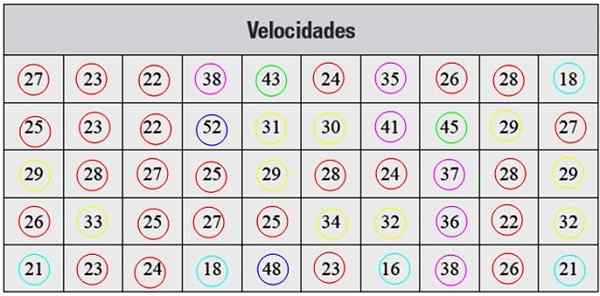Rysunek 2. Tabela do ćwiczenia rozwiązanego. Źródło: f. Zapata.

Rozwiązanie

Przedstawione dane nie są zorganizowane, więc pierwszym krokiem jest zgrupowanie ich na zajęcia.

Kroki w celu pogrupowania danych i zbudowania tabeli

Krok 1

Znajdź zasięg r:

R = (52–16) km/h = 36 km/h

Krok 2

Wybierz liczbę klas n_C, Zgodnie z danymi kryteriami. Ponieważ jest 50 danych, możemy wybrać n_C = 6.

Krok 3

Oblicz szerokość C interwału:

C = zakres /n_C = 36/6 = 6

Krok 4

Klasy formularzy i dane grupy w następujący sposób: Dla pierwszej klasy A dolna granica jest wybierana, gdy tylko niższa wartość obecna w tabeli zostanie dodana do tej wartości C = 6, wcześniej obliczona, a zatem uzyskuje górną granicę limitu pierwsza klasa.

Przechodzi w ten sam sposób, aby zbudować resztę klas, jak pokazano w poniższej tabeli:

Może ci służyć: jaki jest numer Capicúa? Właściwości i przykłady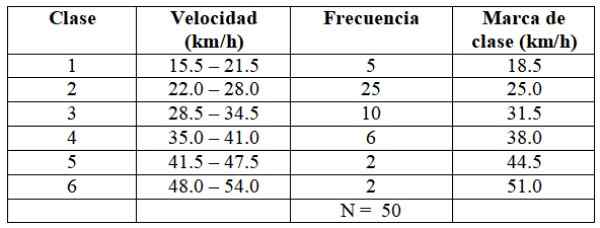

Każda częstotliwość odpowiada koloru na ryc. 2, w ten sposób zapewnia, że ​​nie ma wartości, aby nie uwzględnić.

Średnie obliczenia

X = (5 x 18.5 +25 x 25.0 + 10 x 31.5 + 6 x 38.0 + 2 x 44.5 + 2 x 51.0) ÷ 50 = 29.03 km/h

Mediana obliczeń

Mediana znajduje się w klasie 2 tabeli, ponieważ istnieje pierwsze 30 danych dystrybucji.

-Szerokość przedziału, do której należy mediana: C = 6

-Dolna granica przedziału, w którym mediana to: B_M = 22.0 km/h

-Liczba obserwacji zawartych w przedziale f_M = 25

-Całkowite dane podzielone przez 2: 50/2 = 25

-Liczba obserwacji przed przedziałem zawierającym medianę: F_BM = 5

A operacja to:

Mediana = 22.0 + [(25-5) ÷ 25] × 6 = 26.80 km/h

Moda

Moda znajduje się również w klasie 2:

-Szerokość interwału: c = 6

-Dolna granica klasy, w której znajduje się moda: l₁ = 22.0

-Odejmij między częstotliwością klasy modalnej a częstotliwością poprzedzającej ją₁ = 25-5 = 20

-Odejmij między częstotliwością klasy modalnej a częstotliwością następnej klasy: δ₂ = 25 - 10 = 15

Z tymi danymi operacja wynosi:

Moda = 22.0 + [20 ÷ (20 + 15)] x6 = 25.4 km/h

Obliczanie średniej geometrycznej

N = f₁ + F₂ + F₃ +... = 50

log g = (5 x log 18.5 + 25 x dziennik 25 + 10 x dziennik 31.5 + 6 x dziennik 38 + 2 × log 44.5 + 2 x log 51) /50 =

log g = 1.44916053

G = 28.13 km/h

Średnia harmoniczna obliczenie

1/h = (1/50) x [(5/18.5) + (25/25) + (10/31.5) + (6/38) + (2/44.5) + (2/51)] = 0.0366

H = 27.32 km/h

Podsumowanie środków tendencji centralnych

Jednostki zmienne to km/h:

-Media: 29.03

-Mediana: 26.80

-Moda: 25.40

-Media geometryczne: 28.13

-Średnia harmoniczna: 27.32

Bibliografia

1. Berenson, m. 1985. Statystyka administracji i ekonomii. Inter -American s.DO.
2. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
3. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
4. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
5. Spiegel, m. 2009. Statystyka. Seria Schaum. 4 Ta. Wydanie. McGraw Hill.
6. Leczenie zgrupowanych danych. Odzyskane z: Itchihuahua.Edu.MX.
7. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.