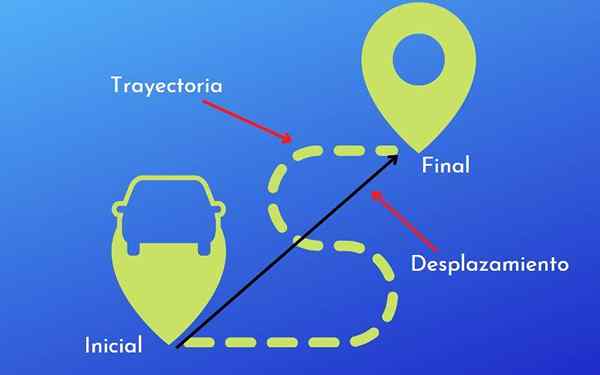
Trajektoria i przemieszczenie

Różnica między trajektorią a przemieszczeniem. Z licencją

Różnica między trajektorią a przemieszczeniem jest to, że ta ostatnia jest odległością i kierunkiem przechodzącym obiektem, podczas gdy trajektoria jest trasą lub formą przyjętą przez ruch tego obiektu.

Jednak, aby wyraźniej zobaczyć różnice między przemieszczeniem a trajektorią, lepiej wyjaśnić przykłady, które umożliwiają lepsze zrozumienie obu terminów.

Przemieszczenie

Jest to rozumiane jako odległość i kierunek przemieszczane przez obiekt, biorąc pod uwagę jego początkową pozycję i końcową pozycję, zawsze w linii prostej. Do jego obliczeń, ponieważ jest to wielkość wektora, stosowane są pomiary długości znane jako centymetry, mierniki lub kilometry.

Wzór obliczania przemieszczenia jest zdefiniowany w następujący sposób:

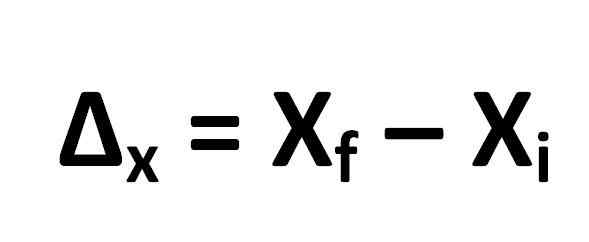
Z którego następuje:

- Δ_X = przemieszczenie

- X_F = końcowa pozycja obiektu

- X_Siema = początkowa pozycja obiektu

Przykład przemieszczenia

1. Jeśli grupa dzieci jest na początku trasy, której początkowa pozycja wynosi 50 m, porusza się w linii prostej, określając przemieszczenie w każdym z punktów x_F. 

- X_F = 120 m

- X_F = 90 m

- X_F = 60 m

- X_F = 40 m

2. Dane problemowe są wyodrębnione przez zastąpienie wartości x₂ i x₁ W formule przemieszczenia:

- Δ_X = ?

- X_Siema = 50 m

- Δ_X = X_F - X_Siema

- Δ_X = 120 m - 50 m = 70 m

3. W tym pierwszym podejściu mówimy, że δ_X Jest to równe 120 m, co odpowiada pierwszej wartości, którą znajdujemy od x_F, mniej 50 m, co jest wartością x_Siema, Powoduje 70 m, to znaczy po osiągnięciu 120 m przemieszczenia przemieszczenie wynosiło 70 m po prawej stronie.

Może ci służyć: oddział laboratoryjny

4. Rozwiązujemy w ten sam sposób dla wartości B, C i D

- Δ_X = 90 m - 50 m = 40 m

- Δ_X = 60 m - 50 m = 10 m

- Δ_X = 40 m - 50 m = - 10 m

W tym przypadku przesunięcie dało nam negatywne, oznacza to, że pozycja końcowa znajduje się w przeciwnym kierunku początkowej pozycji.

Trajektoria

Jest to trasa lub linia określona przez obiekt podczas jego ruchu i oceny w systemie międzynarodowym, ogólnie przyjmuje kształty geometryczne, takie jak linia, przypowieść, koło lub elipsa.

Jest to identyfikowane za pomocą wyimaginowanej linii i jako ilość skalarna jest mierzona w metrach.

Należy zauważyć, że aby obliczyć trajektorię, musimy wiedzieć, czy ciało jest w spoczynku lub poruszaniu się, to znaczy jest przesłane do systemu referencyjnego, który wybieramy.

Równanie do obliczenia trajektorii obiektu w systemie międzynarodowym jest podane przez:

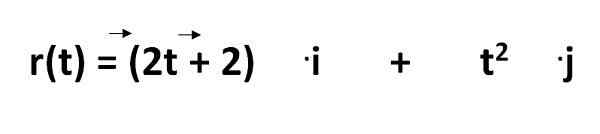
Z których musimy:

- R (t) = jest to równanie trajektorii

- 2T - 2 i T² = reprezentuj współrzędne jako funkcję czasu

-  ^.ja i ^.J = to wektory jednostkowe

Aby zrozumieć obliczenie trajektorii przeżywanej przez obiekt, opracujemy następujący przykład:

Oblicz równanie trajektorii następujących wektorów pozycji:

- R (t) = (2T + 7) ^.I + t^{2 .}J

- R (t) = (t - 2) ^.R&D 2T ^.J

Pierwszy krok: jako równanie trajektorii jest funkcją x, aby zdefiniować wartości odpowiednio x i y w każdym z podniesionych wektorów:

1. Rozwiąż pierwszą pozycję wektora:

- R (t) = (2T + 7) ^.I + t^{2 .}J

2. Ty = f (x), gdzie x jest podawany przez zawartość wektora jednostki ^.I e i jest podawane przez zawartość wektora jednostki ^.J:

Może ci służyć: ad hoc: pochodzenie terminu, znaczenia i przykłady użytkowania

- X = 2t + 7

- Y = t²

3. y = f (x), to znaczy czas nie jest częścią wyrażenia, dlatego musimy to wyczyścić, mamy:

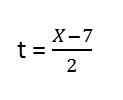
4. Wymieniamy prześwit w i. Gorset:

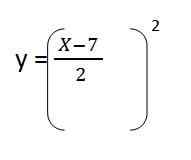
5. Rozwiązujemy zawartość nawiasu i mamy równanie powstałej trajektorii dla pierwszego wektora jednostki:

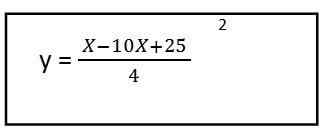
Jak widzimy, spowodowało to równanie drugiego stopnia, oznacza to, że trajektoria dotyczy kształtu paraboli.

Drugi krok: postępujemy w ten sam sposób do obliczania trajektorii wektora drugiego jednostki:

1. R (t) = (t - 2) ^.R&D 2T ^.J

- X = t - 2

- Y = 2t

2. Zgodnie z krokami, które widzieliśmy wcześniej y = f (x), musimy usunąć czas, ponieważ nie jest to część wyrażenia, mamy:

- t = x + 2

3. Zastępujemy prześwit i pozostaniemy:

- y = 2 (x + 2)

4. Rozwiązując nawias, mamy równanie powstałej trajektorii dla wektora drugiego jednostki:

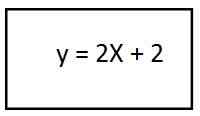
W tej procedurze doprowadziliśmy do linii, która mówi nam, że trajektoria ma postać prostoliniową.

Zrozumiała pojęcia przemieszczenia i trajektorii, możemy wywnioskować resztę różnic między obiema terminami.

Większe różnice między przemieszczeniem a trajektorią

Przemieszczenie

- Jest to odległość i kierunek przejechany przez obiekt, biorąc pod uwagę jego początkową pozycję i końcową pozycję.

- Zawsze zdarza się w linii prostej.

- Jest rozpoznawany za pomocą strzałki.

- Zastosuj miary długości (centymetr, miernik, kilometr).

- Jest to kwota wektorowa.

- Weź pod uwagę kierowany kierunek (prawy lub po lewej)

- Nie bierze pod uwagę czasu spędzonego podczas trasy.

Może ci służyć: kondensacja: koncepcja, proces, przykłady

- Nie zależy to od systemu referencyjnego.

- Gdy punkt początkowy jest tym samym punktem początkowym, przemieszczenie wynosi zero.

- Moduł musi zbiegać się z przestrzenią, aby je koncertować, dopóki trajektoria jest linią prostą i nie ma żadnych zmian w sensie podążania.

- Moduł ma tendencję do wzrostu lub zmniejszania się w miarę wystąpienia ruchu, biorąc pod uwagę trajektorię.

Trajektoria

Jest to trasa lub linia określona przez obiekt podczas jego ruchu. Przyjmuj kształty geometryczne (proste, paraboliczne, okrągłe lub eliptyczne).

- Jest reprezentowany przez wyimaginowaną linię.

- Jest mierzony w metrach.

- Jest to wielkość skalarna.

- Nie bierze pod uwagę sposobu podróżowania.

- Rozważ czas spędzony podczas trasy.

- To zależy od systemu referencyjnego.

- Gdy punkt początkowy lub pozycja początkowa jest taka sama jak pozycja końcowa, trajektoria jest podawana przez przebytą odległość.

- Wartość trajektorii pokrywa się z modułem przemieszczenia wektora, jeśli wynikowa trajektoria jest linią prostą, ale nie ma zmian w sensie do podążania.

- Zawsze rośnie, gdy ciało się porusza, niezależnie od trajektorii.

Bibliografia

1. Fernández, m., Fidalgo, J. (2016). Fizyka i chemia 1. maturka. Paraninfo Editions, S.DO. Hiszpania.
2. Gwatemalski Institute of Radio Education (2011) Fundamental Physics. Grupa Zaculeu w pierwszym semestrze. Gwatemala.