Twierdzenie varignon

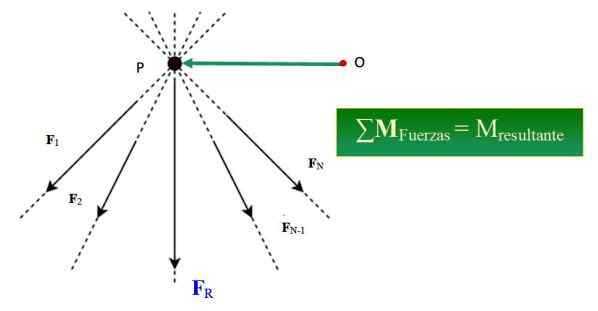
Rysunek 1.- Twierdzenie Varignona potwierdza, że ​​suma momentu sił wokół określonego punktu jest równoważna czasowi wyniku w odniesieniu do tego punktu. Źródło: Wikimedia Commons/F. Zapata.

Jakie jest twierdzenie Varignona?

Twierdzenie Varignona w mechanice stwierdza, że ​​suma momentów wytwarzanych przez układ sił równoczesnych w odniesieniu do określonego punktu jest równa momentowi powstałej siły w odniesieniu do tego samego punktu.

Z tego powodu to twierdzenie to jest również znane jako Początek chwil.

Podczas gdy pierwszym, który stwierdził, był Holender Simon Stevin (1548-1620), twórca paradoksu hydrostatycznego, francuski matematyk Pierre Varignon (1654-1722) był tym, który następnie dał mu swoją ostateczną formę.

Przykład tego, jak działa twierdzenie Varignona w mechanice: Załóżmy, że prosty system dwóch coplanares i równoczesnych sił działa w danym punkcie F₁ I F₂, (Oznaczone odważnym dla swojego wektora). Siły te powodują powstanie siły netto lub wynikającej z tego F_R.

Każda siła wywiera moment obrotowy lub moment w stosunku do punktu lub, który jest obliczany przez produkt wektorowy między wektorem pozycji R_Op i Strengh F, Gdzie R_Op Jest skierowany od lub do punktu zbieżności p:

M_O1 = R_Op × F₁

M_O2 = R_Op × F₂

Biorąc pod uwagę F_R = F₁ + F₂, Więc:

M_ALBO = R_Op × F₁ + R_Op × F₂ = M_O1 + M_O2

Ale jak R_Op Jest to zatem powszechny czynnik stosowania właściwości dystrybucyjnej do produktu krzyżowego:

M_ALBO = R_Op × (F₁ + F₂) = R_Op × F_R                

Dlatego suma momentów lub momentów każdej siły w odniesieniu do punktu lub jest równoważna czasowi powstałej siły w odniesieniu do tego samego punktu.

Oświadczenie i demonstracja

Być systemem n równoległych sił, utworzonych przez F₁, F₂, F₃.. F_N, którego linie działania są przeznaczone w punkcie P (patrz ryc. 1), moment tego systemu siły M_ALBO, Dotyczące punktu lub jest podane przez:

Może ci służyć: niestabilna równowaga: koncepcja i przykłady

M_ALBO = R_Op × F₁ + R_Op × F₂ + R_Op × F₃ +.. R_Op × F_N = R_Op × (F₁ + F₂ + F₃ +.. F_N)

Demonstracja

Aby zademonstrować twierdzenie, wykonana jest właściwość dystrybucyjna produktu wektorowego między wektorami.

Być siłami F₁, F₂, F₃.. F_N zastosowane do punktów₁, DO₂, DO₃… DO_N i równolegle w punkcie P. Wynikowy moment tego systemu, w odniesieniu do punktu lub, nazywany M_ALBO, Jest to suma momentów każdej siły, w odniesieniu do tego punktu:

M_ALBO = ∑ R_Oai × F_Siema

Gdzie suma przechodzi od i = 1 do i = n, ponieważ istnieją n siły. Ponieważ są to siły równoczesne, a ponieważ produkt wektorowy między wektorami równoległymi jest zerowy, zdarza się, że:

R_Pai × F_Siema = 0

Z wektorem zerowym oznaczonym jako 0.

Moment jednej z sił dotyczących o, na przykład siły F_Siema zastosowane w_Siema, Jest napisane w ten sposób:

M_słyszałem = R_Oai × F_Siema

Wektor pozycji R_Oai  Można go wyrazić jako sumę pozycji dwóch wektorów:

R_Oai = R_Op + R_Pai

W ten sposób moment w odniesieniu do lub siły F_Siema Jest:

M_słyszałem = (R_Op + R_Pai) × F_Siema = (R_Op × F_Siema) + (R_Pai × F_Siema)

Ale ostatni termin jest zerowy, jak wyjaśniono powyżej, ponieważ R_Pai jest na linii działania F_Siema, W związku z tym:

M_słyszałem = R_Op × F_Siema

Wiedząc, że moment systemu w odniesieniu do punktu lub jest sumą wszystkich indywidualnych momentów każdej siły w odniesieniu do tego punktu:

M_ALBO = ∑ M_słyszałem = ∑ R_Op × F_Siema

Jak R_Op To jest stałe, wychodzi z suma:

M_ALBO = R_Op × (∑ F_Siema)

Ale ∑ F_Siema Jest to po prostu powstała siatka lub siła F_R, Dlatego natychmiast stwierdzono, że:

Może ci służyć: Leyden Butelka: części, operacja, eksperymenty

M_ALBO = R_Op × F_R

Przykład

Twierdzenie Varignona ułatwia obliczenie momentu siły F Jeśli chodzi o punkt lub strukturę pokazaną na rysunku, jeśli siła jest podzielona na jego prostokątne składniki i obliczany jest moment każdego z nich:

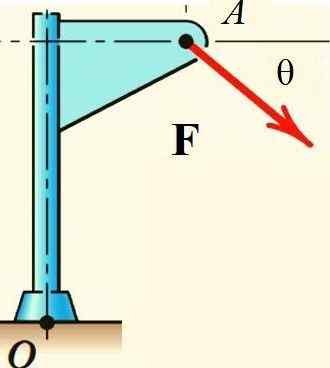Rysunek 2.- Twierdzenie Varignona dotyczy obliczenia momentu siły wokół lub. Źródło: f. Zapata.

Zastosowania twierdzenia varignon

Gdy znana jest siła wynikająca z systemu, twierdzenie Varignona można zastosować w celu zastąpienia suma każdego z momentów wytwarzanych przez siły, które tworzą ją w czasie powstałego.

Jeśli system składa się z sił na tej samej płaszczyźnie i punkcie, w odniesieniu do tego, że chcesz obliczyć moment, który należy do tej płaszczyzny, wynikowy moment jest prostopadły.

Na przykład, jeśli wszystkie siły znajdują się w płaszczyźnie XY, moment jest skierowany na oś Z i pozostaje tylko po to, by znaleźć jej wielkość i znaczenie, tak jest w przypadku przykładu opisanego powyżej.

W takim przypadku twierdzenie Varignona pozwala obliczyć moment wynikający z systemu poprzez podsumowanie. Jest to bardzo przydatne w przypadku systemu trzech sił w wymiarach, dla którego kierunek powstałego momentu nie jest znany a priori.

Aby rozwiązać te ćwiczenia, jest to wygodne.

Ćwiczenie rozwiązane

Według twierdzenia Varignona oblicz moment siły F wokół punktu lub pokazany na rysunku, czy wielkość F wynosi 725 n.

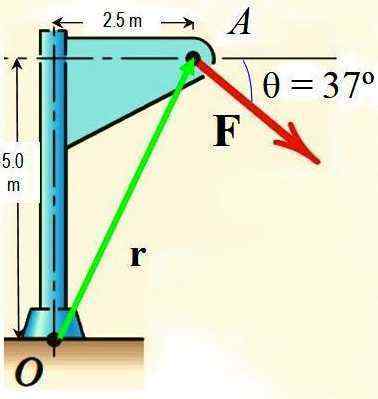Rysunek 3.- Rysunek dla ćwiczenia rozwiązanego. Źródło: f. Zapata.

Rozwiązanie

Aby zastosować twierdzenie Varignona, siła rozkłada się F w dwóch składnikach, których odpowiednie momenty wokół lub są obliczane i dodawane, aby uzyskać wynikowy moment.

Może ci służyć: sztywne ciało

F_X = 725 N ∙ cos 37 º = 579.0 n

F_I = - 725 N n ∙ Sen 37 º = −436.3 n

Podobnie wektor pozycji R skierowane z lub do a ma komponenty:

R_X = 2.5m

R_I = 5.0 m

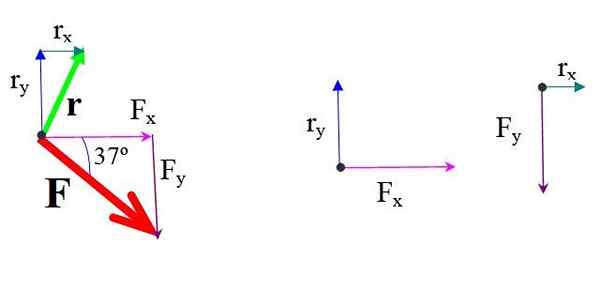Rysunek 4.- Siła i pozycja komponentów. Źródło: f. Zapata.

Moment każdego elementu siły w odniesieniu do lub mnożą siłę i odległość prostopadłą.

Obie siły mają tendencję do obracania struktury w tym samym kierunku, co w tym przypadku jest sensem wyniku, który jest dowolnie przypisany znakiem pozytywnym:

M_Wół = F_X∙ r_I ∙ Sin 90º = 579.0 n ∙ 5.0 m = 2895 n ∙ m

M_Oy = F_I∙ r_X ∙ sin (-90º) = −436.3 N ∙ 2.5 m ∙ (-1) = 1090.8 n ∙ m

Wynikowy moment w odniesieniu do lub jest:

M_ALBO = M_Wół + M_Oy = 3985.8 n ∙ m prostopadle do płaszczyzny i momentu obrotowego.

Bibliografia

1. Bedford, 2000. DO. Mechanika inżynierii: statyczne. Addison Wesley. 
2. Piwo, f. 2010. Statyczny. McGraw Hill. 9na. Wydanie.
3. Hibbeler, R. 1992. Mechanika inżynierów. 6th. Wydanie. Cecsa.
4. HK Engineering. Twierdzenie varignon. Odzyskane z: YouTube.com.
5. Wikipedia. Twierdzenie Varignona (mechanika). Źródło: w:.Wikipedia.org.