Twierdzenie o tym, co polega na aplikacjach i przykładach

On Twierdzenie Thévenin Stwierdza, że ​​obwód z terminalami A i B można zastąpić równoważnym, który składa się ze źródła i oporu szeregowego, którego wartości dają taką samą różnicę potencjału między A i B i tę samą impedancję jak oryginalny obwód.

Twierdzenie to zostało wydane w 1883 roku przez francuskiego inżyniera Léona Charlesa Thévenina, ale twierdzi się, że został napisany trzydzieści lat wcześniej przez niemieckiego fizyka Hermanna von Helmholtza.

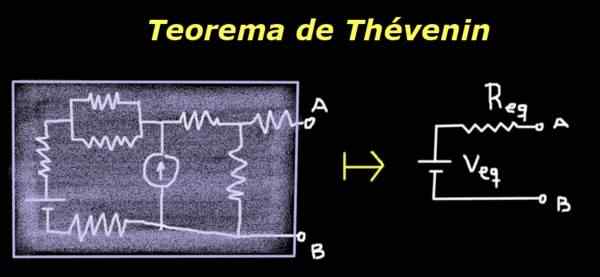
Rysunek 1. Twierdzenie Thévenin. Źródło: Self Made

Jego przydatność polega na tym, że nawet jeśli oryginalny obwód jest złożony lub nieznany, do celów obciążenia lub impedancji umieszczonej między zaciskami A i B, prosty równoważny obwód Thévenin zachowuje się w taki sam sposób, jak oryginalny.

[TOC]

Jak obliczane jest równoważne napięcie po kroku?

Napięcie lub różnica potencjału obwodu równoważnego można uzyskać na następujące sposoby:

- Doświadczalnie

Uzyskanie równoważnego napięcia théveniny

Jeśli jest to urządzenie lub sprzęt w „czarnej skrzynce”, mierzona jest różnica potencjałów między zaciskami A i B z woltomierzem lub oscyloskopem. Bardzo ważne jest, aby nie umieścić obciążenia ani impedancji między zaciskami A i B. 

Woltomierz lub oscyloskop nie reprezentuje żadnego obciążenia dla zacisków, ponieważ obie drużyny mają bardzo dużą (idealnie nieskończoną) impedancję i byłyby tak, jakby terminale A i B były bez obciążenia. Napięcie lub napięcie uzyskane w ten sposób jest równoważne napięcie théveniny.

Uzyskanie równoważnej impedancji théveniny

Aby uzyskać równoważną impedancję z pomiaru eksperymentalnego, umieszcza się rezystancję między zaciskami A i B, a mierzony spadek napięcia lub sygnał napięcia z oscyloskopem. 

Od spadku napięcia w rezystancji znanej wśród zacisków, prąd, który przez niego krąży. 

Produkt prądu uzyskanego z równoważną rezystancją plus zmierzony spadek napięcia w znanej rezystancji jest równy równoważnego napięcia théveniny uzyskanej. Z tej równości wyczyszczono równoważną impedancję thévenina.

- Rozwiązanie obwodu

Równoważne obliczenia napięcia Thévenina

Po pierwsze, wszelkie obciążenie lub impedancja terminali A i B jest odłączana.

Ponieważ obwód jest znany, siatki lub prawa Kirchhoffa są stosowane w celu znalezienia napięcia na terminalach. To napięcie będzie odpowiednikiem Thévenina.

Może ci służyć: Mount Olympus (Mars)

Równoważne obliczenie impedancji Thévenina

Aby uzyskać równoważną impedancję, przechodzimy do:

- Wymień oryginalne źródła napięcia obwodu na krótkie obwody „Zero impedancji” i źródła oryginalnego obwodu dla otwartej „nieskończonej impedancji”.

- Następnie równoważna impedancja jest obliczana zgodnie z regułami impedancji szeregowej i impedancji równolegle.

Aplikacje Twierdzenia Thévenin (część I)

Zastosujemy twierdzenie Thévenina, aby rozwiązać niektóre obwody. W tej pierwszej części rozważamy obwód, który ma tylko źródła napięcia i rezystancje.

Przykład 1 (obliczenie równoważnego napięcia krok po kroku)

Ryc. 2 pokazuje obwód, który znajduje się w niebieskim pudełku, który ma odpowiednio dwie akumulatory siły elektromotorycznej V1 i V2 oraz rezystancje R1 i R2, obwód ma zaciski A i B, do których można podłączyć obciążenie.

Rysunek 2. Przykład 1 twierdzenia o thévenin. Źródło: Self Made

Celem jest znalezienie równoważnego obwodu théveniny, to znaczy określenie wartości VT i RT obwodu równoważnego.  Zastosuj następujące wartości: V1 = 4 V, V2 = 1 V, R1 = 3Ω, R2 = 6Ω i R = 1Ω.

Krok po kroku

Krok 1 

Określimy napięcie na zaciskach A i B, gdy nie zostaną umieszczone żadne obciążenie.

Krok 2

Obwód do rozwiązania składa się z pojedynczej siatki, za pomocą której prąd rozpowszechniam, że pozytywnie wzięliśmy w kierunku zgodnie z ruchem wskazówek zegara.

Krok 3

Podróżujemy siatką, zaczynając od lewego dolnego rogu. Trasa prowadzi do następującego równania:

V1 - i*r1 - i*r2 - v2 = 0

Krok 4

Wyczyścimy prąd siatki I i uzyskujemy:

I = (v1 -v2) / (r1 +r2) = (4v - 1v) / (3Ω +6Ω) = ⅓ a

Krok 5

Z prądem siatki możemy określić różnicę napięcia lub napięcia między A i B, czyli:

VAB = v1 - i * r1 = 4v - ⅓ a * 3Ω = 3v

To znaczy, że równoważne napięcie Thevenina wynosi: vt = 3v.

Krok 6 (odporność równoważna Thévenin)

Teraz obliczamy równoważny opór Thévenina, dla którego i jak wcześniej powiedziano, źródła napięcia są zastępowane kablem.

W takim przypadku mamy tylko dwie opory równolegle, więc równoważny opór Thévenina to:

RT = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω

Przykład 1b (prąd prąd przy użyciu równoważnika Thévenin)

Podłącz jako obciążenie do zacisków A i B A Rezystancja R = 1Ω do równoważnego obwodu i znajdź prąd, który krąży przez wspomniane obciążenie. 

Może ci służyć: ruch prostoliniowy: cechy, typy i przykłady

Rozwiązanie

Gdy rezystancja R jest podłączona do równoważnego obwodu Thevenin, istnieje prosty obwód, który składa się ze źródła VT, szeregowo oporność z oporem r. 

Nazwimy prąd, który krąży przez obciążenie r, tak aby równanie siatki było takie:

VT - IC* RT - IC* R = 0

Z którego wynika z tego, że IC jest podawany przez:

IC = vt / (rt + r) = 3v / (2Ω + 1ω) = 1 a

Weryfikacja twierdzenia Thévenin

Aby sprawdzić, czy twierdzenie Thévenina jest spełnione, podłącz R do oryginalnego obwodu i znajdź prąd, który krąży przez R, stosując prawo siatki do powstałego obwodu.

Powstały obwód pozostaje, a jego równania siatki są pokazane na poniższym rysunku:

Rysunek 3. Prądy siatkowe. (Własne opracowanie)

Dodając równania siatki, można znaleźć prąd o siatkę I1 w zależności od prądu I2. Następnie zostaje zastąpiony w równaniu drugiej siatki i istnieje równanie z i2 jako jedynym nieznanym. Poniższa tabela pokazuje operacje.

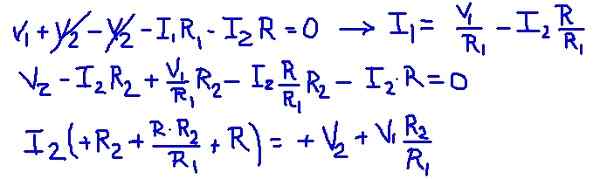Rysunek 4. Szczegół operacji. (Własne opracowanie)

Następnie wymieniane są wartości rezystancji i napięcia źródeł, uzyskując wartość numeryczną prądu siatki I2.

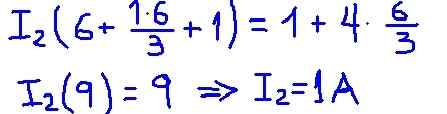Rysunek 5. Szczegół. (Własne opracowanie)

Strumień siatki I2 to prąd, który krąży przez rezystancję obciążenia R, a wartość znaleziona z 1 A w pełni pokrywa się z tym, co wcześniej znaleziono z równoważnym obwodem théveniny.

Zastosowanie twierdzenia Thévenina (część II)

W tej drugiej części twierdzenie Thévenina zostanie zastosowane w obwodzie, który ma źródła napięcia, źródło prądu i rezystancje. 

Przykład 2a (odporność równoważna Thévenin)

Celem jest określenie równoważnego obwodu théveniny odpowiadającego obwodzie poniższego rysunku, gdy zaciski są bez rezystancji 1 omo, wówczas rezystancja jest umieszczona, a prąd prąd jest określany przez tę samą.

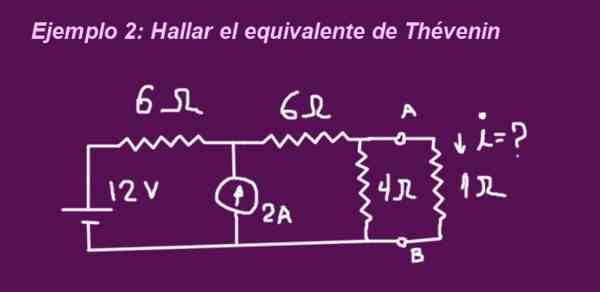Rysunek 6. Przykład 2 obwód. (Własne opracowanie)

Rozwiązanie

Aby znaleźć równoważną rezystancję, rezystancja obciążenia jest usuwana (w tym przypadku 1 Ohmio). Ponadto źródła napięcia są zastępowane przez zwarcie i źródła prądu otwartym obwodem. 

W ten sposób obwód, do którego obliczona zostanie równoważna rezystancja, jest ten pokazany poniżej:

Może ci służyć: Boltzmann stała: historia, równania, obliczenia, ćwiczenia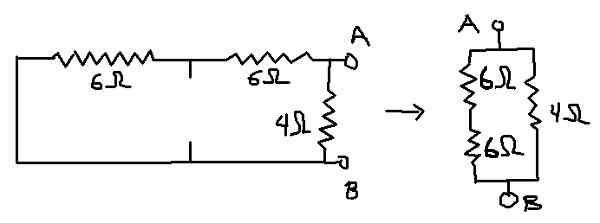Rysunek 7. Szczegół dla obliczenia równoważnego oporu (własne opracowanie)

Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω, który jest równoważną rezystancją Thevenin (RTH).

Przykład 2b 

Obliczyć równoważne napięcie Thévenina.

Rozwiązanie

Aby obliczyć równoważne napięcie théveniny, rozważamy następujący obwód, w którym umieścimy prądy w I1 i I2 w gałęziach wskazanych na poniższym rysunku:

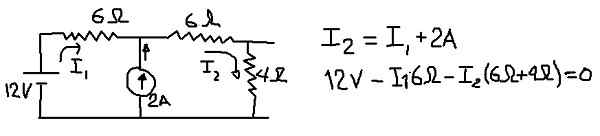Cyfra 8. Szczegóły dotyczące obliczania napięcia Thévenina. (Własne opracowanie)

Na poprzedniej rysunku równanie bieżących węzłów i równanie napięć są pokazane podczas przemieszczenia siatki zewnętrznej. Z drugiego równania obecne I1 jest wyczyszczone:

I1 = 2 - i2*(5/3)

To równanie jest zastąpione w równaniu węzłów:

I2 = 2 - (5/3) i2 + 2 ===> i2 (8/3) = 4 ===> i2 = 12/8 = 1,5 a

Oznacza to, że spadek napięcia w rezystancji 4 omów wynosi 6 woltów.

Krótko mówiąc, napięcie thévenina wynosi vth = 6 v.

Przykład 2C

Znajdź równoważny obwód Thevenin i Prąd w rezystancji obciążenia.

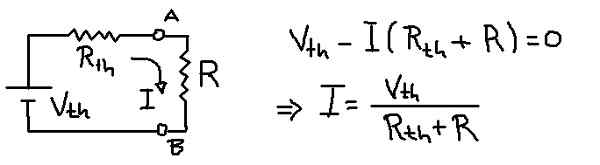Rysunek 9. Prąd w obciążeniu z równoważnikiem Thévenin. (Własne opracowanie)

Rozwiązanie

Poprzednia rysunek pokazuje równoważny obwód théveniny z odpornością na obciążenie r. Z równania napięcia w siatce prąd I, który krąży przez rezystancję obciążenia R jest wydedukowane.

I = vth / (rth + r) = 6 V / (3Ω + 1ω) = 1,5 a

Zastosowanie twierdzenia Thévenina (część III)

W tej trzecie. 

Przykład 3

Celem jest znalezienie równoważnego obwodu Thévenin następującego obwodu:

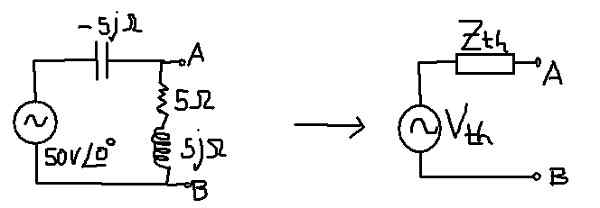Rysunek 10. Thévenin w naprzemiennym obwodzie prądowym. (Własne opracowanie)

Rozwiązanie

Równoważna impedancja odpowiada impulsowi kondensatora równolegle z kombinacją serii oporności i indukcyjności.

Odwrotność równoważnej impedancji jest podana przez:

ZEQ^-1 = (-5J)^-1 + (5 + 5J)^-1 = (1/5) J + ((1/10 + (1/10) J) = (1/10 + 3/ 10 J) MHO

A równoważna impedancja będzie wtedy:

ZEQ = (1 - 3 J) Ohm

Złożony prąd, który można wywnioskować z równania siatki:

50 VV0 - I (-5 J + 5 + 5J) = 50 VV0 - i*5 = 0 ===> i = 10a ∠0 

Teraz obliczany jest spadek napięcia w oporności plus indukcyjność, to znaczy napięcie VAB, które będzie równoważne napięcie thévenin:

VAB = i * (5 + 5 J) ω = 10a ∠0 * 5ω dodaj 45º = 50 V 45º

Innymi słowy

Bibliografia

1. Samouczki elektroniczne, twierdzenie Thevenina. Odzyskane z: elektroniki-tormales.WS
2. Teoria sieci Pytania i odpowiedzi. Twierdzenie Thevenina. Odzyskane z: Sanfoundry.com
3. Twierdzenie Thevenina. Procedura krok po kroku. Odzyskane z: Electrictechnology.org
4. Twierdzenie Thevenina. Rozwiązany przykład krok po kroku. Źródło: Electicalsimple.Blogspot.com
5. Warsztaty na temat twierdzeń Thevenina i Nortona. Źródło: Web.iit.Edu
6. Wikipedia. Twierdzenie Thévenin. Odzyskane z: Wikipedia.com