Twierdzenie Chebyshova, że ​​aplikacje i przykłady

On Twierdzenie Chebyshova (lub nierówność Chebyshova) jest jednym z najważniejszych klasycznych wyników teorii prawdopodobieństwa. Umożliwia oszacowanie prawdopodobieństwa zdarzenia opisanego w kategoriach zmiennej losowej x, zapewniając nam poziom, który nie zależy od rozkładu zmiennej losowej, ale od wariancji x.

Twierdzenie nazywane jest na cześć rosyjskiej matematyki.

Ta nierówność lub te, które ze względu na ich cechy nazywane są nierównością Chabyshova, jest wykorzystywana głównie do przybliżania prawdopodobieństwa za pomocą poziomów obliczania.

Jakie jest twierdzenie Chebyshova?

W badaniu teorii prawdopodobieństwa zdarza się, że jeśli funkcja rozkładu zmiennej losowej x jest znana, jego oczekiwana wartość można obliczyć - lub matematyczną nadzieję i (x) - i jej wariancję var (x), o ile one długo te Istnieją kwoty. Jednak wzajemność niekoniecznie jest prawdziwa.

Oznacza to, że znajomość e (x) i var (x) niekoniecznie może uzyskać funkcję rozkładu x, więc wielkości takie jak p (| x |> k) dla niektórych k> 0 są bardzo trudne do uzyskania. Ale dzięki nierówności Chebyshova możliwe jest oszacowanie prawdopodobieństwa losowej zmiennej.

Twierdzenie Chebyshova mówi nam, że jeśli mamy zmienną losową X na próbce z funkcją prawdopodobieństwa p, a jeśli k> 0, to:

Może ci służyć: trójkąt acutangle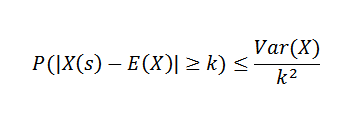

Aplikacje i przykłady

Wśród wielu aplikacji, które posiada twierdzenie Chebyshova, można wymienić następujące:

1. Limit prawdopodobieństwa

Jest to najczęstsza aplikacja i służy do podania górnego poziomu dla p (| x-e (x) | ≥K), gdzie k> 0, tylko z wariancją i nadzieją zmiennej losowej x, bez znajomości funkcji prawdopodobieństwa, nie znając funkcji prawdopodobieństwa.

Przykład 1

Załóżmy, że liczba produktów wytwarzanych w firmie przez tydzień jest losową zmienną ze średnią 50.

Jeśli wiadomo, że wariancja tygodnia produkcji wynosi 25, to, co możemy powiedzieć o prawdopodobieństwie, że w tym tygodniu produkcja różni się o ponad 10?

Rozwiązanie

Stosując nierówność Chebyshova, którą musimy:

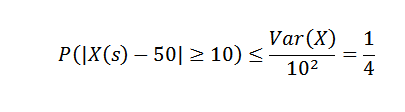
Z tego możemy uzyskać, że prawdopodobieństwo, że w tygodniu produkcyjnym liczba elementów przekracza ponad 10 do średniej, wynosi najwięcej 1/4.

2. Demonstracja twierdzeń o limicie

Nierówność Chebyshova odgrywa ważną rolę w wykazaniu najważniejszych twierdzeń. Jako przykład mamy następujące czynności:

Słabe prawo dużych liczb

To prawo określa, że ​​biorąc pod uwagę sukcesję x1, x2, ..., xn, ... niezależnych zmiennych losowych o tej samej średnim rozkładowi e (xi) = μ i wariancji var (x) = σ², i znana średnia próbka:

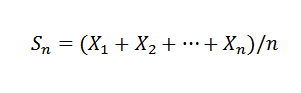
Więc dla k> 0 musisz:

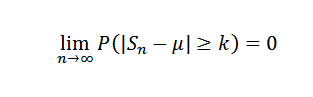
Lub odpowiednik:

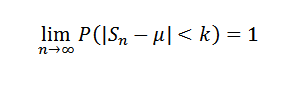
Demonstracja

Najpierw zauważamy następujące:

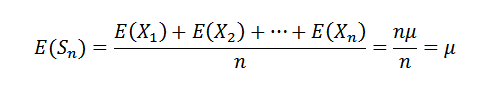
Jak x1, x2, ..., xn są niezależne, wynika z tego, że:

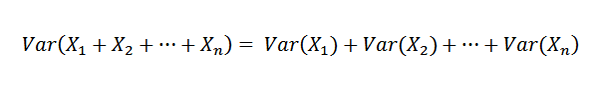
Dlatego możliwe jest potwierdzenie następujących:

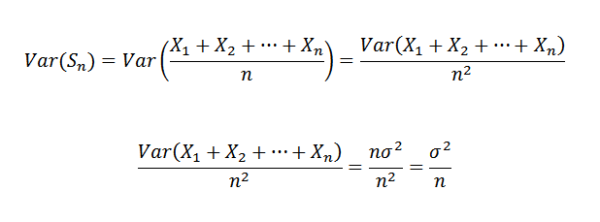
Następnie, używając twierdzenia Chebyshova, musisz:

Może ci służyć: funkcje trygonometryczne: podstawowy, w płaszczyźnie kartezjańskim, przykłady, ćwiczenia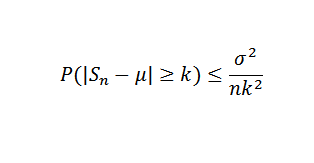

Wreszcie twierdzenie wynika z faktu, że właściwy limit wynosi zero, gdy n ma tendencję do nieskończoności.

Należy zauważyć, że ten test został przeprowadzony tylko w przypadku, w którym istnieje wariancja XI; to znaczy, że się nie rozbiega. Zatem obserwujemy, że twierdzenie jest zawsze prawdziwe, jeśli istnieje e (xi).

Twierdzenie Chebyshova

Jeśli x1, x2, ..., xn, ... jest to sukcesja niezależnych zmiennych losowych, tak że istnieje pewne C0:

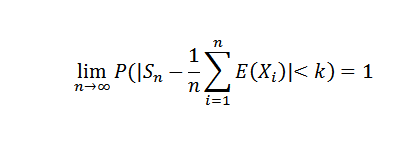
Demonstracja

Ponieważ sukcesja wariancji jest jednolicie ograniczona, mamy to var (Sn) ≤ c/n, dla wszystkich naturalnych n. Ale wiemy o tym:

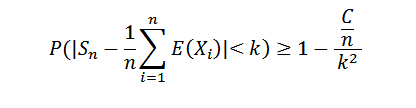
Wykonując N do nieskończoności, jest następujący:

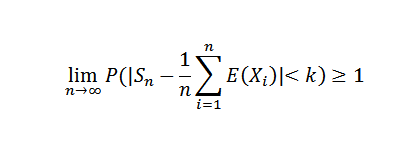
Ponieważ prawdopodobieństwo nie może przekroczyć wartości 1, uzyskuje się pożądany wynik. W wyniku tego twierdzenia moglibyśmy wspomnieć o szczególnym przypadku Bernoulli.

Jeśli eksperyment jest powtarzany niezależnie z dwoma możliwymi wynikami (awaria i sukces), gdzie P jest prawdopodobieństwem sukcesu w każdym eksperymencie, a x jest losową zmienną reprezentującą liczbę uzyskanych sukcesów, to dla każdego K> 0 musisz:

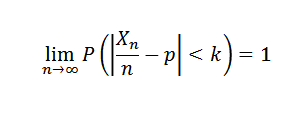
3. Wielkość próbki

Jeśli chodzi o wariancję, nierówność Chabyshova pozwala nam znaleźć wielkość próbki, która jest wystarczająca, aby zapewnić prawdopodobieństwo, że | sn-μ |> = k, jest tak małe, jak to wymaga, co pozwala na podejście do podejścia do przeciętny.

Dokładnie, czy to x1, x2, ... xn próbka niezależnych zmiennych losowych o wielkości n i przypuść, że e (xi) = μ i jego wariancja σ². Tak więc, ze względu na nierówność Chebyshova, musisz:

Może ci służyć: numer lub liczba eulera E: Ile OK, właściwości, aplikacje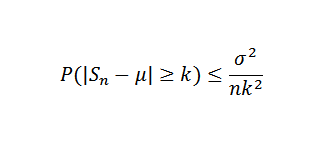

Teraz bądź δ> 0 stał. Musimy:

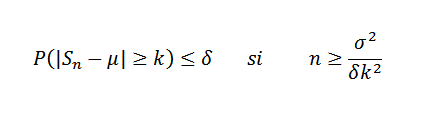
Przykład

Załóżmy, że x1, x2, ... xn to próbka niezależnych zmiennych losowych z rozkładem Bernoulli, tak że przyjmują wartość 1 z prawdopodobieństwem p = 0.5.

Jaka powinna być wielkość próby, aby zapewnić prawdopodobieństwo, że różnica między arytmetyczną średnią SN a jego oczekiwaną wartością (która przekracza więcej niż 0,1), jest mniejsza lub równa 0.,01?

Rozwiązanie

Musimy (x) = μ = p = 0,5 i co var (x) = σ²= P (1-p) = 0,25. Dla nierówności Chebyshova dla każdego k> 0 musimy:

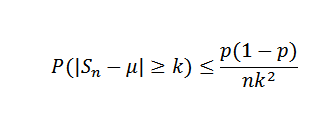
Teraz biorąc k = 0,1 i δ = 0,01, musisz:

W ten sposób stwierdzono, że potrzebna jest wielkość próbki wynosząca co najmniej 2500, aby zapewnić prawdopodobieństwo zdarzenia | Sn - 0,5 |> = 0,1 jest mniejsze niż 0,01.

Nierówności typu Chebyshova

Istnieją różne nierówności związane z nierównościami Chebyshova. Jednym z najbardziej znanych jest nierówność Markowa:

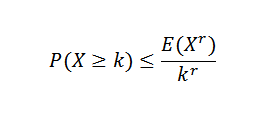
W tym wyrażeniu x jest to niezmienna zmienna losowa z k, r> 0.

Nierówność Markowa może przybierać różne formy. Na przykład albo i niechazyjna zmienna losowa (więc p (y> = 0) = 1) i przypuść, że istnieje E (y) = μ. Załóżmy również, że (e (y))^R= μ_R Jest dla pewnej liczby całkowitej r> 1. Więc:

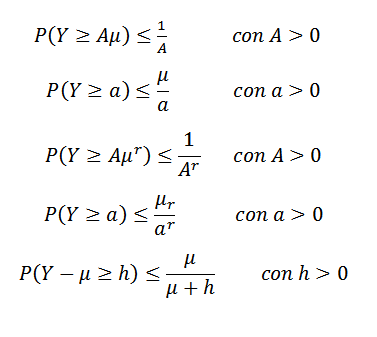
Kolejną nierównością jest Gauss, który mówi nam, że biorąc pod uwagę unimodalną X zmienną losową z modą przy zero, a następnie dla K> 0,