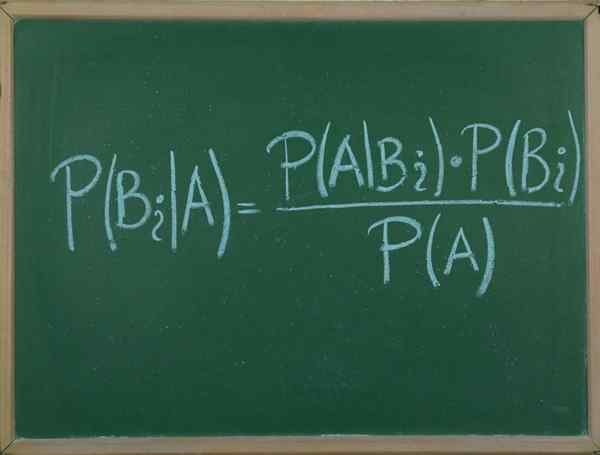Twierdzenie Bayesa
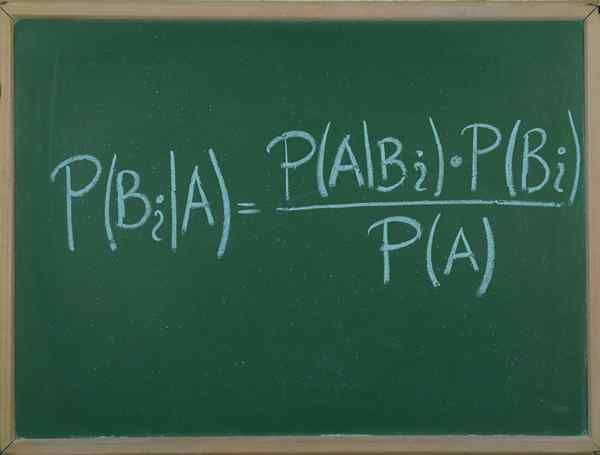
- 4131
- 568
- Herbert Wróblewski
Wyjaśniamy, jakie jest twierdzenie Bayesa, jego zastosowania i rozwiązywane ćwiczenia
Jakie jest twierdzenie Bayesa?
On Twierdzenie Bayesa Jest to procedura, która pozwala nam wyrazić warunkowe prawdopodobieństwo losowego zdarzenia A kości B, pod względem rozkładu prawdopodobieństwa podanego zdarzenia B i rozkładu prawdopodobieństwa tylko do TO.
Twierdzenie to jest bardzo przydatne, ponieważ dzięki nim możemy powiązać prawdopodobieństwo, że zdarzenie A zdarza się, wiedząc, że B się dzieje, z prawdopodobieństwem, że nastąpi przeciwnie, to znaczy, że występuje podane.
Twierdzenie Bayesa było srebrną propozycją wielebnego Thomasa Bayesa, osiemnastego angielskiego teologa, który był także matematykiem. Był autorem kilku miejsc pracy w teologii, ale obecnie jest znany z kilku traktatów matematycznych, w tym twierdzenie Bayesa już wspomniane jako główny wynik.
Bayes poradził sobie z tym twierdzeniem w pracy zatytułowanej „Esej na temat rozwiązania problemu w doktrynie szans” (esej na temat rozwiązania problemu w doktrynie możliwości), opublikowanym w 1763 r. I na którym duże opracowały badania z aplikacjami w różnych dziedzinach wiedzy.
Wyjaśnienie
Po pierwsze, w przypadku większej kompresji tego twierdzenia konieczne są pewne podstawowe pojęcia teorii prawdopodobieństwa, zwłaszcza twierdzenie mnożenia dla warunkowego prawdopodobieństwa, które to określa
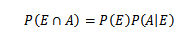
Dla e i arbitralne zdarzenia z przykładowej przestrzeni s.
Oraz definicja partycji, która mówi nam, że mamy1 ,DO2,… , DON zdarzenia z przykładowej przestrzeni, utworzą partycję s, jeśli aSiema Są wzajemnie wykluczające się, a ich związek jest s.
Może ci służyć: po co są liczby? 8 głównych zastosowańMając to, czy to kolejne wydarzenie. Więc możemy zobaczyć B jako
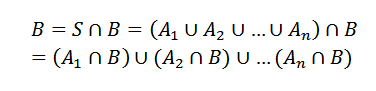
GdzieSiema Przecinane z B są wzajemnie wykluczające się zdarzenia.
I w konsekwencji,
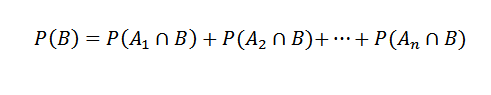
Następnie zastosowanie twierdzenia mnożenia
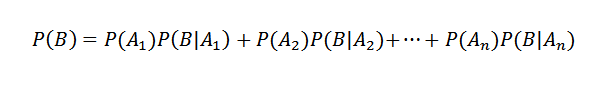
Z drugiej strony, warunkowe prawdopodobieństwo AI B jest zdefiniowane przez
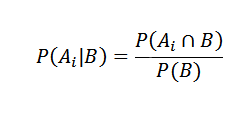
Zastępując prawidłowo, mamy to dla każdego i
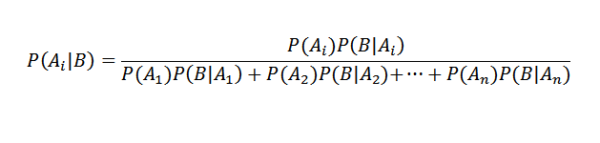
Zastosowania Bayes Twierdzenie
Dzięki temu wynikowi grupy badawcze i różnorodne korporacje udało się ulepszyć systemy oparte na wiedzy.
Badanie choroby
Na przykład w badaniu chorób twierdzenie Bayesa może pomóc w rozpoznaniu prawdopodobieństwa, że choroba zostanie znaleziona u grupy osób z daną cechą, przyjmując jako dane globalne wskaźniki choroby i przewagę wspomnianych cech w obu Zdrowie i chorzy ludzie.
Rozwój oprogramowania
Z drugiej strony, w świecie wysokich technologii, wpłynęło to na duże firmy, które rozwinęły się, dzięki temu wyniku, oprogramowania „opartym na wiedzy”.
Jako codzienny przykład mamy asystenta Microsoft Office. Twierdzenie Bayesa pomaga oprogramować ocenić problemy, które użytkownik przedstawia, i ustalić, jakie porady udzielają, a tym samym być w stanie zaoferować lepszą usługę zgodnie z nawykami użytkownika.
Należy zauważyć, że ta formuła była ignorowana do niedawna, dzieje się tak głównie dlatego, że kiedy ten wynik został opracowany 200 lat temu, niewiele było dla nich praktycznego zastosowania. Jednak w naszych czasach, dzięki wielkim postępom technologicznym, naukowcy osiągnęli sposoby na zastosowanie tego wyniku w praktyce.
Rozwiązane ćwiczenia
Ćwiczenie 1
Firma telefoniczna ma dwie maszyny A i B. 54% telefonów komórkowych jest wytwarzanych przez maszynę A, a resztę według maszyny B. Nie wszystkie telefony komórkowe są w dobrym stanie.
Może ci służyć: czynnikowanieOdsetek wadliwych telefonów komórkowych wykonanych przez A wynosi 0.2, a dla B to 0.5. Jakie jest prawdopodobieństwo, że telefon komórkowy wspomnianej fabryki jest wadliwy? Jakie jest prawdopodobieństwo, że wiedza, że telefon komórkowy jest wadliwy, pochodzi z maszyny?
Rozwiązanie
Tutaj masz eksperyment przeprowadzony w dwóch częściach; W pierwszej części zdarzenia występują:
Do: telefon komórkowy wykonany przez maszynę A.
B: Telefon komórkowy wykonany przez maszynę B.
Ponieważ maszyna A wytwarza 54% telefonów komórkowych, a reszta jest wytwarzana przez maszynę B, maszyna B musi wytwarzać 46% telefonów komórkowych. Szanse na te wydarzenia są dane, a mianowicie:
P (a) = 0,54.
P (b) = 0,46.
Wydarzenia drugiej części eksperymentu to:
D: Wadliwy telefon komórkowy.
E: Komórka niezadowująca.
Jak stwierdzono w stwierdzeniu, prawdopodobieństwo tych zdarzeń zależą od wyniku uzyskanego w pierwszej części:
P (d | a) = 0,2.
P (D | B) = 0,5.
Korzystając z tych wartości, możesz również określić prawdopodobieństwa akcesoriów tych zdarzeń, to znaczy:
P (e | a) = 1 - p (d | a)
= 1 - 0,2
= 0,8
I
P (E | B) = 1 - P (D | B)
= 1 - 0,5
= 0,5.
Teraz wydarzenie D można zapisać w następujący sposób:
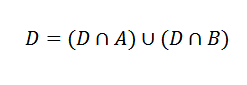 Te wydarzenia wykluczają się wzajemnie.
Te wydarzenia wykluczają się wzajemnie.
Zastosowanie twierdzenia mnożenia dla prawdopodobieństwa warunkowego wynosi:
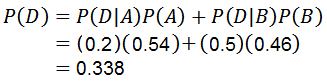
Z którymi udzielono odpowiedzi na pierwsze pytanie.
Teraz musimy tylko obliczyć P (A | D), do którego zastosowano twierdzenie Bayesa:
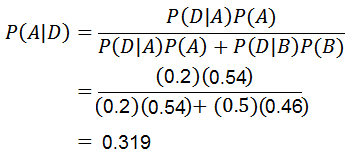
Dzięki twierdzeniu Bayesa można potwierdzić, że prawdopodobieństwo, że telefon komórkowy został wykonany przez maszynę A, wiedząc, że telefon komórkowy jest wadliwy, wynosi 0.319.
Może ci służyć: icosagonoĆwiczenie 2
Trzy pudełka zawierają czarne i czarne kulki. Skład każdego z nich jest następujący: u1 = 3b, 1n, u2 = 2b, 2n, u3 = 1b, 3n.
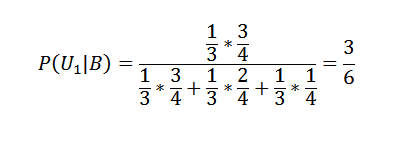
Losowo wybrany jedno z pudełek i losowa kula jest z niej wyodrębniana, która okazuje się biała. Jakie jest pudełko z wybranymi najprawdopodobniej?
Rozwiązanie
Za pośrednictwem U1, U2 i U3 będziemy również reprezentować wybraną skrzynkę.
Wydarzenia te stanowią partycję S i zweryfikuje się, że p (u1) = p (u2) = p (u3) = 1/3, ponieważ wybór pola jest losowy.
Jeśli B = Wyodrębniona kula jest biała, będziemy mieć p (b | u1) = 3/4, p (b | u2) = 2/4, p (b | u3) = 1/4 .
Chcemy uzyskać prawdopodobieństwo, że piłka została pobrana z pudełka IU, wiedząc, że ta piłka jest biała, to znaczy p (ui | b) i widząc, która z trzech wartości była najwyższa do wiedzy, która z których pudełko jest bardziej skłonne do ekstrakcji białej kulki.
Stosowanie twierdzenia Bayesa do pierwszego z pudeł:
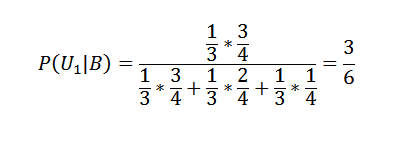
I dla pozostałych dwóch:
P (u2 | b) = 2/6 i p (u3 | b) = 1/6.
Następnie pierwszy z pudełek jest tym, który ma większe prawdopodobieństwo, że został wybrany do ekstrakcji białej kulki.