Rozpadły się aplikacje Fouriera, przykłady i ćwiczenia

Seria Fouriera Składają się one z sumy nieskończonych terminów, które składają się z funkcji harmonicznych, zatok i cosinus, których argument jest całą podstawową częstotliwością.

Funkcje sinusoidalne i cosinusowe są mnożone przez współczynniki wartości, tak że suma jest identyczna z funkcją z okresem T równym dwukrotnie PI (2π) podzielonym przez podstawową częstotliwość kątową ω ω.

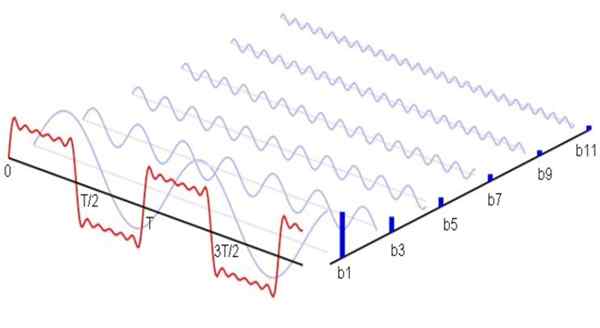
Rysunek 1. Oto (w kolorze niebieskim) pierwsze harmoniczne non -null z serii Fouriera odpowiadające sygnałowi przebiegu kwadratowego. Suma harmoniczna powoduje powstanie czerwonego sygnału. Źródło: Wikimedia Commons.

Matematycznie, że zostanie to wyrażone w następujący sposób: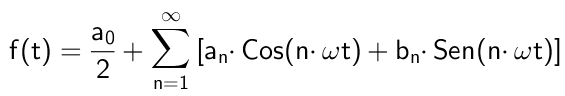

Gdzie Ω Jest to podstawowa częstotliwość związana z okresem T funkcji f (t) Poprzez związek: 

Ω = 2π / t

Na okres okresowy T, funkcja f (t) spełnia ten warunek:

f (t) = f (t + k t)

Gdzie k Jest to liczba całkowita i współczynników₀ , Do_N oraz b_N Nazywane są Współczynniki Fouriera.

[TOC]

Znaczenie i wykorzystanie serii Fouriera

Nazwa serii Fouriera wynika z faktu, że jego odkrywcą był francuski matematyka.

Odkrycie to było fundamentalne dla matematyki, ponieważ jeśli równanie różniczkowe ma określone rozwiązanie harmoniczne, wówczas możliwe jest osiągnięcie ogólnego rozwiązania za pomocą nakładania się lub suma tego samego.

Współczynniki Fouriera funkcji okresowej, zwane również podpisać, Są to spektrum tego samego.

Dlatego widmo jest zbiorem częstotliwości, które tworzą sygnał charakteryzujący się amplitudą każdej częstotliwości, co odpowiada wartościom współczynników Fouriera.

Systemy kompresji sygnału lub przebiegi audio i wideo, z tyłu znacznie mniejszą liczbę bitów niż oryginalny cyfrowy sygnał.

Seria sygnału Fouriera jest jak jego odcisk palca, w tym sensie, że znane współczynniki, które go składają, zawsze możesz wiedzieć, który znak należą.

Chociaż użycie serii Fouriera lub jej najbardziej ogólnej formy, Transformacja Fouriera, Jako metodę kompresji sygnału znana jest od dłuższego czasu, jego zastosowanie w praktyce musiało wystarczająco szybko czekać na procesory numeryczne, co pozwoliło na ściskanie sygnałów i dekompresję w „w czasie rzeczywistym”.

Może ci służyć: zmienne statystyczne

Przykład serii Fouriera 

Następnie przykład funkcji F (t) i jej serii Fouriera.

Funkcja to:

 f (t) = 0 tak 0 ≤ t  < π y 1 si π ≤  t   < 2π

I ma odpowiednią serię Fouriera podaną przez:

f (t) = ½ - 2/π⋅se (t) - 2/(3π) ⋅se (3T) - 2/(5π) ⋅sen (5t) - 2/(7π) ⋅sen (7t) -…

Poniższy rysunek pokazuje funkcję i częściową sumę serii Fouriera:

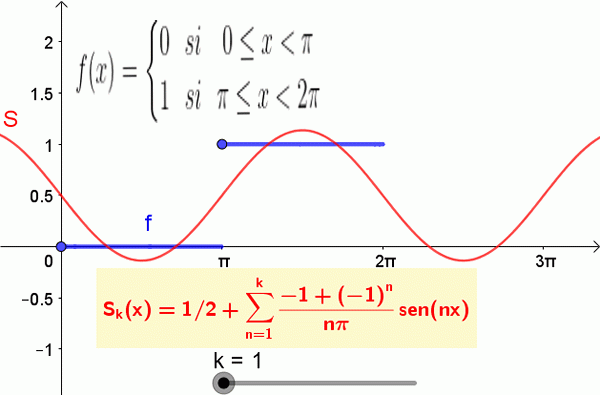Rysunek 2. Pokazano pierwsze 19 terminów sumę Fouriera odpowiadających funkcji kroku. Źródło: f. Zapata.

Określenie współczynników

Poniżej znajduje się sposób określenia współczynników Fouriera:

Załóżmy, że funkcja jest zdefiniowana f (x) w przedziale wynikającym z t_Siema do t_Siema + T, gdzie kapitał będzie okresem funkcji. Wtedy jego seria Fouriera to:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 ω t) +… + a_N Cos (n ω t) +…

.. .+ B₁ sin (ω t) +b₂ sin (2 ω t) +… +b_N Sin (n ω t) +..

Obliczanie niezależnego terminu

Aby znaleźć niezależny termin, integrujemy obu członków równości w przedziale definicji funkcji:

[T_Siema , T_Siema+ T]

Dlatego:

To samo_N ∫cos (n ω t) dt +…

.. .+ B₁ ∫Sen (ω t) dt +b₂ ∫Sen (2 ω t) dt +… +b_N ∫Sen (n ω t) dt +…

Tutaj symbol ∫ oznacza całkę zdefiniowaną z t_Siema do t_Siema + T.

Integralą pierwszego terminu jest t, która oceniona w górnej granicy wynika:

T_Siema + T

Po odjęciu dolnej granicy t_Siema, w ostatecznym t.

Wszystkie inne terminy to 0, ponieważ są to funkcje cosinusowe lub zatokowe oceniane w pełnym okresie, jak pokazujemy poniżej:

∫COS (nω t) dt = (1/ nω) ∫cos (nω t) d (nω t)

Pamiętaj, że symbol ∫ oznacza integrację między t_Siema do t_Siema + T. 

Aby integracja terminów, które mają cosinus lub pierś, dokonamy następującej zmiany zmiennej:

x = ω (t - t_Siema)

Tak więc różnica X, Dx jest równa różnicy D (ωt).

Zatem integralną częścią, którą należy przeprowadzić, to:

Ponieważ n jest liczbą całkowitą, wówczas zdefiniowana całka zawsze daje zero. To samo dotyczy funkcji sinusoidalnej.

Dlatego zdefiniowana całka oceniona w pełnym okresie wszystkich warunków zawiera. 

Może ci służyć: podziały, w których pozostałość wynosi 300

Stwierdzono zatem, że termin a₀ jest obliczany w następujący sposób:

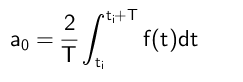
Obliczanie współczynników

Aby obliczyć współczynniki, które mnożą się do funkcji cosinus, obaj członkowie równości muszą zostać pomnożeni:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 ω t) +… + a_N Cos (n ω t) +…

.. .+ B₁ sin (ω t) +b₂ sin (2 ω t) +… +b_N Sin (n ω t) +..

Przez funkcję cosinusową ocenioną w odpowiedniej harmonicznej, a następnie integral zdefiniowany w pełnym okresie dla obu członków. 

Na przykład, aby obliczyć_M Obaj członkowie są mnożone przez COS (MωT):

f (t) cos (m ω t) = a₀/2 cos (m ω t) + a₁ cos (ω t) cos (m ω t) + a₂ cos (2 ω t) cos (m ω t) +… + Do_N Cos (n ω t) cos (m ω t) +…

.. .+ B₁ sin (ω t) cos (m ω t) +b₂ sin (2 ω t) cos (m ω t) +… +b_N Sin (n ω t) cos (m ω t) +..

Następnie zintegruj się z pełnym okresem, to znaczy w przedziale wynikającym z T_Siema do t_Siema + T.

Integra terminu zawierającego A₀ jest anulowana, ponieważ M jest liczbą całkowitą, a funkcja cosinusowa jest zintegrowana z pełnym okresem. 

Integrale zawierające produkt cos (n ω t) cos (m ω t) są również unieważnione za każdym razem, gdy n ≠ m. Tylko w przypadku, że n = m ma całkę:

Wszystkie terminy, które mają mnożoną sinus cosinus, to znaczy te, które są mnożone przez współczynniki B, jako zawierające całki typu Sen (n ω t) cos (m ω t), gdy określona całka jest wykonywana na kompletnym okres. 

Stąd stąd stwierdzono, że:

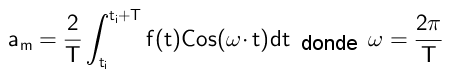
Obliczanie współczynników B

Aby znaleźć współczynniki B, zastosowano podobną procedurę, ale tym razem obaj członkowie funkcji dopasowane do serii Fouriera są mnożone przez funkcję SEN (M ω t).

Z tych samych powodów już wyjaśniono w przypadku, w którym jedynym terminem, który nie jest unieważniony po zintegrowaniu z pełnym okresem, jest taki, w którym:

n = m

I gdzie pojawia się całka [Sen (M ω t)]]², To zintegrowane w pełnym okresie powoduje π.

Może ci służyć: funkcja homograficzna: jak wykres, rozwiązane ćwiczenia

W ten sposób współczynniki B są obliczane zgodnie z następującym wzorem:

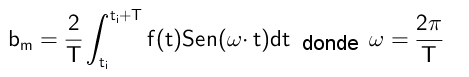
Ćwiczenia

- Ćwiczenie 1

Wykonaj wyraźne obliczenie współczynników funkcji

 f (t) = 0 tak 0 ≤ t  < π y 1 si π ≤  t   < 2π

Rozwiązanie

Najpierw identyfikujemy okres t tej funkcji jako 2π, więc częstotliwość podstawowa ω = 2π/ t w tym przykładzie jest równa jednostce, to znaczy:

Ω = 1

Funkcja jest zdefiniowana w przedziale [0, 2π], więc wszystkie integracje zostaną przeprowadzone we wspomnianym przedziale. 

Następnie niezależny termin jest obliczany w następujący sposób:

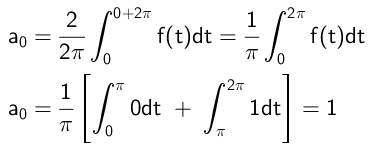
Współczynniki, które mnożą się do funkcji cosinus, są obliczane w ten sposób:

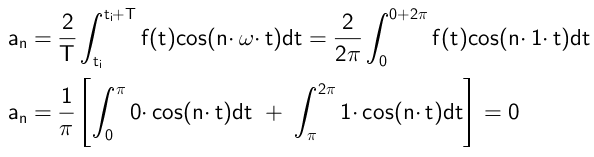
Jak widać, wszystkie współczynniki są zerowe, co się stanie, pod warunkiem, że funkcja f (t) jest dziwna.

Podobnie współczynniki B zostaną obliczone w następujący sposób:

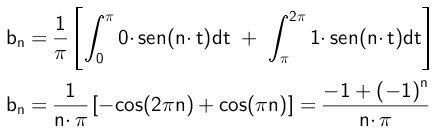
- Ćwiczenie 2

Znajdź współczynniki funkcji odpowiadającej ryc. 1, czyli:

f (t) = -1 tak 0 ≤ t

Rozwiązanie 

Ponieważ funkcja przyjmuje wartości między -1 do +1, możemy intuitować, że niezależny termin jest nieważny, jednak wyraźnie ją obliczamy:

Z powodu faktu, że funkcja ma dziwną symetrię, wszystkie współczynniki, które pomnożą terminy harmoniczne z funkcją cosinus, muszą być nieważne. Weryfikujemy to poniżej:

Na koniec znajdziemy współczynniki B, które mnożą terminy harmoniczne zawierające funkcję zatok:

Gdzie można zauważyć wszystkie warunki B z indeksem dolnym UP, wynoszą 0. Pierwsze dziwne warunki to:

B₁= -4/(π); B₃= -4/(3π); B₅= -4/(5π); B₇= -4/(7π) i b₉= -4/(9π)

https: // youtu.BE/737YAGWSYZYA

Bibliografia

1. Amerror, ja. 2013. Opanowanie dyskretnej transformacji Fouriera w jednym, dwóch lub kilku wymiarach: pułapki i artefakty. Springer Science & Business Media.
2. Briggs, w. 1995. DFT: Podręcznik właścicieli dyskretnej transformacji Fouriera. Syjam.
3. Chu, e. 2008. Dyskretne i ciągłe transformacje Fouriera: analiza, aplikacje i szybkie algorytmy. CRC Press.
4. Guoan Bi, Yonghong Zeng. 2012. Transformacje i szybkie algorytmy do analizy sygnału i reprezentacji. Springer Science & Business Media.
5. Sundararajan, zm. 2003. Cyfrowe przetwarzanie sygnału: teoria i praktyka.Światowe naukowe. 
6. Wikipedia. Seria Fouriera. Odzyskane z: jest.Wikipedia.com