Rozkład częstotliwości Jak zrobić tabelę, przykład, ćwiczenie

A Rozkład częstotliwości W statystykach odnosi się to do trendu, która jest zgodna z danymi zorganizowanymi w grupach, kategoriach lub klasach, gdy każdy z nich przypisuje się liczbę o nazwie częstotliwość, która wskazuje, ile danych jest w każdej grupie. 

Z reguły obserwuje się, że częstotliwości te są rozmieszczone wokół grupy centralnej: ta z największą liczbą danych.

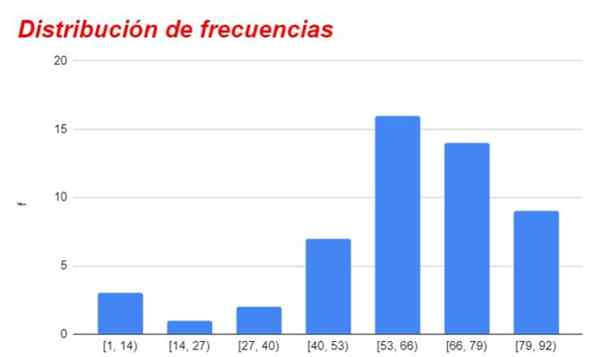
Rysunek 1. Wykres rozkładu częstotliwości uzyskany z odpowiedniej tabeli. Źródło: f. Zapata.

Grupy, które są powyżej lub poniżej, wspomniane centralna kategoria stopniowo zmniejszają ich częstotliwość, będąc bardzo małymi lub nieistotnymi dla kategorii najdalej od kategorii o wyższej częstotliwości.

Sposób poznania rozkładu częstotliwości zestawu danych polega na tworzeniu kategorii, a następnie tworzeniu tabeli częstotliwości. Wizualna reprezentacja tabeli częstotliwości nazywa się histogramem.

[TOC]

Typy częstotliwości

Istnieje kilka rodzajów częstotliwości:

1.- Absolutna frecuencja: Jest najbardziej podstawowy, a z niego pozostałe są zbudowane. Po prostu składa się z całkowitej liczby danych odpowiadających kategorii.

2.- Częstotliwość względna: Jest to bezwzględna częstotliwość każdej kategorii podzielonej przez całkowitą liczbę danych.

3.- Częstotliwość procentowa: Jest to ta sama częstotliwość względna, ale pomnożona przez sto, co wskazuje na procent wyglądu wartości w każdej kategorii.

4.- Zgromadzona częstotliwość: Jest to suma bezwzględnych częstotliwości kategorii niższych lub równych rozważanej kategorii. 

5.- Procent skumulowana częstotliwość: Jest to suma procentowych częstotliwości kategorii niższych lub równych obserwowanej kategorii.

Kroki, aby zrobić tabelę rozkładu częstotliwości

Aby zbudować tabelę rozkładu częstotliwości, należy wykonać kilka kroków.

Po pierwsze, dane muszą mieć drzewo itp.

Może ci służyć: jakie są dzielniki 30? (Wyjaśnienie)

Krok 1

Zidentyfikuj minimalną wartość Xmin i maksymalna wartość Xmax W zestawie danych X.

Krok 2

Oblicz zakres R, który jest zdefiniowany jako różnica między wartością maksymalną mniejszą wartością minimalną: r = xmax - xmin.

Krok 3

Określ liczbę k odstępów lub klas, które mogą być wstępnie ustalone. Numer k określi liczbę wierszy, które będzie miała tabela częstotliwości.

Krok 4

W przypadku liczby interwałów k Nie jest to wcześniej podane, wówczas należy go ustalić zgodnie z następującymi wytycznymi: najmniejsza liczba zalecanych kategorii to 5, ale może być wyższa w takim przypadku, że preferowane jest wybrać liczbę nieparzystą.

Krok 5

Istnieje formuła o nazwie Schowers To daje nam liczbę interwałów k Zalecane dla zestawu, który składa się z N dane:

K = [1 + 3322⋅log n]

W rezultacie w wspornikach z pewnością będzie liczbą rzeczywistą, wspornik wskazuje, że musi być zaokrąglony do najbliższej nieparzystej liczby całkowitej, aby uzyskać wartość liczb całkowitą k.

Krok 6

Amplituda jest obliczana DO każdego interwału (klasy lub kategorii) przyjmujący iloraz między zakresem R i liczba interwałów k: A = r/k. Jeśli oryginalne dane są liczbami, wówczas najbliższa liczba całkowita jest zaokrąglona, ​​w przeciwnym razie realna wartość pozostaje.

Krok 7

Określić dolne i górne granice każdego przedziału lub klasy. Pierwszy przedział lub najniższa klasa ma dolną granicę najmniejszą z oryginalnych danych, to znaczy li = xmin i jako górna granica wartość minimalna plus amplituda interwału, jest to ls = xmin + a. 

Krok 8

Kolejne interwały to: 

[[[Xmin, xmin + a), [ Xmin + a, xmin + 2⋅a), ... [ Xmin + (k-1) a, xmin + k⋅A).

Może ci służyć: połączone operacje

Krok 9

Marka klasy XC jest określana dla każdego przedziału, przy użyciu następującej wzoru: Xc = (ls - li) / 2 + li.

Krok 10

Nagłówek tabeli częstotliwości jest umieszczany, który składa się z wiersza z następującymi etykietami: klasy, marka klasy XC, częstotliwość F, częstotliwość względna (lub procentowa częstotliwość F%) i skumulowana częstotliwość F (lub skumulowana częstotliwość procentowa F%).

Następnie będziemy następujące:

Pierwsza kolumna tabeli częstotliwości: zawiera interwały lub klasy, w których dane zostały podzielone.

Druga kolumna: zawiera markę klasową (lub punkt pośredni) każdego podinterwale.

Trzecia kolumna: Zawiera bezwzględną częstotliwość F każdej klasy lub kategorii.

Czwarta i piąta kolumna: Wartości odpowiadające częstotliwości względnej (lub procentowej) i skumulowanej częstotliwości F (lub skumulowanej procentowej) są.

Przykład budowy tabeli

Poniższe dane odpowiadają dokładnym odpowiedzi 100 pytań zastosowanych do grupy 52 studentów:

65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55, 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48, 64, 15, 50.

Wykonamy kroki, aby zbudować tabelę częstotliwości:

1.- Minimalne i maksymalne wartości xmin = 1, xmax = 89.

2.- Zakres wynosi: r = 89 - 1 = 88

3.- Określenie liczby przedziałów zgodnie z Schowers: K = [1 + 3322⋅log 52] = [6,70] = 7.

4.- Obliczenie szerokości przedziałów: a = r / k = 88/7 = 12,57 ≈ 13.

5.- Odstępy to: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92).

6.- Marki klasowe każdego przedziału są określone: ​​8, 21, 34, 47, 60, 73 i 86.

7.- Tabela jest wykonana:

Może ci służyć: wewnętrzne i zewnętrzne kąty koniugatu: przykłady, ćwiczenia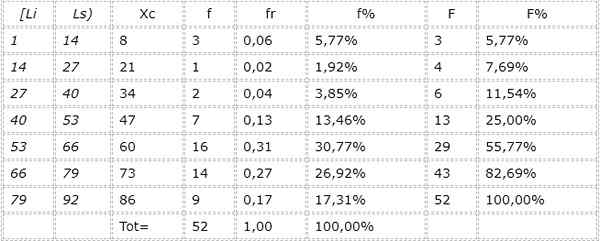

Wykres częstotliwości dla różnych przedziałów lub kategorii pokazano na rycinie 1.

Ćwiczenie rozwiązane

Nauczyciel rejestruje odsetek celów osiągniętych w temacie fizyki dla każdego ucznia. Jednak kwalifikacja dla każdego studenta, chociaż zależy to od odsetka osiągniętych celów, jest ściśle do niektórych kategorii wcześniej ustalonych w regulamentach studiów uniwersyteckich.

Spójrzmy na konkretny przypadek: w sekcji fizyki masz odsetek celów osiągniętych dla każdego z 52 studentów: 

15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61. 65, 70, 89, 64, 54, 85, 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.

W tym przykładzie kategorie lub klasy odpowiadają ostatecznej kwalifikacji przypisanej zgodnie z odsetkiem x osiągniętych celów:

1.- Bardzo biedne: 1 ≤ x < 30

2.- Biedne: 30 ≤ x < 50

3.- Wystarczy: 50 ≤ x < 70

4.- Cóż: 70 ≤ x < 85

5.- Doskonałe: 85 ≤ x ≤ 100

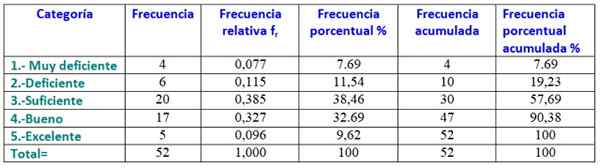
Aby wykonać tabelę częstotliwości, dane są uporządkowane od najmniej do największej i informują, ile danych odpowiada każdej kategorii, która będzie kwalifikacją, którą uczeń uzyska w temacie fizyki:

1.- Bardzo biedny: 4 studentów.

2.- Biedne: 6 studentów.

3.- Wystarczy: 20 studentów.

4.- Cóż: 17 studentów.

5.- Doskonałe: 5 studentów.

Poniżej znajduje się histogram ocen, zbudowany z poprzedniej tabeli:

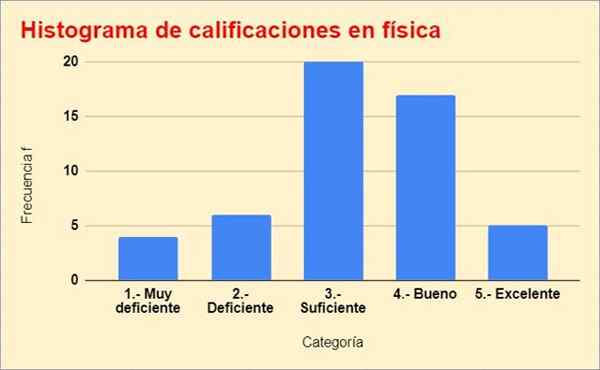Rysunek 2. Wykres rozkładu częstotliwości ćwiczenia rozwiązane. Źródło: f. Zapata.

Bibliografia

1. Berenson, m. 1985. Statystyka administracji i ekonomii. Inter -American s.DO.
2. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
3. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
4. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
5. Spiegel, m. 2009. Statystyka. Seria Schaum. 4 Ta. Wydanie. McGraw Hill.
6. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.