Koncepcja relacji proporcjonalności, przykłady i ćwiczenia

Relacje proporcjonalne Są to powiązania między dwiema lub więcej zmiennymi, tak że gdy jedna z kwot jest różna, podobnie jak wartość pozostałych. Na przykład, jeśli ktoś wzrośnie, inne mogą zwiększyć lub zmniejszyć, ale w jednolitym ilości.

Starożytni greccy matematycy zdali sobie sprawę, że niektóre zmienne były powiązane w bardzo precyzyjny sposób. Zdali sobie sprawę, że jeśli okrąg ma dwa razy więcej niż inna, będzie miało okrąg o podwójnej długości.

Rysunek 1. Długość koła jest wprost proporcjonalna do jego średnicy D. Źródło: f. Zapata

A jeśli potrójnie średnica, wówczas kontur obwodu również potroi. Oznacza to, że wzrost średnicy powoduje proporcjonalny wzrost wielkości obwodu.

I dlatego możemy potwierdzić, że długość obwodu l jest proporcjonalna do jego średnicy D, która jest wyrażona w następujący sposób:

L ∝ d

Gdzie czytany jest symbol ∝bezpośrednio proporcjonalne do". Aby zmienić symbol proporcjonalności dla równości i uwzględnić wartości numeryczne, konieczne jest określenie związku między zmiennymi, zwanymi stała proporcjonalności.

Po dokonaniu wielu pomiarów starożytni matematycy ustalili, że stała proporcjonalności między wielkością L obwodu a jego średnicą D wynosiła numer 3.1416… Punkty zawiesinowe wskazują nieskończoną liczbę dziesiętnych.

Ta wartość jest niczym innym jak słynną liczbą π (pi) i w ten sposób piszemy:

L = π.D

W ten sposób przyczyna między długością a średnicą koła jest taka sama jak przyczyna między długością a średnicą innej. A najlepsze jest to, że mamy teraz sposób na obliczenie długości dowolnego obwodu, znając jego średnicę.

[TOC]

Przykłady relacji proporcjonalności

W nauce (a także w życiu codziennym) bardzo ważne jest znalezienie relacji między zmiennymi, aby wiedzieć, w jaki sposób zmiany w jednym z nich wpływają na drugie. Na przykład:

Może ci służyć: ile średnich ma obwód?

-Jeśli zrobić tuzin ciastek, potrzebne są 3 mąki. Ile kubków jest potrzebnych do zrobienia 2 i pół tuziny?.

-Wiedząc, że na planecie Merkury obiekt waży 4 razy mniej niż na Ziemi, ile 1 samochód w rtęci.5 ton?

-W jaki sposób zmiana siły zastosowana w przyspieszeniu ciała, na której ma zastosowanie?

-Jeśli pojazd porusza się z jednolitym ruchem prostoliniowym na autostradzie i wiemy, że podróżuje 30 km w 10 minut, jaka będzie odległość przebywająca po 20 minutach?

-Kiedy mamy drut, przez który przechodzi prąd elektryczny, w jaki sposób napięcie między jego końcami różni się, jeśli wzrasta?

-Jeśli średnica koła jest podwojona, jak wpływa to twój obszar?

-W jaki sposób odległość do intensywności pola elektrycznego wytwarzanego przez punktualny obciążenie?

Odpowiedź jest w zależnościach proporcjonalności, ale nie wszystkie relacje są tym samym typem. Następnie znajdziemy je na wszystkie poruszone tutaj sytuacje.

Bezpośrednia proporcjonalność i odwrotna proporcjonalność

Dwie zmienne x i y są w bezpośrednim proporcji, jeśli są powiązane przez:

y = kx

Gdzie k jest stałą proporcjonalności. Przykładem jest związek między ilościami mąki i plików cookie. Jeśli wykresujemy te zmienne, linia prosta jest uzyskiwana jako ta pokazana na rysunku:

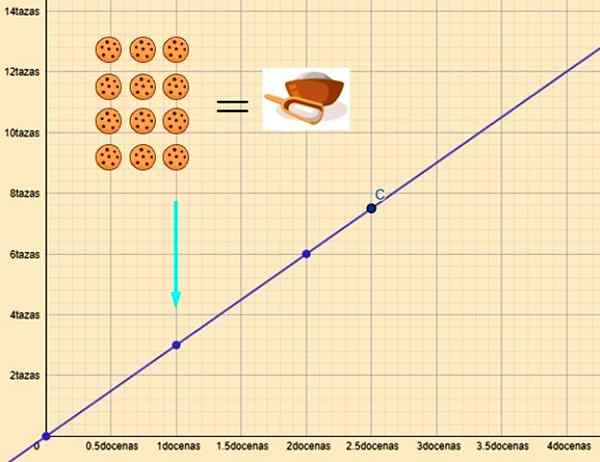Rysunek 2. Zrobić 2.5 tuzina ciasteczek potrzebuje 7.5 kubków mąki (punkt C). Źródło: f. Zapata.

Tak i są miseczkami mąki i x dziesiątki ciasteczek, związek między nimi jest:

y = 3x

Dla x = 1 tuzin potrzebujemy y = 3 szklanki mąki. I dla x = 2.5 tuzinów, y = 7 jest wymagane.5 miseczek.

Może ci służyć: 8 rodzajów błędów pomiarowych (z przykładami)

Ale mamy też:

-Przyśpieszenie Do To doświadcza ciała jest proporcjonalne do siły F To działa na niego, będąc masą ciała, nazywana M, Stała proporcjonalności:

F = mDo

Dlatego im większa siła przyłożona, tym większe wytworzone przyspieszenie.

-W przewodach omowych napięcie v między jego końcami jest proporcjonalne do prądu przyłożonego i. Stała proporcjonalności jest oporem kierowcy:

V = ri

-Gdy obiekt porusza się z jednolitym ruchem prostoliniowym, odległość D jest proporcjonalny do czasu T, bycie prędkością v Stała proporcjonalności:

d = v.T

Czasami znajdujemy dwie ilości, tak że wzrost w a zmniejszenie proporcjonalne w drugim. Ta jednostka nazywa się Odwrotna proporcja.

Na przykład w poprzednim równaniu czas T wymagany do przebycia określonej odległości d, jest odwrotnie proporcjonalny do prędkości V trasy:

T = d/v

I tym większa prędkość v, tym mniej czasu samochod. Jeśli na przykład prędkość jest podwojona, czas jest skrócony o połowę.

Gdy dwie zmienne x i y są w odwrotnej proporcji, możemy napisać:

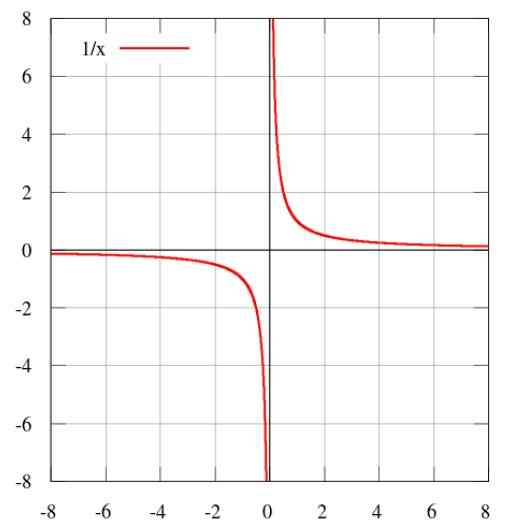
y = k / x

Będąc stałą proporcjonalności. Wykres tego urządzenia to:

Rysunek 3. Wykres 1/x reprezentujący odwrotną proporcjonalność. Źródło: Wikimedia Commons.

Inne rodzaje proporcjonalności

W jednym z wymienionych wcześniej przykładów zadaliśmy sobie pytanie, co stanie się z obszarem okręgu, gdy promień wzrośnie. Odpowiedź jest taka, że ​​obszar jest bezpośrednio proporcjonalny do kwadratu promienia, a proporcjonalność stała π:

A = πr²

W przypadku podwojenia promienia obszar wzrośnie o czynnik 4.

Aw przypadku pola elektrycznego I wytwarzane przez punktualne obciążenie Q, Wiadomo, że intensywność maleje wraz z odwrotnością do kwadratu odległości R do obciążenia Q:

E = k_I Q/r²

Może ci służyć: dlaczego algebra jest ważna w niektórych codziennych sytuacjach?

Ale możemy również potwierdzić, że intensywność pola jest bezpośrednio proporcjonalna do wielkości obciążenia, będąc stałą proporcjonalności k_I, Stała elektrostatyczna.

Innymi proporcjonalnością, które występują również w nauce, to proporcjonalność wykładnicza i proporcjonalność logarytmiczna. W pierwszym przypadku zmienne x i y są powiązane przez:

y = k.Do^X

Gdzie A jest podstawą, dodatnią liczbą 0, która zwykle wynosi 10 lub liczba E. Na przykład wykładniczy wzrost bakterii ma tę formę.

W drugim przypadku związek między zmiennymi wynosi:

y = k.dziennik_Do X

Ponownie a jest podstawą logarytmu, który często wynosi 10 (logarytm dziesiętny) lub e (logarytm neperiański).

Ćwiczenia

- Ćwiczenie 1

Wiedząc, że na planecie Merkury obiekt waży 4 razy mniej niż na Ziemi, jak bardzo 1 samochód w rtęci.5 ton?

Rozwiązanie  

Waga rtęci = (1/4) waga w ziemi = (1/4) x 1.5 ton = 0.375 ton.

- Ćwiczenie 2

Na przyjęcie niektórzy przyjaciele postanawiają przygotować sok z owocowych koncentratów. Instrukcje opakowania mówią, że 15 szklanek soku jest wykonanych ze szklanki koncentratu. Ile koncentratu jest potrzebne do zrobienia 110 szklanek soku?

Rozwiązanie

Niech i ilość naczyń soku i X ilość naczyń koncentratu. Są powiązane przez:

y = kx

Podczas wymiany wartości y = 15 i x = 1, stała k jest wyczyszczona:

K = y/x = 15/1 = 15

Dlatego:

110 = 15 x

x = 110/15 = 7.33 szklanki koncentratu owoców.

Bibliografia

1. Baldor, a. 1974. Algebra. Wenezuelski kulturalny s.DO.
2. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
3. Varsity Tutorrs. Relacje proporcjonalne. Źródło: WarsityTorm.com
4. Wikipedia. Proporcjonalność. Odzyskane z: jest.Wikipedia.org.
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.