Formuła zasad Simpsona, demonstracja, przykłady, ćwiczenia

Zasada Simpsona Jest to metoda obliczania w przybliżeniu zdefiniowanych całek. Opiera się na podzieleniu interwału integracji na parę pod-intervalów w równym stopniu rozmieszczonym.

Ekstremalne wartości dwóch kolejnych pod-intervalów definiują trzy punkty, co dostosowuje parabolę, której równanie jest wielomianem drugiego stopnia. 

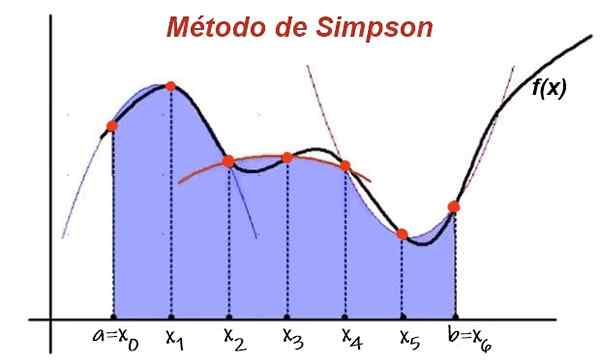
Rysunek 1. W metodzie Simpsona przedział integracji jest podzielony na parę odstępów o równej szerokości. Funkcja jest przybliżona przez przypowieść na każde 2 pod-intervalo, a podejście całkowe przez sumę obszaru pod przypowieściami. Źródło: UPV.Jest.

Następnie obszar pod krzywą funkcji w dwóch kolejnych odstępach jest przybliżony przez obszar wielomianowy interpolacji. Dodając wkład w obszar pod przypowieść o wszystkich kolejnych pod-interfejsach, istnieje przybliżona wartość całki.

Z drugiej strony, ponieważ całkę przypowieści można dokładnie obliczyć algebraicznie, można znaleźć formułę analityczną dla przybliżonej wartości zdefiniowanej całki. Jest znany jako Formuła Simpsona.

Błąd przybliżonego wyniku uzyskany w ten sposób zmniejsza się w zakresie, w jakim liczba podziałów n jest większa (będąc n momentem obrotowym).

Poniżej wyrażenia zostanie podane, które pozwala na oszacowanie górnego poziomu błędu podejścia do całki I, gdy partycja regularnych podinterwali całkowitego przedziału [A, B] została wykonana [B].

[TOC]

Formuła

Interwał integracji [a, b] jest podzielony na n podnapi, a n jest momentem obrotowym. Szerokość każdego podziału będzie:

H = (B - a)/n

W ten sposób, w przedziale [a, b] partycja jest tworzona:

X0, x1, x2, ..., xn-1, xn

Będąc x0 = a, x1 = x0 + h, x2 = x0 + 2h,…, xn-1 = x0 + (n-1) h, xn = x0 + nh = b.

Może ci służyć: różnica między okrągiem a obwodem (z przykładami)

Wzór, który umożliwia w przybliżeniu obliczenie określonej funkcji całkowej i ciągłej, a najlepiej miękka w przedziale [a, b] wynosi:

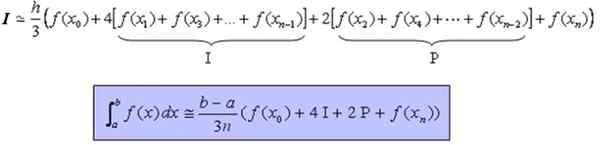
Demonstracja

To obtain the Simpson formula, in each subinterval [XI, XI+2] the function f (x) approaches by a second degree P (x) polynomial (parable) that passes through the three points: [xi, f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f xi)]; [Xi+1, f (xi+1)] i [xi+2, f (xi+2)]]].

Wówczas integralny wielomian P (x) jest obliczany w [XI, XI+2], który przybliża całkę funkcji F (x) w tym przedziale.

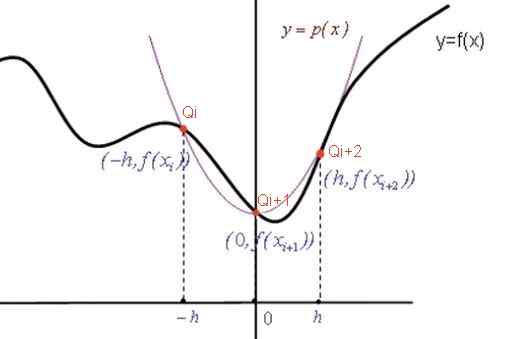Rysunek 2. Wykres wykazać formułę Simpsona. Źródło: f. Zapata.

Interpolacja współczynników wielomianowych

Równanie Parabola p (x) ma formę ogólną: p (x) = a x² + B x + c. Gdy przypowieść przechodzi przez punkty wskazane na czerwono (patrz rysunek), wówczas współczynniki a, b, c są określane na podstawie następującego układu równań:

A (-h)² - B H + C = F (xi)

C = f (xi+1)

A (h)² + B H + C = F (XI + 2)

Można zaobserwować, że współczynnik C jest określany. Aby określić współczynnik, dodajemy pierwsze i trzecie równanie:

2 a h² + 2 c = f (xi) + f (xi + 2).

Następnie wartość C jest zastąpiona i jest jasne:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 h²)

Aby określić współczynnik B, trzecie równanie pierwszego jest odejmowane, a B sama:

B = [f (xi+2) - f (xi)] = 2 h.

Podsumowując, wielomianowy drugiego stopnia P (x) przechodzi przez punkty Qi, Qi+1 i Qi+2, ma współczynniki:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 h²)

B = [f (xi+2) - f (xi)] = 2 h

C = f (xi+1)

Obliczenie przybliżonej całki w [XI, XI+2]

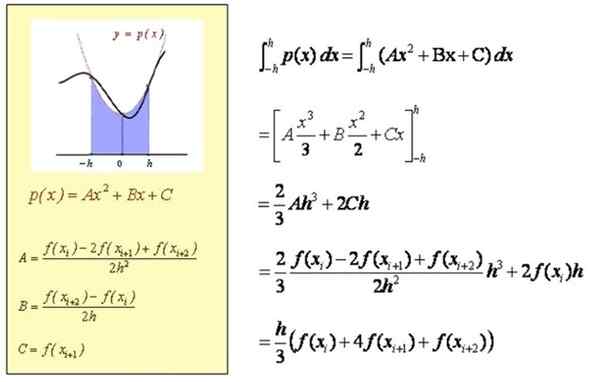
Przybliżone obliczenie całki w [a, b]

Jak już powiedziano, w całkowitym przedziale integracji [a, b] partycja x0, x1, x2,…, xn -1, xn ze krokiem h = xi+1 - xi = (b - (b -) / n, gdzie n jest parą.

Może ci służyć: Błąd próbkowania: wzory i równania, obliczenia, przykłady

Następnie całka zdefiniowana w całkowity odstęp [a, b] jest sumą całek w podintervalach [xi, xi+2], do których podchodzą całki wielomianów interpolacji p (x):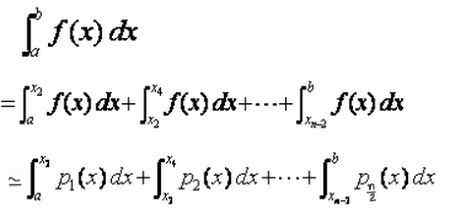

W poprzedniej sekcji znaleziono wzór dla całek wielomianowych w podinterwach. Zastosowanie tego wyniku do każdej integralnej ma: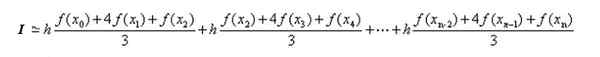

Które można przepisać w bardziej kompaktowy sposób w następujący sposób: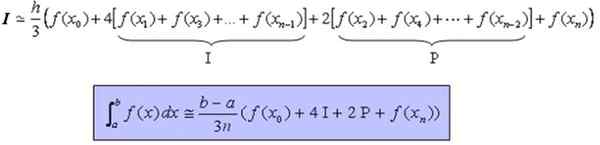

Błąd podejścia

Jeśli funkcja, do której chcesz zintegrować się z przedziałem [a, b], wyprowadziła się do czwartej rzędu, ciągła w tym przedziale, to możliwe jest znalezienie formuły, która pozwala określić maksymalny poziom błędu w podejściu za pomocą środków z Formuła Simpson Sn Dla wartości całki: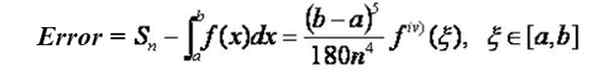

Należy zauważyć, że błąd zmniejsza się wraz z czwartą mocą liczby podziałów przedziałów. Na przykład, jeśli przejdziesz od N podzierzeń do 2N, błąd zmniejsza się o współczynnik 1/16.

Górny poziom błędu uzyskany przez podejście Simpsona można uzyskać z tego samego wzoru, zastępując czwartą pochodną maksymalną wartością bezwzględną czwartej pochodnej w przedziale [A, B].

Rozwiązane przykłady

- Przykład 1

Rozważ funkcję f (x) = 1 / (1 + x²). 

Znajdź zdefiniowaną całkę funkcji F (x) w przedziale [-1, 1] przy użyciu metody Simpsona z dwoma poddziałami (n = 2).

Rozwiązanie 

Jest zajęty n = 2. Limity integracji to A = -1 i B = -2, wówczas partycja jest taka: 

X0 = -1; X1 = 0 i x2 = +1.

Dlatego formuła Simpsona przyjmuje następująco:

Z n = 2 → xo = -1, x1 = 0; x2 = 1, dlatego:

- Przykład 2

Rozważ funkcję f (x) = 1 / (1 + x²). 

Znajdź zdefiniowaną całkę funkcji f (x) w przedziale [-1, 1] według wzoru Simpsona z czterema poddziałami (n = 4).

Może ci służyć: oszacowanie według interwałów

Rozwiązanie 

Jest zajęty n = 4. Limity integracji to A = -1 i B = -2, wówczas partycja jest taka: 

X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 i x4 = +1.

Formuła Simpsona jest ustalana w następujący sposób:

Integral ≃ [(b -a)/(3 n)] [f (x0) + 4 i + 2 p + f (xn)]

W przypadku, w którym jest stosowany, jest to następujące:

Integral ≃ (1- (1))/(3⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)

Integral ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1,5666

- Przykład 3

Określ zdefiniowaną całkę poprzednich przykładów dokładnie i dokonaj porównania dokładnego wyniku z wynikami uzyskanymi przez formułę Simpsona w przykładach 1a i 1b.

Rozwiązanie 

Nieokreślona całka funkcji f (x) = 1 / (1 + x²) to funkcja Arctan (x).

Podczas oceny limitów integracji:

Integral = arcTan (1) - arctan (-1) = π/4 - (-π/4) = π/2 = 1 5708

Jeśli porównamy wynik dokładnego rozwiązania z tym uzyskanym metodą Simpsona z n = 2 i n = 4, mamy:

Dla n = 2 różnica między dokładnym a przybliżonym rozwiązaniem wynosi π/2 -5/3 = -0959, to znaczy różnica procentowa wynosząca -0,06%.

A dla podejścia Simpsona z n = 4 różnica między dokładnym a przybliżonym rozwiązaniem wynosi π/2 - 47/30 = 0,0041, to znaczy różnica procentowa 0,003%.

Proponowane ćwiczenie

Metoda Simpsona jest odpowiednia do stosowania w językach programowania i aplikacjach komputerowych skierowanych do obliczeń matematycznych. Jest proponowany czytelnikowi, który na podstawie formuł podanych w tym artykule napisz swój własny kod w swoim ulubionym programie.

Poniższy rysunek pokazuje ćwiczenie, w którym formuła Simpsona została zaimplementowana Studio Smath, Bezpłatne oprogramowanie dostępne dla systemów operacyjnych Okna I Android.

Rysunek 3. Przykład integracji numerycznej za pośrednictwem reguły Simpsona za pomocą oprogramowania. Źródło: f. Zapata.

Bibliografia

1. Casteleiro, J. M. 2002. Kompleksowe obliczenia (wydanie ilustrowane). Madryt: ESIC Editorial.
2. UPV. Metoda Simpsona. Polytechnic University of Valencia. Odzyskane z: YouTube.com
3. Purcell, e. 2007. Obliczenie dziewiątej edycji. Prentice Hall.
4. Wikipedia. Zasada Simpsona. Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Interpolacja wielomianowa Lagrange. Odzyskane z: jest.Wikipedia.com