Pierwiastek kwadratowy 3 (łatwe rozwiązanie i wyjaśnienie)

Korzeń kwadratowy 3 to 1,73205080756887.

Można to wyrazić:

√3 = 1,73205080756887

Wiedzieć, co to jest 3 pierwiastek kwadratowy, Ważne jest, aby poznać definicję pierwiastka kwadratowego liczby. Biorąc pod uwagę liczbę dodatnią „A”, pierwiastek kwadratowy „A”, oznaczony przez √A, jest liczbą dodatnią „B”, tak że gdy „B” jest przez nią mnożony, wynikiem jest „A”.

Definicja matematyczna mówi: √A = B tak, i tylko jeśli, B² = B*B = a. Dlatego, aby wiedzieć, jaki jest pierwiastek kwadratowy 3, to znaczy wartość √3, należy znaleźć liczbę „b”, że b² = b*b = √3.

Ponadto √3 jest liczbą irracjonalną, która składa się z nieskończonej nieodprawnej ilości dziesiętnych. Z tego powodu trudno jest obliczyć pierwiastek kwadratowy 3 ręcznie.

3 pierwiastek kwadratowy

Jeśli używany jest kalkulator, można zauważyć, że pierwiastek kwadratowy 3 to 1,73205080756887…

Teraz możesz ręcznie spróbować przybliżyć ten numer w następujący sposób:

-1*1 = 1 i 2*2 = 4, to mówi, że pierwiastek kwadratowy 3 to liczba między 1 a 2.

-1,7*1,7 = 2,89 i 1,8*1,8 = 3,24, dlatego pierwsza liczba dziesiętna wynosi 7.

-1,73*1,73 = 2,99 i 1,74*1,74 = 3,02, więc druga liczba dziesiętna wynosi 3.

-1 732*1 732 = 2,99 i 1733*1 733 = 3 003, dlatego trzecia liczba dziesiętna wynosi 2.

I tak dalej możesz kontynuować. Jest to ręczny sposób obliczania pierwiastka kwadratowego 3.

Istnieją również inne znacznie bardziej zaawansowane techniki, takie jak metoda Newton-Raphson, która jest metodą numeryczną do obliczania przybliżeń.

Gdzie możemy znaleźć liczbę √3?

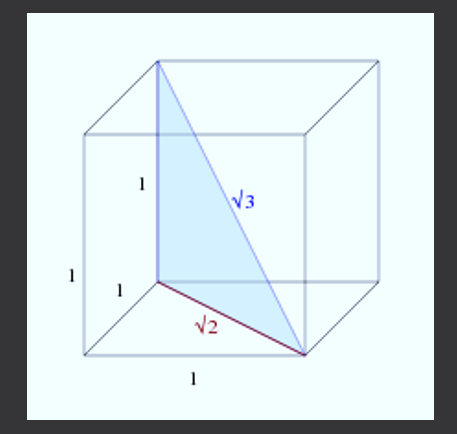
Ze względu na skomplikowaną liczbę można by pomyśleć, że nie pojawia się w obiektach codziennych, ale jest to fałszywe. Jeśli masz kostkę (kwadratowe), tak że długość jego boków wynosi 1, wówczas przekątna kostki będzie miała miarę √3.

Aby to zweryfikować, używane jest twierdzenie Pitagorasa, które mówi: Daj.

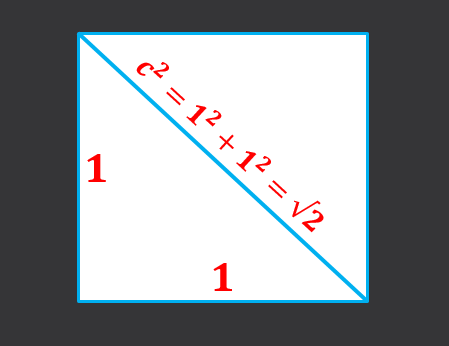
Mając stronę boku 1, musisz przekątna kwadrat jej podstawy jest równa suma kwadratów kategorii, to znaczy, c² = 1²+1² = 2, a zatem przekątna pomiaru podstawowego √2.

Teraz, aby obliczyć przekątę kostki, możesz zobaczyć poniższy rysunek.

Nowy trójkąt prostokąta ma nogi o długości 1 i √2, dlatego przy użyciu twierdzenia Pitagorasa do obliczenia długości jego przekątnej jest uzyskiwane: c² = 1²+(√2) ² = 1+2 = 3, mówi się, że mówi się , C = √3.

Zatem długość przekątnej wiadra bocznego 1 jest równa √3.

√3 liczba irracjonalna

Na początku powiedziano, że √3 jest liczbą irracjonalną. Aby to zweryfikować, przyjmuje to absurdalność, która jest liczbą racjonalną, której istnieją dwie liczby „A” i „B”, względni kuzyni, takie jak A/B = √3.

Gdy ostatnia równość i jasna „A²”, uzyskano następujące równanie: A² = 3*B². To mówi, że „A²” to wielokrotność 3, co stwierdza, że ​​„A” jest wielokrotnością 3.

Będąc „wielokrotnością” 3, istnieje liczba całkowita „k” taka, że ​​a = 3*k. Dlatego przez zastąpienie w drugim równaniu uzyskuje się: (3*k) ² = 9*k² = 3*b², co jest takie samo jak B² = 3*k².

Tak jak poprzednio, ta ostatnia równość prowadzi do wniosku, że „B” jest wielokrotnością 3.

Podsumowując, „A” i „B” są wielokrotnościami 3, co jest sprzecznością, ponieważ na początku założono, że były one względnymi kuzynami.

Dlatego √3 jest liczbą irracjonalną.