Jaki jest związek między rombem a obszarem prostokąta?

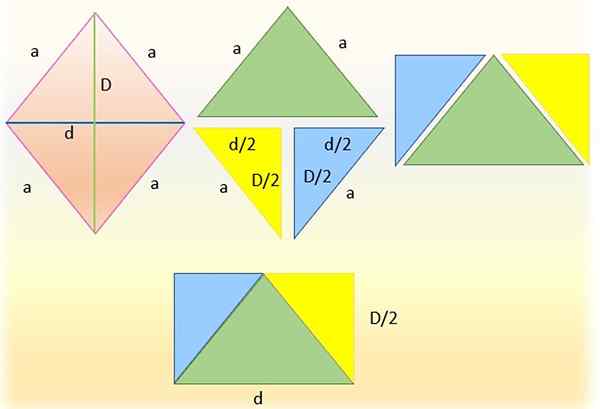
Rozkładając romb, aby uzyskać prostokąt. Źródło: f. Zapata

Możliwe jest obliczenie obszaru rombowego (i niektórych innych liczb geometrycznych) na powierzchni trójkąta lub powiązanego czworoboku, takiego jak równoległobok lub prostokąt.

Prostokąt i obszar równoległoboku jest taki sam: jest obliczany jako produkt między podstawą figury a jej wysokością w odniesieniu do tej podstawy. Ze swojej strony obszar trójkąta jest półproduktem między jej podstawą a wysokością.

Formuły te są łatwe do zapamiętania, chociaż oczywiście geometria oferuje wyłączną formułę dla obszaru Rombusa, znając miarę jego głównych i mniejszych przekąt, oznaczonych odpowiednio jako D i D:

Możliwe jest wydukanie tego wyrażenia poprzez sekwencję pokazaną na powyższym rysunku.

Aby to zrobić, romb po lewej jest przecięty przez jedną z jego przekątnych, co zostało wykonane na odcinku figury przez mniejszą przekątkę, otrzymując w ten sposób dwa trójkąty. Górny trójkąt (w kolorze zielonym) jest pozostawiony, a dolny podzielony jest z kolei na dwa trójkąty, przecinane na połowę głównej przekątnej, uzyskując prostokąty trójkątów identycznie niebieski i żółty.

Następnie hipotencje tych trójkątów pokrywają się z bokami zielonego trójkąta, ponieważ mierzą to samo, czyli „a”. I ostatecznie uzyskuje się prostokąt, którego podstawa jest dolna „D” po przekątnej i której wysokość wynosi połowę głównej przekątnej, to znaczy: „D/2”.

W ten sposób utworzony obszar prostokąta pokrywa się dokładnie z rombą, dlatego można potwierdzić, że:

Może ci służyć: trójmian

DO _diament = (podstawa × wysokość) _prostokąt = D × (d/2)

Wynik, że, jak widać, zbiega się dokładnie z formułą obszaru rombowego podanego wcześniej.

Rombo i obszar równoległoboku

Obszar rombowy jest również związany z obszarem równoległoboku, ponieważ obie postacie geometryczne są płaskie i należą do rodziny czworoboku. Na przykład na poniższym obrazie jest romb po lewej stronie i równoległobok po prawej stronie.

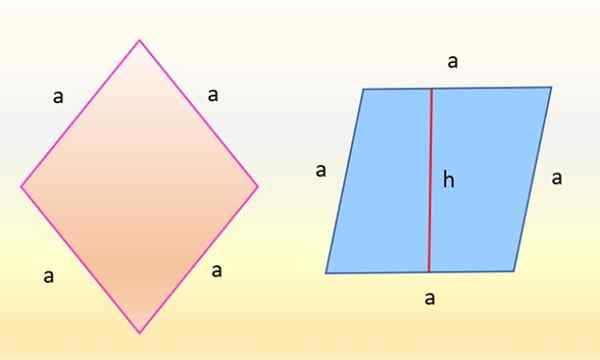Obszar rombowy po lewej jest taki sam jak obszar równoległoboku po prawej stronie. Źródło: f. Zapata

Okazuje się, że liczby są identyczne, ponieważ zmieniło się tylko orientacja. Romb po lewej, w kolorze różowym, którego boki mają tę samą miarę: a, jest odwracany w taki sposób, że jedna z jego stron jest całkowicie pozioma. Następnie romb przybiera kształt niebieskiego równoległoboku po prawej stronie.

A obszar tego równoległoboku jest również produktem między podstawą „A” a wysokością w odniesieniu do tej podstawy, zwanej „H” na rysunku, dlatego:

DO _{równoległobok} = A × H

Ponieważ jest to ta sama liczba, obszar jest identyczny i następuje:

DO _diament = A × H

Zatem, wiedząc i H równoległoboku, jego powierzchnia jest obliczana i będzie się pokryć z obszarem romb.

Obszar Rombo wpisany w prostokąt

Kolejny związek między rombem a prostokątem pojawia się, gdy pierwszy jest zarejestrowany w drugim. Jeśli tak się stanie, wierzchołki rombu pokrywają się z punktem środkowym boków prostokąta, który pokazano poniżej:

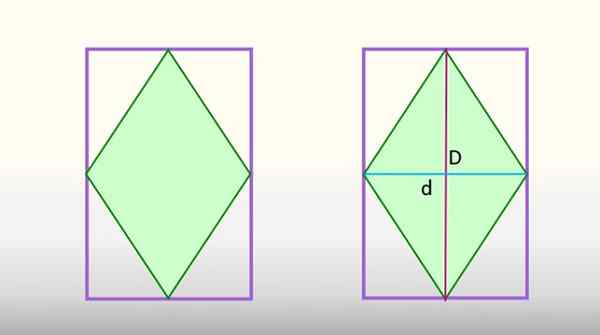Obszar rombowy wpisany w prostokącie jest równoważny połowy obszaru prostokąta. Źródło: f. Zapata

Przepis ten czyni główną i mniejszą przekątną romb, figura jest podzielona na 8 identycznych trójkątów, z których 4 odpowiadają rombowi, w kolorze zielonym, a pozostałe 4 są częścią prostokąta. Gdyby te ostatnie 4 trójkąty połączą się, utworzyłyby połowę prostokąta, a 4 trójkąty rombowe, drugie.

Może ci służyć: trójkąt Isosceles

Dlatego obszar Rombusa jest równoważny połowy obszaru prostokąta, w którym jest zarejestrowany, stwierdzając, że:

DO_diament = A_prostokąt / 2

Można to łatwo zweryfikować poprzez obliczenie obszaru jednego z trójkątów i mnożenie przez 4, ponieważ są one identyczne. Obszar dowolnego trójkąta to połowa produktu między podstawą a jego wysokością:

DO _trójkąt = podstawa × wysokość /2

Z poprzedniej figury zaobserwowano, że podstawą jednego z trójkątów jest d/2, a wysokość jest d/2, co wymiana w poprzednim wzorze daje:

DO _trójkąt = (d /2) × (d /2) /2 = (d × d) /8

Mnożenie tego wyniku przez 4, aby mieć obszar Rhombus:

DO _diament = 4 (d × d) /8 = (d × d) /2

Ze swojej strony połowa prostokąta to:

DO _prostokąt / 2 = podstawa × wysokość / 2

Ponieważ podstawa prostokąta jest D, a jego wysokość jest D, pozostaje:

DO_prostokąt / 2 = D × D/ 2

Który jest dokładnie obszarem zarejestrowanego romb. Stwierdzono zatem, że:

Obszar romb zarejestrowany w prostokącie jest równoważny połowy obszaru tego.

Rozwiązane ćwiczenia

Ćwiczenie 1

Ile kosztuje obszar rombowy, którego główne przekątne mierzy 14.6 cm i dolna przekątna 9.8 cm?

Rozwiązanie

Zastępując D = 14.6 cm i d = 9.8 cm w formule obszaru Rhombus:

Poszukiwany obszar to:

DO _diament = 14.6 cm × 9.8 cm = 143.1 cm²

Ćwiczenie 2

Na rysunku poprzedniej sekcji główna przekątna romb zarejestrowana w prostokącie mierzy d = 30 cm, a obszar prostokąta jest wart 210 cm². Poproszono o obliczenie:

a) Długość mniejszej przekątnej

Może ci służyć: segment linii i półiany

b) Obszar Rombusa na dwa sposoby: pierwszy przez obszar prostokąta, a drugi przy użyciu wzoru obszaru romb. Sprawdź, czy wynik jest taki sam.

Rozwiązanie

Obszar prostokąta to produkt między jego podstawą a wysokością. Największa przekątna jest jego wysokość, podczas gdy podstawa byłaby najmniejsza. Korzystając z formuły obszaru i zastępując wartości instrukcji, masz:

DO _prostokąt = podstawa × wysokość = d × 30 cm = 210 cm²

Wtedy baza jest warta:

D = 210 cm² / 30 cm = 7 cm

Rozwiązanie b

Jak widać powyżej, obszar Rhombus jest połowa obszaru prostokąta i wiadomo:

DO _diament = 210 cm² /2 = 105 cm²

Wynik jest sprawdzany natychmiast, zastępując formułę:

Piagonals są już znane: D = 30 cm, D = 7 cm, następnie:

DO _diament = 30 cm × 7 cm /2 = 105 cm²

Udowodniono, że zgodnie z oczekiwaniami obszar rombowy jest taki sam w obu przypadkach.