Testowanie hipotez

Co to jest test hipotez?

testowanie hipotez, W statystykach jest to procedura stosowana w celu sprawdzenia, jak skuteczna jest domniemanie o populacja. Te przypuszczenia są nazywane hipoteza, że w zasadzie są uważane za prawdziwe, dopóki pewne dowody potwierdzają lub odmówi.

Dowody te są dostarczane przez dane przykładowe, które pochodzą ze znacznej części populacji, zwanej próbka. Teoria prawdopodobieństwa stanowi niezbędne techniki kontrastowania prawdziwości hipotez.

Przykłady hipotez to:

-Średnia temperatura ludzkiego ciała wynosi 36.1 ºC.

-Średnio słona torba orzechowa wyprodukowana w fabryce przekąsek waży 50 g.

-80% mieszkańców miasta dokonało zakupów online w ciągu ostatnich 6 miesięcy.

-Wyniki testu IQ dla studentów uniwersytetów ze znanej instytucji, ma standardowe odchylenie wynoszące 15.

-Pewna zmienna losowa x jest zgodna z rozkładem Poissona.

Pierwsze cztery są typem hipotezy parametryczny, ponieważ są to stwierdzenia dotyczące pewnego parametru populacji, takich jak średnia, odchylenie standardowe lub pewna proporcja.

Z drugiej strony ostatnia hipoteza określa rozkład zmiennej losowej, a ponieważ nie odnosi się do żadnego parametru ani właściwości populacji, mówi się, że jest to hipoteza nie parametryczny.

Hipoteza zerowa i alternatywna hipoteza

Istnieją dwa rodzaje hipotez, z którymi można wykonać test, który posłuży na ich kontrast:

-Hipoteza zerowa, oznaczone jako h₀, stwierdza, że ​​badany parametr ma ustaloną wartość lub że zmienna losowa jest zgodna z określonym rozkładem. Dlatego, symbolicznie wyrażając hipotezę zerową, zawsze używany jest symbol równości.

-Alternatywna hipoteza: nazywany h₁, Potwierdza, że ​​parametr lub rozkład różnią się od tego, co zapewnia hipoteza zerowa, stąd symbolicznie wyrażać alternatywną hipotezę, używane są symbole: lub ≠, ale nigdy nie równość.

Może ci służyć: własność Algebra Lock: Demonstration, przykłady

Po zaakceptowaniu hipotezy zerowej, alternatywna hipoteza jest odrzucana, tak że oba są wzajemnie wykluczające się.

Poziom istotności

Jest to miara błędu, którą można popełnić podczas przeprowadzania testu hipotez. Jest zdefiniowany jako prawdopodobieństwo odrzucenia hipotezy zerowej, ponieważ to prawda. Zazwyczaj jest to oznaczone grecką literą α:

α = p (odrzucaj h₀ Kiedy to prawda)

Wartości powszechnie stosowane dla α wynoszą 0.01, 0.05 i 0.10; Bycie drugim najczęstszym użyciem. Odpowiednik odpowiednio do 1%, 5% i 10% prawdopodobieństwa popełnienia błędów po odrzuceniu h₀, Ale w każdym razie im niższy poziom istotności, tym bardziej niezawodny wynik testu.

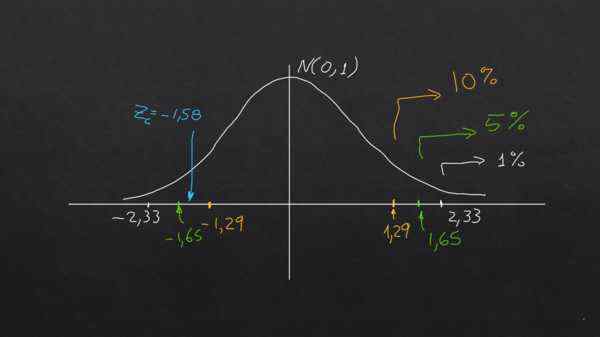
Wartość alfa (α) można rozumieć jako procentową frakcję prawego ogona (lub lewy), w rozkładu normalnym (μ = 0 i σ = 1) i wartości te zawsze występują przy z = 2,33 dla α = 0.01; przy z = 1,65 dla α = 1,65 i przy z = 1,29 dla α = 0,1.

Kroki wykonania testu hipotez

Krok 1

Zdefiniuj odpowiednio hipotezy zerowe i alternatywne. Hipoteza zerowa określa, że ​​badany parametr, zwany θ, jest równy wartości odniesienia, oznaczonej jako θ₀:

H₀: θ = θ₀

Na przykład, jeśli wpływ leku jest badany na pewną cechę populacji myszy laboratoryjnych, hipoteza zerowa zastanawia się, że ten lek nie robi żadnej różnicy w takiej cechy i że ma on stałą wartość θ₀.

Aby symbolizować hipotezę zerową, z drugiej strony znak równości jest zawsze używany.

W przykładzie leku alternatywna hipoteza określa, że ​​związek ma pewien wpływ na cechę dana. Dlatego jest to większe, niższe lub po prostu inne niż wartość odniesienia θ₀.

Może ci służyć: notacja czynnikowa: koncepcja, przykłady i ćwiczenia

Krok 2

Wybierz odpowiedni poziom istotności, który zwykle ustalono na poziomie 5 %, jak wcześniej wskazano.

Krok 3

Określ populację i ekstrakt z niej próbkę lub próbki, których analiza będzie służyć do kontrastowania hipotez i określenie akceptacji lub odrzucenia hipotezy zerowej.

Krok 4

Wybierz i oblicz wartość statystyki próbnej dla zebranych danych, z których uzyskano niezbędne dowody w celu podjęcia decyzji o przyjęciu lub odrzuceniu hipotezy zerowej. Wybór statystyki próbnej zależy od wybranego parametru: średniej, odchylenia, proporcji lub innej.

Statystyka próbna uzyskuje się przez przekształcenie parametru próbki na wynik Z, statystykę Student, Pearson lub Chi Square, zgodnie z wybranym projektem eksperymentalnym. Są do tego formuły.

Zwykle, jeśli parametr populacji jest średnim μ, „x słupek” jest średnią próbką, odchylenie standardowe σ jest znane, a wielkość próbki wynosi n> 30, statystyka testowa z_C Oblicza się go z wynikiem Z:

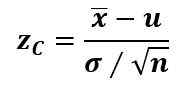
A kiedy n < 30, pero σ es desconocida, se usa la t de Student.

Krok 5

Ustal kryteria przyjęcia lub odrzucenia hipotezy zerowej, które można wykonać za pomocą dwóch procedur:

• Poprzez wartości p.
• W porównaniu z wartościami krytycznymi.

Wartości p są równoważne z prawdopodobieństwem uzyskania znalezionych wyników, ponieważ hipoteza zerowa jest prawdziwa. Jeśli wartości te są małe, hipoteza zerowa jest odrzucona, jeśli nie są, jest akceptowana. W każdym razie wartości p nie stanowią dowodu, że alternatywna hipoteza jest prawdziwa.

Należy wziąć pod uwagę, że w teście hipotezy można wykonać dwa rodzaje błędów:

• Błąd typu I: Odrzuć h₀ Kiedy to prawda. Jego prawdopodobieństwo jest α i jest równoważne z poziomem istotności dowodu.
• Błąd typu II: Zaakceptuj h₀ Kiedy to jest fałszywe. Jego prawdopodobieństwo jest oznaczone jako β.

Może ci służyć: jaki jest związek między obszarem Rhombusa a prostokątem?

Krok 6

Podejmij decyzję o przyjęciu lub odrzuceniu hipotezy zerowej. Jeśli używane są wartości p, gdy p < α, se rechaza H₀ I h jest akceptowane₁, I w przeciwnym razie H jest akceptowane₀. Zestaw wartości p < α se conoce como region krytyczny. Jeśli statystyka jest w tym przedziale, H jest odrzucane₀.

Podobnie wybrana jest wartość krytyczna, zgodnie z wybranym parametrem populacji. Jeśli jest to średnia, postępuj w następujący sposób:

• Test ogona: θ < θ₀ lub θ> θ₀
• Test dwa ogony: | θ | < θ₀

Rozwiązany przykład

Maszyna produkuje śruby, których wartość nominalna musi mieć 800 milimetrów długości, przy standardowym odchyleniu 5%.

Przyjmuje się losową próbkę, to znaczy w różnych dniach tygodnia produkcyjnego, który wynosi około 40 śrub. Po obliczaniu średniej długości próbki uzyskuje się wartość 790 milimetrów.

Określ, czy średnia długość jest tolerancja z poziomem istotności odpowiednio 1%, 5% i 10%.

Rozwiązanie

Pierwszym z nich jest obliczenie średniej statystyki testowej, która w tym przypadku jest odchyleniem średniej podzielonej między standardowym błędem populacji:

ZC = (790 - 800) / (40 / √40) = -1,58

Gdzie uwzględniono, że odchylenie standardowe 5% odpowiada 40 z 800.

Hipoteza zerowa polega na tym, że średnia próbka mieści się w ramach tolerancji dozwolonej do wymaganego poziomu istotności, pod warunkiem, że | zc | jest mniej niż typowa wartość | zt |, w przeciwnym razie hipoteza zerowa jest odrzucona.

Dla istotności 1% i 5% hipoteza zerowa jest spełniona, ponieważ | ZC | < 2,33 y |Zc| < 1,65 respectivamente.

Jednak dla 10% znaczenia zdarza się, że | Zc | > 1.29. To znaczy na tym poziomie istotności hipoteza zerowa nie jest spełniona.

Poniższy wykres wyjaśnia wniosek:

Wykres pokazuje, że w zależności od poziomu istotności wymaganej tej samej hipotezy można zaakceptować lub odrzucić za pomocą tych samych danych. Źródło: f. Zapata.