Oszacowanie według przedziałów

Jakie jest oszacowanie według interwałów?

Oszacowanie według przedziałów Jest to sposób na określenie zakresu wartości, w których można uwzględnić średnią populacji, na podstawie informacji o próbce o skończonej wielkości, losowo wyodrębnionej z całkowitej populacji.

On Interwał szacunkowy Jest niższy, ponieważ próbka jest większa, ale staje się szerszy, jeśli poziom lub procent niezawodności tych samych wzrośnie.

Jeśli chcesz znać średnią populacji pewnej zmiennej w dokładnej formie, należy wziąć pod uwagę całkowitą populację, coś, co nie zawsze jest wykonalne, ponieważ jeśli jest to bardzo duża populacja, uzyskanie danych z danych z danych jest drogie Cała populacja. Z tego powodu do przyjmowania jest jedna lub więcej losowych próbek całkowitej populacji.

Opiera się na hipotezie, że wydobywając losową próbkę, nie jest stronnicza i biorąc pod uwagę proporcjonalnie wszystkie warstwy, wówczas średnia wartość próbki musi być bardzo zbliżona do średniej populacji.

Logika wskazuje, że im większe dane próbki, różnica między średnią wartością próbki a średnią wartością populacji jest niższa.

Interwał szacunkowy

W praktyce, chyba że pełna populacja jest znana, możliwe jest znalezienie jedynie prawdopodobieństwa, przedziału, w którym można znaleźć średnią populacji, na podstawie próbki wielkości skończonej.

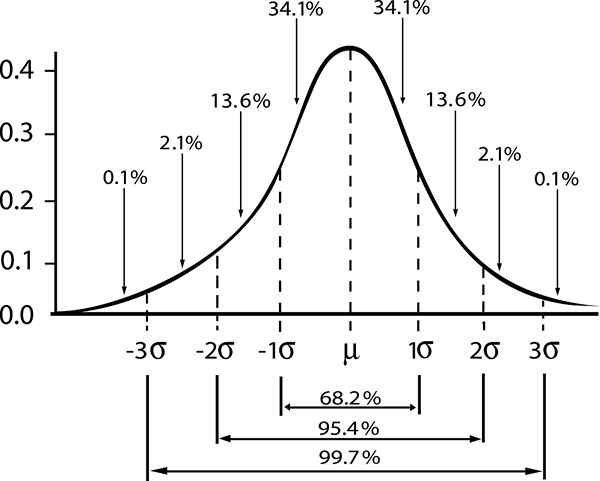
W przypadku populacji, która następuje po rozkładowi normalnym Odchylenie standardowe σ , Standardowa różnica Między średnią populacji μ i średnia próbka wielkości N jest dany przez:

| μ - | ≤ σ / √n

Tutaj słowo „standard” wskazuje, że 68% próbek wielkości N, Mają średnią wartość między przedziałem [μ - σ / √n, μ + σ / √n].

Może ci służyć: kryteria podziału: czym one są, jakie są użycie i zasady

Standardowe oszacowanie

Alternatywną interpretacją powyższego byłoby stwierdzenie, że średnia populacji uzyskana z próby wielkości N a średnia wartość jest rozumiana w przedziale  [ - σ / √n, + σ / √n], Z 68% prawdopodobieństwem.

W większości rzeczywistych przypadków nie można znać standardowego odchylenia populacji, więc σ Jest przybliżony przez odchylenie standardowe próbki S, który jest obliczany w następujący sposób:

S = √ (∑ (x_Siema - )² / √ (n-1).

Stamtąd otrzymujesz interwał, który może zawierać średnią populacji z poziomem ufności 68% (standardowy poziom ufności), podany przez:

  -s / √n ≤ μ ≤ + s / √n

Ten przedział pomiaru populacji jest znany jako standardowy przedział szacunkowy i uzyskano tylko z danymi dostępnymi pod względem wielkości N.

Z poprzedniej formuły wynika z tego, że jeśli chcesz wzmocnić interwał szacunkowy w połowie, konieczne jest to poczwórny Rozmiar próbki.

Oszacowanie według przedziałów ufności

W niektórych badaniach standardowy poziom 68% może być niewystarczający, wówczas konieczne jest określenie interwałów o dowolnym poziomie ufności γ.

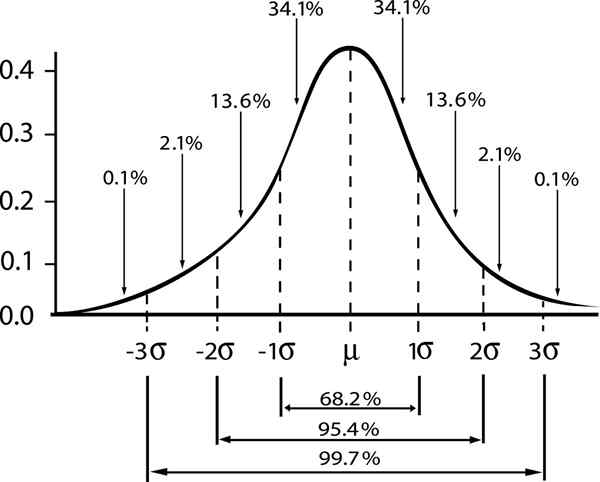Pokazano związek między marginesem niezawodności a przedziałem w rozmieszczeniu Gaussa

Jeśli oznaczamy przez ε Błąd standardowy s/√n, Następnie błąd oszacowania poziomu ufności γ zostanie podany przez:

E = Zγ⋅ε.

Gdzie Zγ Jest to liczba, według której błąd standardowy jest mnożony, a tym samym uzyskuje margines błędu z dowolnym poziomem ufności γ.

Aby uzyskać czynnik Zγ, postępować w następujący sposób:

Może ci służyć: liczby racjonalne: właściwości, przykłady i operacje

Krok 1

To połączenie poziom istotności α odpowiadający poziomowi zaufania γ według następującej formuły:

α = 1 - γ

Krok 2

Wartość jest określana:

Jest to częstotliwość skumulowana w rozkładu normalnym N (0,1) W przedziale (-lu, Zγ ].

Krok 3

To oczyszcza Zγ Równanie:

N (zγ) = 1 - α/2

Ponieważ jest to równanie integralne, ten klirens uzyskuje się z tabel rozkładu normalnego, przy użyciu liniowej metody interpolacji.

Krok 4

Alternatywnie dla użycia tabel, funkcje statystyczne włączone do arkuszy kalkulacyjnych, takich jak Przewyższać, albo Arkusz Google. Programy te zawierają normalną funkcję odwrotną N^-1, tak, że współczynnik korekcji Zγ Uzyskuje się bezpośrednio oceniając tę ​​funkcję odwrotną:

Zγ = n^-1(1 - α/2).

Typowe przedziały zaufania

Najczęściej stosowane poziomy ufności to:

• Zγ = 1; Standardowy poziom ufności γ = 0,68.
• Zγ = 2; poziom zaufania γ = 0,95 (lub poziom istotności 5%).
• Zγ = 3; poziom zaufania γ = 0,997 (lub 0,3%poziom istotności)

Przykłady

Przykład 1

Określ średni odstęp masy noworodków w sierpniu w dużym mieście oparty na losowej próbce 100 niemowląt, w którym uzyskano średnią wagę 3100 gramów z próbką odchylenia standardowego S = 1500 gramów.

Rozwiązanie

Po pierwsze, standardowy błąd próbki jest określany:

ε = s/√n = (1500 g)/√100 = 150 g.

Dlatego, zaczynając od tej próbki, można wywnioskować, że średnia waga dzieci urodzonych w sierpniu w tym mieście wynosi od 2950 g do 3250 g, z 68% prawdopodobieństwem.

Przykład 2

Załóżmy, że wielkość próbki dzieci urodzonych w tym samym miesiącu sierpnia i w tym samym mieście przykładu 1. Średnia masa próbki wynosi 3100 g przy standardowej dyspersji 1500 g. 

Może ci służyć: rozkład liczb naturalnych (przykłady i ćwiczenia)

Poproszono o oszacowanie średniego przedziału masy noworodków tego miasta, z tej nowej próbki.

Rozwiązanie

Teraz błąd standardowy maleje w współczynniku 1/√2, Tak więc nowy błąd standardowy średniej wagi wyniesie 106 g.

Następnie można oszacować na podstawie tej nowej próbki, że średnia waga noworodków składa się w zakresie od 2994 g do 3206 g, z prawdopodobieństwem 68%.

Ćwiczenia

Ćwiczenie 1

Określ średni zakres masy noworodków w sierpniu, zaczynając od próbki określonej w przykładzie 1, z prawdopodobieństwem 95%.

Rozwiązanie

95% poziom niezawodności podwaja średni zakres wagi, w porównaniu z poziomem niezawodności 68%.

Dlatego średnia waga noworodków jest uwzględniona w zakresie 2800 gramów przy 3400 gramach z 95% pewnością.

Ćwiczenie 2

Oszacuj przy 99,7% poziomu ufności przedział, w którym stwierdzono średnia waga noworodków z dużego miasta, jeśli próbka jest dostępna ze średnią wagą 100 niemowląt równych 3100 g, a ze standardowym odchyleniem próbki S = 1500 G.

Rozwiązanie

Średnia margines błędu masy, z 99,7% pewności, będzie potrójny średni błąd, to znaczy:

3*1500/√100.

Następnie z tej próbki wywnioskuje się, że średnia waga noworodków zostanie uwzględniona w przedziale: 2650 gramów do 3550 gramów, przy poziomie pewności 99,7%. 

Z tego wyniku obserwuje się, jak w przypadku większego poziomu pewności zwiększa niepewność średniej wagi do znacznie szerszego odstępu.