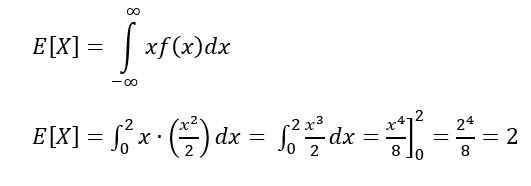Ciągła zmienna losowa

Wyjaśniamy, czym jest ciągła zmienna losowa, jej cechy, przykłady i rozwiązane ćwiczenie

Jaka jest ciągła zmienna losowa?

A Ciągła zmienna losowa Jest to wartość numeryczna uzyskana losowo, co wynika z przeprowadzenia eksperymentu i może przyjmować nieskończone wartości. Oznacza to, że znane dwie kolejne wartości zmiennej zawsze można znaleźć inną wartość pośredniej między nimi.

Posiadając nieskończoną ilość wartości, gromadzenie wartości zmiennych nie jest rachunkowym i prawie zawsze należy do zestawu liczb rzeczywistych.

Przykładami tego typu zmiennych są postawa, waga i temperatura ciała osoby, ale można zdefiniować niezliczone z nich, kilka przykładów zostanie znalezione poniżej. W przeciwieństwie do ciągłej zmiennej losowej istnieje dyskretna zmienna losowa, która jest rachunkowością, taka jak liczba córek w rodzinie lub ile samochodów sprzedaje agencję po jednym miesiącu.

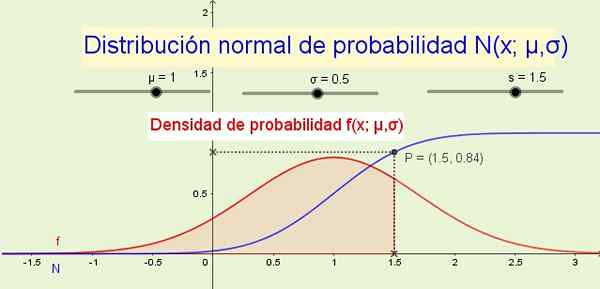
Dyskretne zmienne losowe często następują po normalnym rozkładowi prawdopodobieństwa. Źródło: f. Zapata.

Ciągła losowa zmienna jest oznaczona za pomocą litery kapitałowej, takiej jak X, a nieskończone wartości, które przyjmuje zmienna, są możliwymi wynikami losowego eksperymentu:

X = x₁, X₂, X₃,… ∞

Każda wartość ma pewne prawdopodobieństwo wystąpienia i do modelu, w którym obliczane jest to prawdopodobieństwo, jest wywoływane rozkład prawdopodobieństwa.

Ale ponieważ x przyjmuje nieskończone wartości, prawdopodobieństwa określonych wartości zmiennej nie można obliczyć. Konieczne jest zdefiniowanie funkcji f (x), zwanej Zgromadzona funkcja rozkładu, lub po prostu funkcja rozkładu, zgodnie z którą skumulowane prawdopodobieństwo jest obliczane do określonej wartości lub między dwiema wartościami:

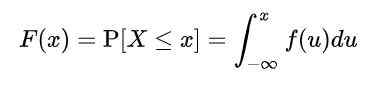
Gdzie f (u) otrzymać nazwę funkcja gęstości. Zdefiniowane w ten sposób, F (x) reprezentuje prawdopodobieństwo, że X jest pomiędzy -∞ i X.

Charakterystyka ciągłej losowej zmiennej

Ciągłe zmienne losowe są kompletne f (x).

Funkcja gęstości f (x) musi spełniać następujące nieruchomości:

• Funkcja f (x) To jest pozytywne: f (x)> = 0
• Obszar pod krzywą y = f (x) Zawsze jest równe 1, to znaczy, że prawdopodobieństwo wystąpienia pewnego wyniku X W przedziale (-∞, +∞) wynosi 100%.
• Prawdopodobieństwo, że x jest w przedziale [a, b], jest obliczane na podstawie następującej zdefiniowanej całki:

Może ci służyć: ograniczenie: definicja, typy, formuły, na przykład, na przykład

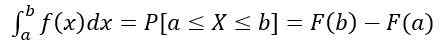
Który jest równoważny obszarowi pod krzywą y = f (x), rozumiane między Do I B. Oprócz:

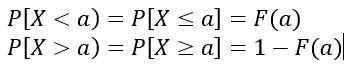
Wartości f (x) Nie reprezentują prawdopodobieństwa, więc P [x = c] = 0. Odpowiednie wartości to te odpowiadające obszarowi pod krzywą y = f (x), które reprezentują prawdopodobieństwo.

• Wyprowadzając funkcję rozkładu F (x) z szacunkiem do X, jest uzyskiwany f (x).

Wykres f (x) W przypadku ciągłej zmiennej losowej jest ona analogiczna do wielokąta częstotliwości zbudowanego dla dyskretnej zmiennej statystycznej, z różnicą, że dla zmiennej losowej szerokość przedziału staje się nieskończona.

Mieć nadzieję

Nadzieja jest jednym z charakterystycznych miar zmiennej ciągłej. Nadzieja lub oczekiwana wartość X Wskazuje wartość, która ma występować częściej i jest obliczana za pomocą następującej całki:

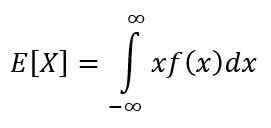
Jego właściwości to:

• E [a∙ x] = a∙ e [x]
• E [x + y] = e [x] + e [y]]
• E [a∙ x+b∙ y] = a∙ e [x] + b∙ e [y]

Gdzie kwoty Do I B To liczby rzeczywiste.

Przykłady

Jak wcześniej wskazano, istnieje wiele sytuacji, w których można zdefiniować jedną lub więcej ciągłych zmiennych losowych. W nauce i innych obszarach najczęstsze są czas, długość, waga, objętość i temperatura:

Czas

Aby zoptymalizować procesy i usługi, eksperymenty są zaprojektowane, które badają czas, który poświęcony jest:

X = czas, który zabiera klienta do okna bankowego.

Y = co zajmuje miejsce fast food w serwowaniu zamówienia.

Z = czas, w którym zachodzi pewna reakcja chemiczna.

Uzdlanki i ciężary

W wielu badaniach na temat ludzi i zwierząt istotne są statystyki i wagi:

X = wysokość dziewcząt na szóstym polu. Dyplom w każdej szkole w mieście.

Może ci służyć: zgodność: zgodne dane, kryteria, przykłady, ćwiczenia

Y = waga dzieci w urodzeniu w szpitalu publicznym.

Z = waga krów na farmie.

Temperatury

Temperatura jest odpowiednim parametrem w wielu procesach chemicznych, który zwykle przyjmuje nieskończone wartości w określonym zakresie:

X = temperatura, w której występuje pewna reakcja chemiczna, wiedząc, że występuje to między 80 ° C a 120 ° C.

Rozwiązane ćwiczenia

Ćwiczenie 1

Określ, jakie są ciągłe zmienne losowe:

1. Liczba studentów uczęszczających na kawę uniwersytecką.
2. Ciśnienie krwi pacjentów przychodzących na pogotowie.
3. Długość skrzydeł ptaków, zagrożonego gatunku, który zamieszkuje rezerwat.
4. Czas między jedną osobą a drugą jest traktowany w banku.
5. Ilość wadliwych produktów miesięcznie w fabryce.
6. Poziomy cholesterolu w kurczakach farmy.
7. Ilość lamp ulicznych na ulicy, łącznie 12.

Rozwiązanie

1.- Liczba uczniów uczestniczących w ciągu dnia jest zdrętwiała, dlatego ta zmienna nie jest ciągła, ale dyskretna.

2.- Jest ciągły. Ciśnienie krwi pacjentów może przybierać dowolną wartość w danym zakresie.

3.- Zmienna ciągła, ponieważ długość skrzydła ptaka ma dowolną wartość między minimum a maksimum, w zależności od gatunku.

4.- Czas między obsługą klienta jest zmienna i może przyjąć dowolną wartość w danym zakresie, na przykład od 1 do 5 minut.

5.- Ponieważ liczba wadliwych produktów jest rachunkowością, jest to dyskretna zmienna losowa.

6.- Ta zmienna jest ciągła, ponieważ poziom cholesterolu w kurczakach ma dowolną wartość w określonym zakresie.

Może ci służyć: uzupełniające się kąty: które i jak są one obliczane, przykłady, ćwiczenia

7.- Dyskretny. Liczba świateł oświetlenia, które działają.

Ćwiczenie 2

Ciągła zmienna losowa jest zdefiniowana X = "poziom cholesterolu " W pewnej różnorodności kurczaków farmy, która ma następującą funkcję gęstości f (x):

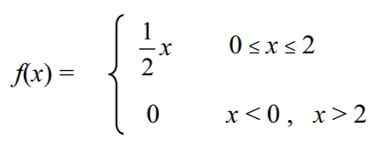
Oblicz następujące:

1. F (x)
2. P [x ≤2]
3. Nadzieja BYŁY]

Rozwiązanie

Zgodnie z definicją podaną na początku:

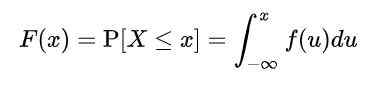
Dlatego, F (x) Jest to funkcja w części. Dla interwału X<0, F (x) Jest równy 0, dla właściwości określonych na początku.

W przedziale 0≤X≤2, Integra nieokreślona jest rozwiązana:

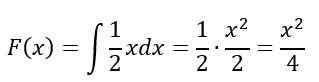
Wreszcie, w przedziale X> 2, F (x) = 1, Dlatego zgodnie z właściwościami, F (x) Pozostaje tak:

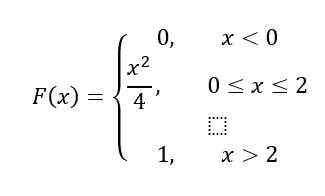
Rozwiązanie b

Poszukiwane prawdopodobieństwo jest F (1.2) i COmo x = 1.2 Znajdź to między 0≤X≤2, ta część F (x) Oceniać:

F (1.2) = ¼ ∙ (1.2)² = 0.36.

Rozwiązanie c

Aby obliczyć wartość nadziei lub oczekiwaną, jest ona używana: